Tổng hợp 80 bài tập trắc nghiệm luyện tập môn Toán Chuyên đề hàm số

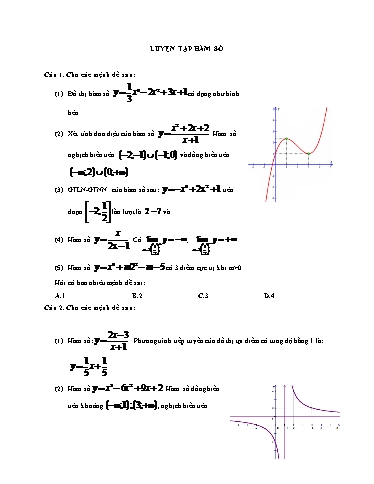
 LUYỆN TẬP HÀM SỐ
Câu 1. Cho các mệnh đề sau:
 1
 (1) Đồ thị hàm số y x3 2x2 3x 1có dạng như hình 
 3
 bên. 
 x2 2x 2
 (2) Xét tính đơn điệu của hàm số y . Hàm số 
 x 1
 nghịch biến trên 2; 1  1;0 và đồng biến trên 
 ;2  0; .
 (3) GTLN-GTNN của hàm số sau: y x4 2x2 1 trên 
 1 
 đoạn 2; lần lượt là 2 7 và .
 2 
 x
 (4) Hàm số y . Có lim y ; lim y 
 2x 1 1 1 
 x x 
 2 2 
 (5) Hàm số y x4 m22 m 5 có 3 điểm cực trị khi m>0.
 Hỏi có bao nhiêu mệnh đề sai: 
 A.1 B.2 C.3D.4
Câu 2. Cho các mệnh đề sau:
 2x 3
 (1) Hàm số: y . Phương trình tiếp tuyến của đồ thị tại điểm có tung độ bằng 1 là: 
 x 1
 1 1
 y x .
 5 5
 (2) Hàm số y x3 6x2 9x 2 . Hàm số đồng biến 
 trên khoảng ;1 ; 3; , nghịch biến trên 4 2
 (5) Hàm số y x 4x 3 đạt cực tiểu tại xct=0 đạt cực đại tại xcđ= 2 .
 Hỏi có bao nhiêu phát biểu đúng:
 A.2B.3C.5D.1
Câu 4. Cho các mệnh đề sau:
 (1) Hàm số y x3 6x2 9x 2 đồng biến trên ;1 ; 3; khoảng nghịch biến 
 trên khoảng 1;3 .
 (2) Hàm số y x4 x2 nghịch biến trên các khoảng a 1.
 (3) Hàm số y x không có cực trị.
 (4) Để phương trình x4 4x2 m 1 0 có đúng 2 nghiệm thì m<1 và m=5.
 x m
 (5) Hàm số y có tất cả 2 tiệm cận với mọi m.
 x2 1
 Có bao nhiêu mệnh đề đúng:
 A.2B.3C.4D.5
Câu 5. Cho các mệnh đề sau:
 (1) Hàm số y x3 3x2 4 có đồ thị như hình vẽ:
 3 2
 (2) Hàm số y f x x 3x 2016 có phương trình tiếp tuyến tại hoành độ x0 1 là
 y 9x 2011 . x 1
 (5) Cho hàm số y để hàm số đồng biến trên khoảng 2;2 thì tập giá trị đầy đủ 
 x m
 của m là: m>2.
 Có bao nhiêu mệnh đề đúng:
 A.1B.2C.3D.4
Câu 8. Cho các mệnh đề sau:
 (1) Hàm số y 2x3 6x2 5 . Có đồ thị như sau:
 x 1
 (2) Hàm số y có 1 tiệm cận đứng chỉ khi 
 x2 3x m
 9
 m .
 4
 (3) Hàm số trở thành y 2x4 4x2 3 nghịch biến trên 
 các khoảng ; 1 và 0;1 ; đồng biến trên các 
 khoảng 1;0 và 1; .
 (4) Hàm số y x4 4x2 3 (1). Có 2 điểm uốn.
 (5) Hàm số y 3 x C . Tiếp tuyến của C tại 
 2 5
 điểm có hoành độ x 1 là y x .
 3 3
 Có bao nhiêu mệnh đề đúng:
 A.1B.3
 C.4D.5
Câu 9. Cho các mệnh đề sau:
 (1) Cho y x3 3x2 4 (1). Hàm số có điểm 
 cực đại tại 0;4 , điểm cực tiểu tại 2;0 .
 (2) Đồ thị hàm số y 2x3 3x2 1 có đồ thị dạng:
 2x 2
 (3) Cho hàm số y giao điểm của 2 tiệm cận nằm trên đường thẳng y x .
 x 2 (2) Hàm số y x3 3x2 đồng biến trên các khoảng ;0  2; và nghịch biến 
 trên khoảng 0;2 .
 (3) Giá trị lớn nhất và nhỏ nhất của hàm số: y 2x3 3x2 12x 1 trên  1;5 lần 
 lượt là 266 và 1.
 1
 (4) Tiếp tuyến của đồ thị hàm số y x3 2x2 3x 1 mà song song với đường thẳng 
 3
 29
 y 3x 1 có phương trình là y 3x .
 3
 2x 3
 (5) Hàm số y có lim y ; lim y .
 x 1 x 1 x 1 
 Có bao nhiêu mệnh đề sai trong các mệnh đề trên?
 A.1B.2C.3D.4
Câu 12. Cho các mệnh đề sau:
 3x 2
 (1) Hàm số y có tiệm cận đứng là y 3 và tiệm cận ngang x 1.
 x 1
 (2) Hàm số y x4 2x2 có 2 điểm cực đại và 1 điểm cực tiểu.
 (3) Giá trị của m để đường thẳng y mx 1 cắt đồ thị C của hàm số 
 y x3 2x2 1 tại ba điểm phân biệt là 1; .
 x2 16
 (4) GTLN, GTNN của hàm số y trên đoạn 2;4 lần lượt là và 4.
 x 1 3
 x 2
 (5) Hàm số y có đồ thị C . Phương trình tiếp tuyến với đồ thị C tại điểm 
 x 1
 thuộc C có tung độ bằng 4 là y 3x 10 .
 Chọn số mệnh đề đúng trong các mệnh đề trên:
 A.1B.2C.3D.4
 ĐÁP ÁN VÀ LỜI GIẢI
Câu 1. Chọn C. 1
(1) Đúng. Vì với y 1 2x 3 x 1 x 4; y '(4) 
 5
 1 1 1
Phương trình tiếp tuyến tại điểm A(4;1) là: y (x 4) 1 x 
 5 5 5
(2) Sai. Vì hàm số y x3 6x2 9x 2 
Đồ thị hàm số có điểm cực đại xCD 1, đồ thị hàm số có điểm cực tiểu xCT 3là phát biểu không 
chuẩn, điểm cực đai, cực tiểu phải có kí hiệu như sau: điểm cực đại A(1;2) và điểm cực tiểu 
B(3;-2)
 x2 1
(3) Sai. Vì đường cong y có 2 tiệm cận ngang là y = 1 và y = -1 và một tiệm cận đứng 
 x
x = 0 do
 1 1
 1 1 
 x2 1 2 x2 1 2
 lim y lim y lim y x ;lim y lim y lim y x 1 
 x x x x 1 x x x x 1
(4) Đúng.
 2 1 1 5
(5) Sai. Vì giá trị lớn của hàm số f (x) x 4 x trên đoạn 2; . Là 
 2 2
 x
+ Ta có: f '(x) 1 
 4 x2
 1 
+ f '(0) 0 x 2 2; 
 2 
 1 1 15
+ Có f ( 2) 2; f 
 2 2
 1 15
Kết luận: max f (x) ; min f (x) 2
 1 1 
 2; 2 2; 
 2 2 Phân tích sai lầm:
(1) Sai do các em quan sát không kỹ, dạng đồ thị giống nhau, nhưng tiệm cận ngang lại khác 
nhau;
(2) Sai chủ yếu do tính toán thôi;
(3) Sai do các em không hiểu bản chất, vì hàm số phân thức bậc nhất trên bậc nhất thì chỉ đơn 
điệu ( đồng biến, nghịch biến ) trên mỗi khoang xác định chứ không phải trên cả tập xác định.
(4) Sai do dùng từ ngữ không chuẩn, chỉ có đồ thị hàm số mới có điểm uốn chứ hàm số thì không 
dùng từ “điểm”
Câu 4. Chọn B.
(1) Đúng: Hàm số y x3 6x2 9x 2 (1). Đồng biến trên khoảng ( ;1);(3; ) , nghịch 
biến trên khoảng (1;3)
 x 2
(2) Đúng. Hàm số y nghịch biến trên khoảng ( ;1) và (1; ) do ta có:
 x 1
 x 1 x 2 3
 y ' 0,x D
 (x 1)2 (x 1)2
(3) Sai. Do hàm số y x đạt cực tiểu tại x = 0.
 x,khi _ x 0 1,khi _ x 0
Theo định nghĩa f (x) x f '(x) 
 x,khi _ x 0 1,khi _ x 0
Tuy rằng hàm số không có đạo hàm tại x = 0 nhưng thỏa mãn điều kiện để hàm số có cực trị. Ta có: y ' f '(x) 3x2 6x 
 Với x0 1 y0 2020 và y '(x0 ) y '(1) 9 
 Khi đó tọa độ tiếp điểm là M(1; 2020)
 Vậy phương trình tiếp tuyến của (C) là y 9(x 1) 2020 hay y 9x 2011
(3) Đúng. Để hàm số y x3 (m 3)x2 (m2 2m)x 2 đạt cực đại tại x = 2 thì 
m 0,m 2, y ' 3x2 2(m 3)x (m2 2m); y '' 6x 2(m 3)
 y '(2) 0
 Hàm số đã cho đạt cực đại tại x 2 
 y ''(2) 0
 12 4(m 3) m2 2m 0 m2 2m 0
 12 2m 6 0 m 0
 m 0
 .Kết luận: Giá trị m cần tìm là m=0, m=2
 m 2
(4) Sai. Vì: Hàm số y x4 2x2 3 điểm cực tiểu, một điểm cực đại
(5) Sai. Vì: Điều kiện để hàm số y f (x) có cực trị khi hàm số y f (x) liên tục trên khoảng ( a; 
b) và y ' f '(x) đổi dấu tại x x0 thuộc (a;b).
Phân tích sai lầm:
(1) Sai. Do chủ quan không quán sát kỹ điểm cực tiểu cho sai.
(4) Sai. Vì tính toán
(5) Sai. Vì: không hiểu rõ bản chất vấn đề, điều kiện để hàm số có cực trị.
Câu 6. Chọn D.
 3x 2
(4) Đúng. Hàm số y có tiệm cận đứng là x = 2, tiệm cận ngang y = 3. Giới hạn, tiệm 
 x 2
cận:
 4 4 
 lim y lim 3 3;lim y lim 3 3
 x x x 2 x x x 2 
 4 4 
 lim y lim 3 ;lim y lim 3 
 x 2 x 2 x 2 x 2 x 2 x 2 
 Đồ thị có TCĐ: x = 2; TCN: y = 3 3
(1) Sai. Vì hàm số đạt cực tiểu khi x 
 2
(2) Sai. Vì dùng sai dấu hợp, lỗi này được nhấn mạnh nhiều lần, phải sửa là trên ( ;1) và
( 1; ). 
 4 2
(3) Sai. Vì có 3 tiếp tuyến thỏa mãn. Cụ thể như sau: Gọi M (x0 ; x0 2x0 ) (C) và d là tiếp 
tuyến của (C) tại điểm M.
 3 4 2
Phương trình của d: y (4x0 4x0 )(x x0 ) x0 2x0 
 x0 1
 3 4 2 2 
A(1; 1) d 1 y (4x0 4x0 )(1 x0 ) x0 2x0 (x0 1) (3x0 1)(x0 1) 0 1 
 x 
 0 3
Phương trình có 3 nghiệm nên có 3 tiếp tuyến thỏa mãn.
(4) Đúng. Vì: Ta có bảng biến thiên