Tài liệu ôn thi tốt nghiệp THPT - Chuyên đề 12: Thể tích khối đa diện đơn giản

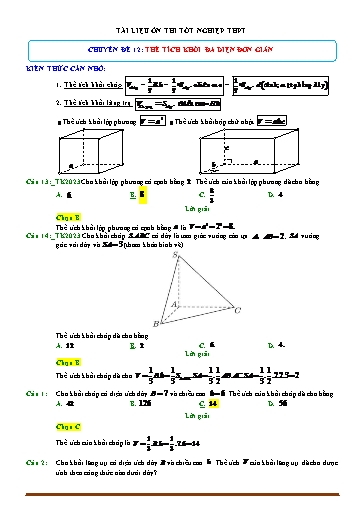
 TÀI LIỆU ÔN THI TỐT NGHIỆP THPT
 CHUYÊN ĐỀ 12: THỂ TÍCH KHỐI ĐA DIỆN ĐƠN GIẢN
KIẾN THỨC CẦN NHỚ:
 1 1 1
 1. Thể tích khối chóp V = B.h = ×S . chiÒu cao = ×S . d(đØnh; mÆt ph¼ng ®¸y)
 chãp 3 3 đ¸y 3 đ¸y
 2. Thể tích khối lăng trụ Vl¨ng trô = Sđ¸y . chiÒu cao=B.h
 3
 g Thể tích khối lập phương V = a g Thể tích khối hộp chữ nhật V = abc
 c
 a
 a b
Câu 13:_TK2023 Cho khối lập phương có cạnh bằng 2 . Thể tích của khối lập phương đã cho bằng
 8
 A. 6. B. 8 . C. . D. 4 .
 3
 Lời giải
 Chọn B
 Thể tích khối lập phương có cạnh bằng a là V a3 23 8.
Câu 14:_TK2023 Cho khối chóp S.ABC có đáy là tam giác vuông cân tại A , AB 2 ; SA vuông 
 góc với đáy và SA 3 (tham khảo hình vẽ).
 Thể tích khối chóp đã cho bằng
 A. 12. B. 2 . C. 6. D. 4.
 Lời giải
 Chọn B
 1 1 1 1 1 1
 Thể tích khối chóp đã cho V B.h S .SA . AB.AC.SA . .2.2.3 2 .
 3 3 ABC 3 2 3 2
Câu 1: Cho khối chóp có diện tích đáy B 7 và chiều cao h 6 . Thể tích của khối chóp đã cho bằng
 A. 42 . B. 126. C. 14. D. 56 .
 Lời giải
 Chọn C
 1 1
 Thể tích của khối chóp là V .B.h .7.6 14 .
 3 3
Câu 2: Cho khối lăng trụ có diện tích đáy B và chiều cao h . Thể tích V của khối lăng trụ đã cho được 
 tính theo công thức nào dưới đây? S
 C
 A
 B
 1
 Ta có BC 2 AB2 AC 2 suy ra ABC vuông tại A . S 24 , V S .SA 32
 ABC 3 ABC
Câu 9: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a . Biết SA  ABC và SA a 3 . 
 Tính thể tích khối chóp S.ABC .
 a a3 a3 3a3
 A. B. C. D. 
 4 2 4 4
 Lời giải
 Chọn C
 S
 a 3
 a
 A C
 a a
 B
 Ta có SA là đường cao hình chóp
 a2 3
 Tam giác ABC đều cạnh a nên S ABC 
 4
 1 a2 3 a3
 Vậy thể tích cần tìm là: V . .a 3 .
 S.ABC 3 4 4
Câu 10: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a . Cạnh bên SC vuông góc với mặt phẳng 
 ABC , SC a . Thể tích khối chóp S.ABC bằng
 a3 3 a3 2 a3 3 a3 3
 A. B. C. D. 
 3 12 9 12
 Lời giải
 Chọn D
 a2 3 1 a2 3 a3 3
 S V .a. .
 ABC 4 S.ABC 3 4 12 Câu 14: Cho khối chóp S.ABC có đáy ABC là tam giác vuông cân tại B , độ dài cạnh AB BC a , 
 cạnh bên SA vuông góc với đáy và SA 2a . Tính thể tích V của khối chóp S.ABC .
 a3 a3 a3
 A. V . B. V . C. V a3. D. V .
 3 2 6
 Lời giải
 S
 A C
 B
 Chọn A
 1 1 1 a3
 Ta có: V SA S 2a  a2 .
 S.ABC 3 ABC 3 2 3
Câu 15: Cho hình chóp S. ABC , có đáy ABC là tam giác vuông cân tại A , SA = AB = a , SA vuông 
 góc với mặt phẳng (ABC). Thể tích của khối chóp S. ABC bằng
 a3 a3 a3 3a3
 A. . B. . C. . D. .
 3 6 2 2
 Lời giải
 Chọn B
 1 a3
 Thể tích của khối chóp S. ABC : V = SA.S = .
 S.ABC 3 ABC 6
Câu 16: Cho tứ diện OABC có OA, OB, OC đôi một vuông góc và OA OB OC a . Khi đó thể tích 
 của tứ diện OABC là
 a3 a3 a3 a3
 A. . B. . C. . D. .
 12 6 3 2
 Lời giải
 Chọn B S
 3a
 A a B
 a
 D C
 2
 Diện tích đáy ABCD là SABCD a .
 Vì SA  ABC nên chiều cao của khối chóp là SA 3a .
 1 1
 Vậy thể tích khối chóp S.ABCD là: V .S .SA .a2.3a a3 .
 3 ABCD 3
Câu 20: Thể tích của khối chóp tứ giác đều có tất cả các cạnh bằng a là
 a3 2 a3 2 a3 2
 A. . B. . C. a3 . D. .
 6 3 2
 Lời giải
 S
 A
 B
 H
 D C
 Giả sử khối chóp tứ giác đều đã cho là S.ABCD . Khi đó ABCD là hình vuông cạnh a và 
 SA SB SC SD a .
 Gọi H là tâm của hình vuông ABCD thì SH  ABCD nên SH là chiều cao của khối chóp 
 S.ABCD . Tính SH :
 Xét tam giác ABC vuông tại B ta có: AC AB2 BC 2 a2 a2 a 2 .
 AC a
 Nhận thấy AC 2 SA2 SC 2 nên tam giác SAC vuông tại S . Suy ra SH .
 2 2
 2
 Diện tích đáy của khối chóp S.ABCD là SABCD a .
 1 1 a a3 2
 Vậy thể tích khối chóp S.ABCD là: V .S .SH .a2. .
 3 ABCD 3 2 6
Câu 21: Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng 2a . Tính thể tích 
 V của khối chóp S.ABC .
 11a3 11a3 13a3 11a3
 A. V B. V C. V D. V 
 6 4 12 12
 Lời giải
 Chọn D S
 A D
 I
 B C
 2
 a 2 a 14
 Chiều cao của khối chóp: 2 2 2 
 SI SA AI 4a 
 2 2
 1 1 a 14 14a3
 Thể tích khối chóp: V SI.S . a2 
 3 ABCD 3 2 6
Câu 24: Cho khối chóp tứ giác đều có cạnh đáy bằng 2a cạnh bên bằng a 5 . Thể tích của khối chóp đã 
 cho bằng
 4 5a3 4 3a3
 A. 4 5a3 . B. 4 3a3 . C. . D. .
 3 3
 Lời giải
 2 2 2 2 2
 Ta có SABCD 4a ; SO SB OB 5a 2a a 3
 1 a 3.4a2 4 3a3
 Vậy V SO.S 
 S.ABCD 3 ABCD 3 3
Câu 25: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a 6 , góc giữa cạnh bên và mặt đáy bằng 
 600 . Tính thể tích V của khối chóp S.ABC?
 A. V 9a3 B. V 2a3 C. V 3a3 D. V 6a3
 Lời giải
 Chọn D