Tài liệu ôn thi tốt nghiệp THPT - Chuyên đề 9: Nhận dạng đồ thị của hàm số và hệ số của biểu thức hàm số

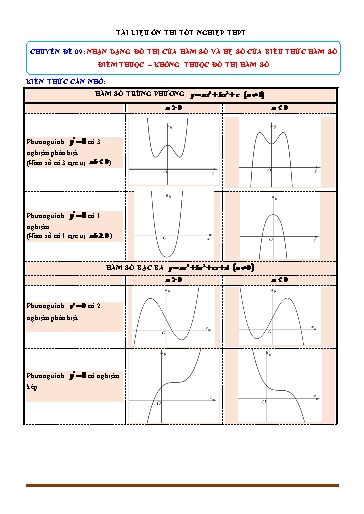
 TÀI LIỆU ÔN THI TỐT NGHIỆP THPT
 CHUYÊN ĐỀ 09: NHẬN DẠNG ĐỒ THỊ CỦA HÀM SỐ VÀ HỆ SỐ CỦA BIỂU THỨC HÀM SỐ
 ĐIỂM THUỘC – KHÔNG THUỘC ĐỒ THỊ HÀM SỐ
KIẾN THỨC CẦN NHỚ:
 HÀM SỐ TRÙNG PHƯƠNG y ax4 bx2 c a 0 
 a 0 a 0
Phương trình y 0 có 3 
nghiệm phân biệt
(Hàm số có 3 cực trị ab 0 )
Phương trình y 0 có 1 
nghiệm.
(Hàm số có 1 cực trị ab 0 )
 HÀM SỐ BẬC BA y ax3 bx2 cx d a 0 
 a 0 a 0
Phương trình y 0 có 2 
nghiệm phân biệt
Phương trình y 0 có nghiệm 
kép. DẠNG: XÉT DẤU CỦA CÁC HỆ SỐ HÀM SỐ THÔNG QUA ĐỒ THỊ
 BẢNG BIẾN THIÊN a : Dựa vào hướng đi lên, xuống của 
 ĐỒ THỊ HÀM SỐ “điểm cuối” đồ thị
 d : Dựa vào giao điểm của đồ thị với trục Oy
 c : Dựa vào cực trị
 b : Dựa vào cực trị
 a : Dựa vào (*)
 DẤU CÁC HỆ SỐ c : Dựa vào (**)
 b : Dựa vào cực trị
 Dựa vào giao điểm đồ thị và Ox → Dấu ab (1)
 Dựa vào TCN y = c/a → Dấu ac (2)
 Dựa vào giao điểm đồ thị và Oy → Dấu bd (3)
 Dựa vào TCĐ x = - d/c → Dấu dc (4)
Câu 9: _TK2023 Đồ thị hàm số nào dưới đây có dạng đường cong như hình bên
 x 3
 A. y x4 3x2 2 . B. y . C. y x2 4x 1. D. y x3 3x 5 .
 x 1
 Lời giải
 Đồ thị đã cho thuộc dạng đồ thị hàm phân thức hữa tỷ bậc nhất nên dễ dàng loại 3 đáp án A, C, 
 D (hàm đa thức).
Câu 1: ĐTK2022 Điểm nào dưới đây thuộc đồ thị của hàm số y x4 x2 2
 A. Điểm P( 1; 1) . B. Điểm N( 1; 2) . C. Điểm M ( 1;0) . D. Điểm Q( 1;1) .
 Lời giải Câu 7: Điểm nào dưới đây không thuộc đồ thị của hàm số y x4 x2 2
 A. Điểm P( 1; 2) . B. Điểm N(1; 2) . C. Điểm M ( 1;0) . D. Điểm Q(0; 2) .
 Lời giải
 Với x 1 y ( 1)4 ( 1)2 2 2 0 .
 x 3
Câu 8: Điểm nào dưới đây không thuộc đồ thị của hàm số y 
 x 1
 A. Điểm P(1; 1) . B. Điểm N(0; 3) . C. Điểm M (3;0) . D. Điểm Q( 2; 5) .
 Lời giải
 2 3
 Với x 2 y 5 .
 2 1
Câu 9: Điểm nào sau đây thuộc đồ thị hàm số y x4 mx3 mx 2019 ( m là tham số )?
 A. A 1;2020 . B. C 1;2019 .
 C. C 0;2020 . D. A 2;2020 .
 Lời giải
 +) Thay tọa độ điểm A 1;2020 vào hàm số y x4 mx3 mx 2019 ta được:
 1 4 m 1 3 m 1 2019 2020 2020 2020 luôn đúng với mọi giá trị của m .
Câu 10: Điểm nào sau đây thuộc đồ thị hàm số y x4 mx3 mx 2019 ( m là tham số ) và y x 2019
 với mọi giá trị của m ?
 A. A 1;2020 ; C 0;2019 . B. C 0;2019 .
 C. A 1;2020 ; B 1;2020 . D. A 1;2020 .
 Lời giải
 +) Thay tọa độ điểm C 0;2019 vào hàm số y x4 mx3 mx 2019 ta được:
 04 m.03 m.0 2019 2019 2019 2019 luôn đúng với mọi giá trị của m .
 +) Thay tọa độ điểm C 0;2019 vào hàm số y x 2019ta được: 
 2019 0 2019 2019 2019 luôn đúng với mọi giá trị của m .
 Từ đó loại đáp án C và đáp ánD.
 +) Thay tọa độ điểm A 1;2020 vào hàm số y x4 mx3 mx 2019 ta được:
 1 4 m 1 3 m 1 2019 2020 2020 2020 luôn đúng với mọi giá trị của m .
 +) Thay tọa độ điểm A 1;2020 vào hàm số y x 2019ta được: 
 2020 1 2019 2020 2020 luôn đúng với mọi giá trị của m .
 Vậy chọn đáp ánA.
 CÂU 7. (ĐTK2021) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. y x3 3x2 1. B. y x3 3x2 1.
 C. y x4 2x2 1. D. y x4 2x2 1.
 Lời giải
 Chọn C
 Từ hình có đây là hình dạng của đồ thị hàm bậc 4.
 lim f x lim f x a 0
 x x 
Câu 14: (Mã 104 2017) Đường cong hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó 
 là hàm số nào?
 A. y x3 3x 2 B. y x4 x2 1 C. y x4 x2 1 D. y x3 3x 2
 Lời giải
 Chọn D
 Đồ thị hình vẽ là đồ thị hàm số bậc ba có hệ số a 0 nên chỉ có hàm số y x3 3x 2 thỏa 
 mãn điều kiện trên.
Câu 15: (Mã 102 - 2020 Lần 2) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình 
 bên?
 A. y x4 2x2 1. B. y x4 2x2 1. C. y x3 3x2 1. D. y x3 3x2 1.
 Lời giải
 Chọn D x 1 x 2 x 2
A. y . B. y x2 2x . C. y . D. y .
 2x 2 2x 2x
 Lời giải
Chọn D
Dễ thấy đồ thị hàm số đã cho là đồ thị hàm số phân thức hữu tỉ nên loạiB.
Đồ thị hàm số nhận trục tung là trục đối xứng nên loại A.
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ âm nên loại đáp án C.
 x 2
Suy ra hàm số cần tìm là y .
 2x Câu 21: Đồ thị của hàm số nào dưới đây có dạng như đường cong hình dưới?
 A. y x3 3x2 . B. y x4 2x2 2 . C. y x4 2x2 2 . D. y x4 2
 Lời giải
 Chọn B
 Dễ thấy đồ thị hàm số đã cho là đồ thị hàm số bậc bốn trùng phương có hệ số a 0 (loại A).
 Mặt khác đồ thị hàm số cắt trục tung tại điểm có tung độ âm nên d 0 (loại C).
 Đồ thị hàm số có 3 điểm cực trị nên ab 0 .
 Suy ra hàm số cần tìm là y x4 2x2 2 .
 ax b
Câu 22: Cho hàm số y có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
 cx d
 A. ac 0,bd 0 . B. ab 0,cd 0 . C. bc 0,ad 0 . D. bc 0,ad 0 .
 Lời giải
 Chọn C
 d 
 Tập xác định D ¡ \ .
 c 
 d
 Do đường tiệm cận đứng của đồ thị hàm số là x nằm bên phải trục tung nên 
 c
 d
 0 cd 0 . 1 
 c
 a
 Do đường tiệm cận ngang của đồ thị hàm số là y nằm phía trên trục hoành nên
 c
 a
 0 ac 0 . 2 
 c Câu 24: Cho hàm số y ax3 bx2 cx d có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
 A. a 0,b 0,c 0,d 0 .B. a 0,b 0,c 0,d 0 .
 C. a 0,b 0,c 0,d 0 .D. a 0,b 0,c 0,d 0 .
 Lời giải
 Chọn C
 Đồ thị hàm số trên là đồ thị hàm số bậc ba có a 0 .
 Đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên d 0 .
 Có f x 3ax2 2bx c ;
 Hàm số có 2 điểm cực trị trong đó có 1 cực trị x1 0 và 1 cực trị x2 k với k 0 .
 Khi đó phương trình f x 0 có hai nghiệm phân biệt trong đó 1 nghiệm x1 0 và 1 nghiệm 
 x2 k với k 0 .
 Suy ra 3a.02 2b.0 c 0 c 0 .
 2b 2b
 Áp dụng định lý Vi-ét: x x . Có x x k 0 nên 0 mà a 0 nên b 0 .
 1 2 3a 1 2 3a
Câu 25: Cho hàm số y ax3 bx2 cx d có đồ thị như hình vẽ bên. Trong bốn số a,b,c,d có bao nhiêu 
 số âm?
 A. 3 . B. 1. C. 2 . D. 4 .
 Lời giải
 Chọn A
 Dễ thấy đồ thị hàm số đã cho là đồ thị hàm số bậc ba có hệ số a 0 .
 Đồ thị hàm số cắt trục hoành tại điểm có tung độ dương nên d 0 .
 Có f x 3ax2 2bx c ;
 Gọi x1, x2 là hai nghiệm của phương trình f x 0 . Khi đó x1 x2 0 và x1.x2 0 . c
 2
 b c
 Từ bảng biến thiên ta có: a b (1)
 a 2
 1
 b
 ac b
 Mặt khác: f ' x .
 bx c 2
 Vì hàm số đã cho đồng biến trên các khoảng ;2 và 2; nên
 ac b
 f ' x 0 ac b 0 (2)
 bx c 2
 c2 c
 Thay (1) vào (2), ta được: 0 c2 c 0 0 c 1.
 2 2
 Suy ra c là số dương và a, b là số âm.
Câu 28: (Mã 101 - 2020 Lần 1) Cho hàm số y ax3 bx2 cx d a,b,c,d ¡ có đồ thị là đường 
 cong trong hình bên. Có bao nhiêu số dương trong các số a , b , c , d ?
 A. 4 . B. 1. C. 2 . D. 3 .
 Lời giải
 Chọn C
 Ta có lim y a 0 .
 x 
 Gọi x1 , x2 là hoành độ hai điểm cực trị của hàm số suy ra x1 , x2 nghiệm phương trình 
 y 3ax2 2bx c 0 nên theo định lý Viet:
 2b b
 +) Tổng hai nghiệm x x 0 0 b 0 .
 1 2 3a a
 c
 +) Tích hai nghiệm x x 0 c 0 .
 1 2 3a
 Lại có đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên d 0 .
 Vậy có 2 số dương trong các số a , b , c , d .