Tài liệu ôn thi tốt nghiệp THPT - Chuyên đề 35: Tổng hợp tọa độ trong không gian (Mặt cầu) VD-VDC

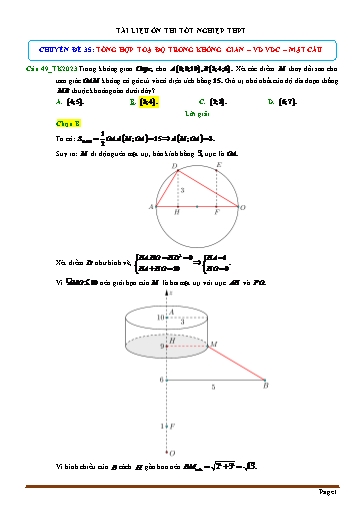
 TÀI LIỆU ÔN THI TỐT NGHIỆP THPT
 CHUYÊN ĐỀ 35: TỔNG HỢP TOẠ ĐỘ TRONG KHÔNG GIAN – VD VDC – MẶT CẦU
Câu 49_TK2023 Trong không gian Oxyz, cho A 0;0;10 , B 3;4;6 . Xét các điểm M thay đổi sao cho 
 tam giácOAM không có góc tù và có diện tích bằng 15. Giá trị nhỏ nhất của độ dài đoạn thẳng 
 MB thuộc khoảng nào dưới đây?
 A. 4;5 . B. 3;4 . C. 2;3 . D. 6;7 .
 Lời giải
 Chọn B
 1
 Ta có: S OA.d M ;OA 15 d M ;OA 3.
 OAM 2
 Suy ra: M di động trên mặt trụ, bán kính bằng 3, trục là OA.
 HA.HO HD2 9 HA 1
 Xét điểm D như hình vẽ, .
 HA HO 10 HO 9
 Vì ·AMO 90 nên giới hạn của M là hai mặt trụ với trục AH và FO.
 2 2
 Vì hình chiếu của B cách H gần hơn nên BM min 2 3 13.
 Page 1 Vì MA, MB, MC là 3 tiếp tuyến nên ta đặt MA MB MC x .
 VMAB có MA MB, ·AMB 60 nên MAB là tam giác đều, suy ra AB MA MB x .
 Áp dụng định lí Py-ta-go cho VMBC ta có BC MB2 MC2 2x2 x 2.
 Áp dụng định lí hàm số cos cho VMCA: CA MA2 MC2 2MA.MC.cos120 x 3.
 Nhận thấy AB2 BC 2 x2 2x2 3x2 AC 2 , suy ra VABC vuông tại B .
 Gọi I là tâm đường tròn ngoại tiếp VABC I là trung điểm của AC .
 Vì MA MB MC nên MI là trục đường tròn ngoại tiếp của VABC .
 Do đó M; I; E thẳng hàng.
 Mặt cầu S có tâm E 1;2; 3 bán kính R 3 3 EC
 EC
 Suy ra ME 6 . Vậy M thuộc mặt cầu S' có tâm E 1;2; 3 bán kính R ' 6 .
 sin 60 0
 Ta có OE 14
 Vậy MinOM OE R ' 6 14 .
Câu 3: Trong không gian với hệ trụcOxyz , cho mặt cầu (S): x 2 + y2 + z2 = 1 và hai điểm 
 A(3;0;0);B (- 1;1;0). Gọi M là điểm thuộc mặt cầu (S). Tính giá trị nhỏ nhất của biểu thức 
 MA + 3MB .
 A. 2 34 B. 26 C. 5 D. 34
 Lời giải
 FB Người gắn ID: Nguyễn Văn Toàn
 Chọn C
 Gọi M (x;y;z) là điểm cần tìm.
 Ta có : M Î (S) Þ x 2 + y2 + z2 - 1 = 0.
 2 2 2
 MA = (x - 3) + y2 + z2 ;MB = (x + 1) + (y - 1) + z2 .
 2 2 2
 Suy ra: MA + 3MB = (x - 3) + y2 + z2 + 3 (x + 1) + (y - 1) + z2
 2 2 2
 = (x - 3) + y2 + z2 + 8(x 2 + y2 + z2)- 8 + 3 (x + 1) + (y - 1) + z2
 Page 3 S có tâm I 2;1;1 ,bk R 2 .
IM 1 R điểm M nằm trong mặt cầu S và M nằm trên mặt cầu S tâm I,bk R 1
T MA 4MB đạt giá trị nhỏ nhất khi MB nhỏ nhất.
Vây minT 3 4.1 7 khi và chỉ khi AB là đường kính mặt cầu S AB 4 .
Cách 2: Gọi H là hình chiếu của I lên AB và đặt IH x 0 x 1 .
TH1: MA MB
Ta có T MA 4MB AH MH 4 MH HB 3MH 5AH 3 1 x2 5 4 x2 f x 
 3 5 
Ta có f x x 0 x 0 . Suy ra Tmin 13 khi d đi qua 
 1 x2 4 x2 
I AB 2R 4 .
TH2: MA MB
Tính được T 5 4 x2 3 1 x2 .
Xét hàm số f x 5 4 x2 3 1 x2 trên đoạn 0;1.
Tìm được min f x f 0 7 AB 4.
 0;1
 Page 5 B
 A M
 K
 H
 (Oxz) N
 A'
 Ta có H 1;0; 3 , K 2;0;1 lần lượt là hình chiếu vuông góc của A 1;1; 3 và B 2;3;1 
 xuống mặt phẳng Oxz .
 Nhận xét: A , B nằm về cùng một phía với mặt phẳng Oxz .
 Gọi A đối xứng với A qua Oxz , suy ra H là trung điểm đoạn AA nên AM A M .
 Mà A H AH 1; BK 3; HK 5 .
 Do đó AM BN A M BN HA 2 HM 2 BK 2 KN 2
 HA BK 2 HM KN 2 16 HM KN 2
 Lại có HM MN NK HK HM NK HK MN 5 2 3
 Dấu “=” xảy ra khi và chỉ khi H, M , N, K thẳng hàng và theo thứ tự đó.
 Suy ra AM BN 16 HM KN 2 16 3 2 5 .
 Vậy giá trị nhỏ nhất của AM BN bằng 5 .
Câu 8: Trong không gian Oxyz , cho ba điểm B 2;5;0 , C 4;7;0 và K 1;1;3 . Gọi Q là mặt phẳng 
 đi qua K và vuông góc với mặt phẳng Oxy . Khi 2d B, Q d C, Q đạt giá trị lớn nhất, 
 giao tuyến của Oxy và Q đi qua điểm nào trong các điểm sau đây?
 7 
 A. M 3;2;0 . B. N 15; 4;0 . C. P 8; 4;0 . D. Q 15; ;0 .
 2 
 Lời giải
 B,C Oxy 
 Gọi I là hình chiếu của K lên Oxy , suy ra I 1;1;0 
 qua K
 Q : suy ra, Q chứa IK
  Oxy 
 Gọi Oxy  Q qua I
 5 
 Gọi D là trung điểm của IC , suy ra D ,4,0 
 2 
 TH1: D,B cùng phía với 
 Page 7 qua I 1;1;0 
 Đường thẳng  5 7 : 5x 14y 19 0
 vtpt n AI ; ;0 
 4 2 
 Suy ra, N 15; 4;0 .
Câu 9: Trong không gian Oxyz , cho hai điểm A 1;2;3 và B 3;2;5 . Xét hai điểm M và N thay 
 đổi thuộc mặt phẳng Oxy sao cho MN 2023 . Tìm giá trị nhỏ nhất của AM BN .
 A. 2 17 . B. 65 . C. 25 97 . D. 205 97 .
 Lời giải
   
 Dựng véc tơ BB NM , khi đó BN MB , B Q qua B đồng thời song song với mặt phẳng 
 Oxy . Suy ra Q 5 .
 Vì BB MN 2023 suy ra B thuộc đường tròn tâm B , bán kính R 2023 nằm trong Q .
 Gọi A đối xứng với A qua Oxy , ta có A 1;2; 3 . Ta có AM BN A M MB A B .
 Gọi H 1;2;5 là hình chiếu vuông góc của A lên Q . Suy ra A H 8, HB 4 .
 Mặt khác HB HB BB 4 2023 2019
 Suy ra AM BN A B A H 2 HB 2 82 20192 205 97 .
Câu 10: Cho A 1;2;3 , B 2;3;4 . Mặt cầu S có bán kính R và S tiếp xúc với đồng thời cả ba mặt 
 phẳng Oxy,Oyz,Oxz . Khối cầu S chứa đoạn thẳng AB . Tính tổng các giá trị nguyên mà R 
 có thể nhận được?
 A. 7. B. 3 C. 1 D. 5
 Lời giải
 Vì mặt cầu S có bán kính R và S tiếp xúc với đồng thời cả ba mặt phẳng Oxy,Oyz,Oxz 
 nên tọa độ tâm I a,a,a và a R .
 Để khối cầu S chứa đoạn thẳng AB thì ta cần có:
 3 2 a 3 2
 IA2 R2 a2 6a 7 0 9 23
 a 3 2 .
 2 2 2 9 23 9 23
 IB R 2a 18a 29 0 a 2
 2 2
 Page 9 Khi đó a 1;0; 4 . 1;0;b 4 0 a 1 4b 16 0 a 4b 17 0 .
 17
 Vì a nguyên dương nên a 17 4b 0 b b 1;2;3;4 .
 4
 Các cặp a;b thỏa mãn là 13;1 , 9;2 , 5;3 , 1;4 .
Câu 13: Trong không gian Oxyz , cho 3 điểm A 0;0;1 , B 0;2;0 , C 3;0;0 . Gọi H , G lần lượt là trực 
 tâm, trọng tâm tam giác ABC . Viết phương trình mặt cầu tâm G và đi qua H .
 2 2 2 2
 2 2 1 362 2 2 1 362
 A. x 1 y z . B. x 1 y z .
 3 3 441 3 3 441
 2 2 2 2
 2 2 1 362 2 2 1 362
 C. x 1 y z . D. x 1 y z 
 3 3 21 3 3 21
 Lời giải
 Giả sử H x; y; z .
 2 1 
 Vì G là trọng tâm tam giác ABC nên G 1; ; .
 3 3 
       
 AH x; y; z 1 , BC 3; 2;0 , BH x; y 2;z , AC 3;0; 1 , AC, BC 2; 3; 6 .
 Vì H là trực tâm tam giác ABC nên
 36
   z 
 49
 AH.BC 0 3x 2y 0 
   18
 BH.AC 0 3x z 0 y .
    49
 AC, BC .AH 0 2x 3y 6z 6
 12
 x 
 49
 12 18 36 362
 H ; ; HG .
 49 49 49 21
 2 2
 2 2 1 362
 Khi đó mặt cầu tâm G và đi qua H có phương trình là x 1 y z .
 3 3 441
Câu 14: Trong không gian Oxyz cho A 2;0;0 ; B 0; 2;0 ; C 0;0; 2 . D là điểm khác O sao cho 
 DA, DB, DC đôi một vuông gó C. I a;b;c là tâm mặt cầu ngoại tứ diện ABCD . Tính 
 S a b c .
 A. 4 . B. 1. C. 2 . D. 3.
 Lời giải
    
 Gọi D x; y; z DA x 2; y; z ; DB x; y 2; z ; DC x; y; z 2 .
 Vì DA, DB, DC đôi một vuông góc nên:
   
 DA.DB 0 x x 2 y y 2 z2 0
   
 2 4
 DA.DC 0 x x 2 y z z 2 0 x y z .
   3
 2
 DB.DC 0 x y y 2 z z 2 0
 I a;b;c là tâm mặt cầu ngoại tiếp tứ diện ABCD nên:
 Page 11