Tài liệu ôn thi tốt nghiệp THPT - Chuyên đề 21: Ứng dụng tích phân tính diện tích hình phẳng và thể tích vật thể đơn giản

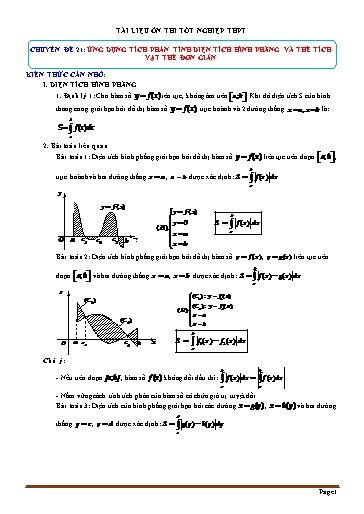
 TÀI LIỆU ÔN THI TỐT NGHIỆP THPT
 CHUYÊN ĐỀ 21: ỨNG DỤNG TÍCH PHÂN TÍNH DIỆN TÍCH HÌNH PHẲNG VÀ THỂ TÍCH 
 VẬT THỂ ĐƠN GIẢN
KIẾN THỨC CẦN NHỚ:
 I. DIỆN TÍCH HÌNH PHẲNG
 1. Định lý 1: Cho hàm số y f (x)liên tục, không âm trên a;b . Khi đó diện tích S của hình 
 thang cong giới hạn bởi đồ thị hàm số y f (x), trục hoành và 2 đường thẳng x a,x b là: 
 b
 S f (x)dx
 a
 2. Bài toán liên quan
 Bài toán 1: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y f (x) liên tục trên đoạn a;b , 
 b
 trục hoành và hai đường thẳng x a , x b được xác định: S f (x) dx
 a
 y
 y f (x)
 y f (x)
 b
 y 0 S f (x) dx
 (H) 
 x a a
 c 
 O a 1 c c3 b x
 2 x b
 Bài toán 2: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y f (x) , y g(x) liên tục trên 
 b
 đoạn a;b và hai đường thẳng x a , x b được xác định: S f (x) g(x) dx
 a
 y
 (C1 ) : y f1 (x)
 (C1 ) 
 (C ) : y f (x)
 (H ) 2 2
 x a
 (C )
 2 
 x b
 b
 a c x S f1(x ) f2(x ) dx
 O 1 c2 b 
 a
 Chú ý:
 b b
 - Nếu trên đoạn [a;b] , hàm số f (x) không đổi dấu thì: f (x) dx f (x)dx
 a a
 - Nắm vững cách tính tích phân của hàm số có chứa giá trị tuyệt đối
 Bài toán 3: Diện tích của hình phẳng giới hạn bởi các đường x g(y) , x h(y) và hai đường 
 d
 thẳng y c , y d được xác định: S g(y) h(y) dy
 c
 Page 1 Chọn D
 Phương trình hoành độ giao điểm của đường y x2 2x và đường y 0 là
 2 x 0
 x 2x 0 .
 x 2
 2 2 5 3
 2
 2 4 3 2 x 4 x 2 16 
 Thể tích là V x 2x dx x 4x 4x dx x 4. .
 0 0 5 3 0 15
Câu 1: Diện tích hình phẳng được gạch chéo trong hình bên bằng
 2 2
 A. 2x2 2x 4 dx . B. 2x2 2x 4 dx .
 1 1 
 2 2
 C. 2x2 2x 4 dx . D. 2x2 2x 4 dx .
 1 1 
 Lời giải
 Chọn A
 Dựa và hình vẽ ta có diện tích hình phẳng được gạch chéo trong hình bên là:
 2 2
 x2 2 x2 2x 2 dx 2x2 2x 4 dx.
 1 1 
Câu 2: Diện tích S của hình phẳng giới hạn bởi các đường y 2x 2 , y 1, x 0 và x 1 được tính 
 bởi công thức nào sau đây?
 1 1
 A. S 2x2 1 dx . B. S 2x2 1 dx .
 0 0
 1 1
 2
 C. S 2x2 1 dx . D. S 2x2 1 dx .
 0 0
 Lời giải
 Chọn D
 1 1
 Diện tích hình phẳng cần tìm là S 2x2 1 dx 2x2 1 dx do 2x2 1 0 x 0;1 .
 0 0
Câu 3: Diện tích hình phẳng giới hạn bởi hai đường y x2 4 và y 2x 4 bằng
 4 4 
 A. 36 . B. . C. . D. 36 .
 3 3
 Lời giải
 Chọn B
 Phương trình hoành độ giao điểm của hai đồ thị đã cho là:
 Page 3 2 2
 S 2x dx 2x dx .
 0 0
Câu 8: Gọi S là diện tích hình phẳng giới hạn bởi các đường y ex , y 0, x 0 , x 2 . Mệnh đề 
 nào dưới đây đúng?
 2 2 2 2
 A. S exdx B. S exdx C. S exdx D. S e2xdx
 0 0 0 0
 Lời giải
 Chọn A
 2
 Diện tích hình phẳng giới hạn bởi các đường y ex , y 0, x 0 , x 2 là: S exdx .
 0
Câu 9: Cho hàm số y f x liên tục trên ¡ . Gọi S là diện tích hình phẳng giới hạn bởi các đường 
 y f x , y 0, x 1 và x 5 .
 Mệnh đề nào sau đây đúng?
 1 5 1 5
 A. S f (x)dx f (x)dx . B. S f (x)dx f (x)dx .
 1 1 1 1
 1 5 1 5
 C. S f (x)dx f (x)dx . D. S f (x)dx f (x)dx .
 1 1 1 1
 Lời giải
 Chọn C
 1 5 1 5
 Ta có: S f (x) dx f x dx f x dx f x dx .
 1 1 1 1
Câu 10: Cho hàm số f x liên tục trên ¡ . Gọi S là diện tích hình phẳng giới hạn bởi các đường 
 y f x , y 0, x 1, x 2 . Mệnh đề nào dưới đây đúng?
 1 2 1 2
 A. S f x dx + f x dx . B. S f x dx f x dx .
 1 1 1 1
 Page 5 A. S b a B. S b a C. S b a D. S b a
 Lời giải
 Chọn A
 Ta có:
 2 0 2 0 2
 S f x dx f x dx f x dx f x dx f x dx a b .
 1 1 0 1 0
Câu 13: Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?
 2 2
 A. 2x 2 dx B. 2x 2 dx
 1 1
 2 2
 C. 2x2 2x 4 dx D. 2x2 2x 4 dx
 1 1
 Lời giải
 Chọn C
 Diện tích hình phẳng gạch chéo trong hình vẽ là:
 Page 7 1 3
 Do f x 0 với x  2;1 và f x 0 với x 1;3 nên S f x dx f x dx.
 2 1
Câu 16: Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong, giới 
 hạn bởi đồ thị hàm số y f x , trục Ox và hai đường thẳng x a, x b a b , xung quanh 
 trục Ox .
 b b b b
 A. V f x dx B. V f 2 x dx C. V f 2 x dx D. V f x dx
 a a a a
 Lời giải
 Chọn B
Câu 17: Cho hàm số y f x liên tục trên đoạn a;b . Gọi D là hình phẳng giới hạn bởi đồ thị hàm số 
 y f x , trục hoành và hai đường thẳng x a, x b a b . Thể tích của khối tròn xoay tạo 
 thành khi quay D quanh trục hoành được tính theo công thức:
 b b b b
 A. V 2 f x dx B. V f 2 x dx C. V 2 f 2 x dx D. V 2 f 2 x dx
 a a a a
 Lời giải
 Chọn B
Câu 18: Gọi D là hình phẳng giới hạn bởi các đường y e3x , y 0, x 0 và x 1. Thể tích của khối 
 tròn xoay tạo thành khi quay D quanh trục Ox bằng:
 1 1 1 1
 A. e3xdx . B. e6xdx . C. e6xdx . D. e3 xdx .
 0 0 0 0
 Lời giải
 Chọn C
 Ta có thể tích của khối tròn xoay tạo thành khi quay D quanh trục O x bằng:
 1 1
 2
 e3 x dx e6 xdx .
 0 0
 4x
Câu 19: Gọi D là hình phẳng giới hạn bởi các đường y e , y 0,x 0 và x 1 . Thể tích của khối 
 tròn xoay tạo thành khi quay D quanh trục O x bằng
 1 1 1 1
 A. e4xdx . B. e8xdx . C. e 4 x dx . D. e8 xdx .
 0 0 0 0
 Lời giải
 Chọn B
 Thể tích của khối tròn xoay tạo thành khi quay D quanh trục O x là:
 1 1
 2
 V e 4 x dx e8 x dx.
 0 0
 2x
Câu 20: Gọi D là hình phẳng giới hạn bởi các đường y e , y 0,x 0 và x 1 . Thể tích khối tròn 
 xoay tạo thành kho quay D quanh O x bằng
 1 1 1 1
 A. e4xdx . B. e2xdx. C. e2xdx . D. e4xdx.
 0 0 0 0
 Lời giải
 Page 9