Tài liệu ôn thi tốt nghiệp THPT - Chuyên đề 19: Xét tính đơn điệu dựa vào bảng biến thiên và đồ thị

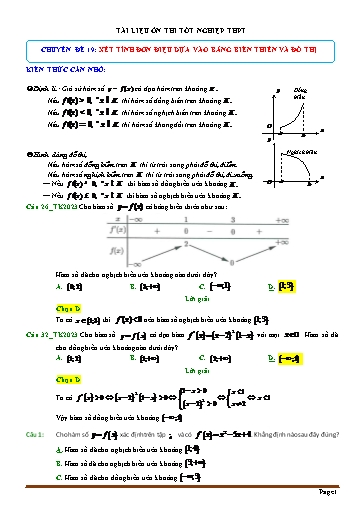
 TÀI LIỆU ÔN THI TỐT NGHIỆP THPT
 CHUYÊN ĐỀ 19: XÉT TÍNH ĐƠN ĐIỆU DỰA VÀO BẢNG BIẾN THIÊN VÀ ĐỒ THỊ
KIẾN THỨC CẦN NHỚ:
 Định lí : Giả sử hàm số y = f (x) có đạo hàm trên khoảng K . y Đồng 
 Nếu f ¢(x) > 0, " x Î K thì hàm số đồng biến trên khoảng K . biến
 Nếu f ¢(x) < 0, " x Î K thì hàm số nghịch biến trên khoảng K .
 Nếu f ¢(x) = 0, " x Î K thì hàm số không đổi trên khoảng K . O
 x
 a b
 y
 Hình dáng đồ thị Nghịch biến
 Nếu hàm số đồng biến trên K thì từ trái sang phải đồ thị đi lên.
 Nếu hàm số nghịch biến trên K thì từ trái sang phải đồ thị đi xuống. x
 — Nếu f ¢(x) ³ 0, " x Î K thì hàm số đồng biến trên khoảng K . O a b
 — Nếu f ¢(x) £ 0, " x Î K thì hàm số nghịch biến trên khoảng K .
Câu 26_TK2023 Cho hàm số y f (x) có bảng biến thiên như sau:
 Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
 A. 0;2 . B. 3; . C. ;1 . D. 1;3 .
 Lời giải
 Chọn D
 Ta có x 1;3 thì f '(x) 0 nên hàm số nghịch biến trên khoảng 1;3 .
 2
Câu 32_TK2023 Cho hàm số y f x có đạo hàm f x x 2 1 x với mọi x ¡ . Hàm số đã 
 cho đồng biến trên khoảng nào dưới đây?
 A. 1;2 . B. 1; . C. 2; . D. ;1 .
 Lời giải
 Chọn D
 1 x 0
 2 x 1
 Ta có f x 0 x 2 1 x 0 2 x 1.
 x 2 0 x 2
 Vậy hàm số đồng biến trên khoảng ;1 .
 2
Câu 1: Cho hàm số y f x xác định trên tập ¡ và có f x x 5x 4 . Khẳng định nào sau đây đúng?
 A. Hàm số đã cho nghịch biến trên khoảng 1;4 .
 B. Hàm số đã cho nghịch biến trên khoảng 3; .
 C. Hàm số đã cho đồng biến trên khoảng ;3 .
 Page 1
 Lời giải
 2
 Xét hàm số y f x có f x x x 1 x2 1 x x 1 x 1 .
 x 0
 2 
 f x 0 x x 1 x 1 0 x 1 .
 x 1
 Suy ra bảng xét dấu của hàm f x :
 Từ bảng xét dấu của hàm f x suy ra hàm số y f x nghịch biến trên khoảng 1;0 
 2
Câu 5: Cho hàm số y f x có đạo hàm f x x 1 x 2 x 4 . Hàm số y f x 1 đồng biến 
 trên khoảng nào dưới đây?
 A. 5;1 . B. 0; . C. ;0 . D. 0;1 .
 Lời giải
 x 1
 2 
 Ta có f x 0 x 1 x 2 x 4 0 x 2
 x 4
 x 1 1 x 0
 y f x 1 0 x 1 2 x 1
 x 1 4 x 5
 Bảng biến thiên
 Hàm số đồng biến trên khoảng ;0 .
 2
Câu 6: Cho hàm số y f x có đạo hàm f x 1 x 2 x x 4 . Hàm số y f x đồng biến trên 
 khoảng nào dưới đây?
 A. 4;2 . B. 0; . C. ;0 . D. 1; .
 Lời giải
 x 1
 Ta có 2 
 f x 0 1 x 2 x x 4 0 x 2
 x 4
 Bảng xét dấu đạo hàm
 Page 3
 Lời giải
 x 5
 Ta có 2 
 f x 0 x 2 x 5 x 1 0 x 1
 x 2
 Bảng xét dấu đạo hàm
 Hàm số đồng biến trên khoảng ; 5 ; 2; .
 2
Câu 11: Cho hàm số y f x có đạo hàm f x x 2 x 5 x 1 . Hàm số y f x nghịch biến 
 trên khoảng nào dưới đây?
 A. 4; 2 . B. ; 1 . C. ; 5 . D. 3;4 .
 Lời giải
 x 5
 Ta có 2 
 f x 0 x 2 x 5 x 1 0 x 1
 x 2
 Bảng xét dấu đạo hàm
 Hàm số nghịch biến trên khoảng 5;2 .
Câu 12: Cho hàm số y f (x) có bảng biến thiên như sau :
 Hàm số đã cho đồng biến trên khoảng nào dưới đây?
 A. 0; . B. ; 2 . C. 0;2 . D. 2;0 .
 Lời giải
 Chọn D
 Từ bảng biến thiên suy ra hàm số đã cho đồng biến trên 2;0 .
Câu 13: Hàm số nào dưới đây nghịch biến trên ¡ ?
 x 2
 A. y x3 x . B. y x4 x2 . C. y x3 x . D. y .
 x 1
 Lời giải
 Chọn A
 Hàm số y x3 x có y 3x2 1 0,x ¡ nên hàm số này nghịch biến trên ¡ .
Câu 14: Cho hàm số f x có bảng biến thiên như sau:
 Page 5
 Chọn C
 Dựa vào bảng biến thiên hàm số y f x đồng biến trên các khoảng ; 1 và 1;0 .
 Vậy hàm số đồng biến trên khoảng 1;0 .
Câu 18: Cho hàm số y x3 3x2 1. Khẳng định nào sau đây là đúng?
 A. Hàm số đồng biến trên khoảng 0;2 . B. Hàm số đồng biến trên khoảng ;0 .
 C. Hàm số đồng biến trên khoảng 2; . D. Hàm số nghịch biến trên khoảng 0;2 .
 Lời giải
 Chọn A
 2 x 0
 y 3x 6x . y 0 .
 x 2
 Bảng biến thiên:
 .
 Hàm số đồng biến trên khoảng 0;2 .
 2
Câu 19: Cho hàm số y f x có đạo hàm f x 2x 4 cosx , x ¡ . Mệnh đề nào dưới đây đúng?
 A. Hàm số nghịch biến trên khoảng ;0 . B. Hàm số nghịch biến trên khoảng 1; .
 C. Hàm số nghịch biến trên khoảng 1;1 . D. Hàm số đồng biến trên khoảng ; .
 Lời giải
 Chọn D
 Ta có Ta có f x 2x2 4 cos x 0, x ¡ Hàm số đồng biến trên khoảng ; .
Câu 20: Cho hàm số f x có đạo hàm là f x x 2 x 5 x 1 . Hàm số f x đồng biến trên khoảng 
 nào dưới đây?
 A. 2; . B. 2;0 . C. 0;1 . D. 6; 1 .
 Lời giải
 Chọn A
 x 5
 Cho f x 0 x 1 .
 x 2
 Ta có bảng xét dấu của f x như sau:
 Page 7
 Từ đó ta được y 0,x 1.
Câu 23: Cho hàm số f x có đồ thị như hình vẽ. Hàm số đã cho đồng biến trên khoảng nào trong các khoảng 
 sau đây?
 A. 0;1 . B. ;1 . C. 1;1 . D. 1;0 .
 Lời giải
 Chọn D
Câu 24: Cho hàm số f x có đồ thị như hình vẽ bên. Hàm số đã cho nghịch biến trên khoảng nào trong các 
 khoảng sau?
 A. 0;2 . B. 2;0 . C. 3; 1 . D. 2;3 .
 Lời giải
 Chọn D
Câu 25: Hình bên là đồ thị của hàm số y f x y. Hỏi hàm số y f x đồng biến trên khoảng nào dưới đây?
 y
 O 1 2 x
 A. 2; . B. 1;2 . C. 0;1 . D. 0;1 và 2; .
 Lời giải
 Chọn A
 Dựa vào đồ thị ta thấy f x 0,x 2 nên y f x đồng biến trên khoảng 2; .
Câu 26: Cho hàm số y f x xác định, liên tục trên ¡ và có đạo hàm f x . Biết rằng hàm số f x có đồ 
 thị như hình vẽ bên. Mệnh đề nào sau đây đúng?
 Page 9
 C. Hàm số nghịch biến trên khoảng 1; . D. Hàm số nghịch biến trên khoảng 0;1 .
 Lời giải
 Chọn D
 Dựa vào bảng biến thiên ta thấy f x 0 trên khoảng 0;1 hàm số nghịch biến trên 0;1 .
Câu 29: Cho hàm số y f x có bảng biến thiên như sau:
 Hàm số đã cho đồng biến trên khoảng nào dưới đây?
 A. ; 2 . B. 1; . C. 1;1 . D. ; 2 .
 Lời giải
 Chọn D
 Dựa vào bảng biến thiên ta thấy f ' x 0 trên khoảng ; 1 hàm số đồng biến trên 
 ; 1 nên cũng đồng biến trên ; 2 .
Câu 30: Cho hàm số y = f (x) có bảng biến thiên sau:
 x 3 2 1 
 y 0 0 
 2 
 y
 0
 Hàm số đã cho đồng biến trên khoảng nào dưới đây?
 3 
 A. 2; . B. 0; . C. ; 2 . D. ; .
 2 
 Lời giải
 Chọn C
 Dựa vào bảng biến thiên ta thấy f ' x 0 trên các khoảng ; 3 và 1; hàm số đồng 
 biến trên ; 3 và 1; hàm số đồng biến trên 0; .
Câu 31: Cho hàm số y f x có bảng biến thiên như hình vẽ:
 x 1 0 1 
 y 0 0 0 
 5 
 y
 3 3
 Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
 Page 11