Phiếu bài tập dạy thêm - Chuyên đề: Ứng dụng của định lí Thales trong tam giác - Toán 8 Kết nối tri thức

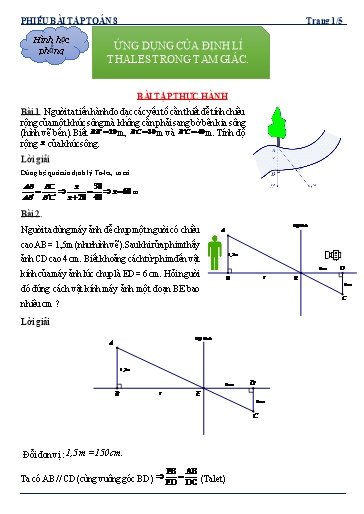
 PHIẾU BÀI TẬP TỐN 8 Trang 1/5
 Hình học 
 phẳng ỨNG DỤNG CỦA ĐỊNH LÍ 
 THALES TRONG TAM GIÁC.
 BÀI TẬP THỰC HÀNH
Bài 1. Người ta tiến hành đo đạc các yếu tố cần thiết để tính chiều 
rộng của một khúc sơng mà khơng cần phải sang bờ bên kia sơng 
(hình vẽ bên). Biết BB 20 m, BC 30 m và B C 40 m. Tính độ 
rộng x của khúc sơng. 
Lời giải
Dùng hệ quả của định lý Ta-let, ta cĩ
 AB BC x 30
 x 60 m.
 AB B C x 20 40
Bài 2.
 Vật kính
Người ta dùng máy ảnh để chụp một người cĩ chiều A
cao AB = 1,5 m (như hình vẽ). Sau khi rửa phim thấy 
ảnh CD cao 4 cm. Biết khoảng cách từ phim đến vật 1,5m
 6cm D
kính của máy ảnh lúc chụp là ED = 6 cm. Hỏi người 
 B ? E
đĩ đứng cách vật kính máy ảnh một đoạn BE bao 4cm
nhiêu cm ? C
Lời giải
 Vật kính
 A
 1,5m
 6cm D
 B ? E
 4cm
 C
 Đổi đơn vị : 1,5 m = 150 cm.
 EB AB
Ta cĩ AB // CD (cùng vuơng gĩc BD) (Talet)
 ED DC PHIẾU BÀI TẬP TỐN 8 Trang 3/5
Bài 5. Tính chiều cao AB của ngơi nhà. Biết cái cây cĩ 
chiều cao ED = 2m và khoảng cách AE = 4m, EC = 2,5m. 
Lời giải
Ta cĩ: ED//AB
 AB AC
 =
 ED EC
 AB 4 2,5
 2 2,5
 AB 6,5
 2 2,5
 6,5.2
 AB = = 5,2m
 2,5
Vậy ngơi nhà cao 5,2m
Bài 6.
Một cột đèn cao 10m chiếu sáng một cây xanh như hình bên dưới. Cây cách cột đèn 2m và cĩ 
bĩng trải dài dưới mặt đất là 4,8m. Tìm chiều cao của cây xanh đĩ (làm trịn đến mét).
 D B
 10m
 2m 4,8m
 C M
Lời giải
MC = MA+AC = 4,8+2 = 6,8 (m) 
 AB MA
 (Hệ quả của định lý Ta-let ) 
Xét DCM cĩ AB // CD nên : CD MC
 AB 4,8
 10 6,8
 AB 7 ( m )
Bài 7. PHIẾU BÀI TẬP TỐN 8 Trang 5/5
Bài 9: Bĩng của một tháp trên mặt đất cĩ độ dài 
BC = 63 mét. Cùng thời điểm đĩ, một cây cột DE 
cao 2 mét cắm vuơng gĩc với mặt đất cĩ bĩng dài 3 
mét. Tính chiều cao của tháp? 
Lời giải
*DE / /AB (cùng vuông góc BC)
 DE CE
 ( Hệ quả Talet)
 AB CB
 2 3
 AB 63
 AB 42m
Vậy chiều cao của Tháp là 42m A
 2m
 E
Bài 10: Giữa hai điểm B và C cĩ một cái ao. Để đo khoảng cách BC người ta D 5m
đo được các đoạn thẳng AD = 2m,BD = 10m và DE = 5m. Biết DE // BC, tính 10m
khoảng cách giữa hai điểm B và C.
Lời giải B C
Xét tam giác ABC cĩ DE // BC
 (HQ của đl Ta-lét)
⇒ = 
⇒ = 30 . 
Vậy khoảng cách giữa hai điểm B và C là 30m
Bài 11: Để đo khoảng cách giữa hai điểm A và B (khơng 
thể đo trực tiếp). Người ta xác định các điểm C, D, E như 
hình vẽ. Sau đĩ đo được khoảng cách giữa A và C là AC = 
6m, khoảng cách giữa C và E là EC = 2m; khoảng cách giữa 
E và D là DE = 3m. Tính khoảng cách giữa hai điểm A và 
B.
Lời giải
Ta cĩ: AB // ED
 ED CE
=> =
 AB AC
 3 2
=> =
 AB 6
 6.3
=> AB = 9m
 2
Vậy chiều rộng AB của khúc sơng khoảng 9m