Phiếu bài tập dạy thêm - Chuyên đề: Tứ giác - Toán 8 Kết nối tri thức

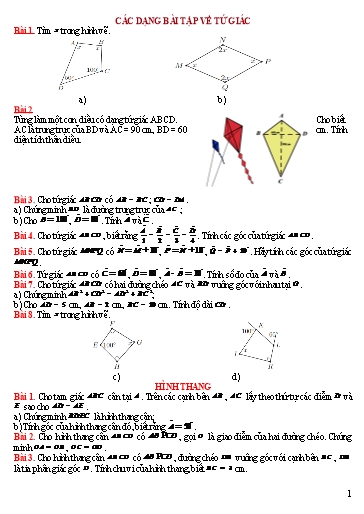
 CÁC DẠNG BÀI TẬP VỀ TỨ GIÁC
Bài 1. Tìm x trong hình vẽ.
 a) b) 
Bài 2
Tùng làm một con diều có dạng tứ giác ABCD. A Cho biết 
AC là trung trực của BD và AC = 90 cm, BD = 60 cm. Tính 
 B 60cm D
diện tích thân diều.
 90cm
 C
Bài 3. Cho tứ giác ABCD có AB = BC ; CD = DA .
a) Chứng minh BD là đường trung trực của AC ;
b) Cho Bˆ = 100° , Dˆ = 80° . Tính Aˆ và Cˆ .
 Aˆ Bˆ Cˆ Dˆ
Bài 4. Cho tứ giác ABCD , biết rằng = = = . Tính các góc của tứ giác ABCD .
 1 2 3 4
Bài 5. Cho tứ giác MNPQ có Nˆ = Mˆ + 10° , Pˆ = Nˆ + 10° , Qˆ = Pˆ + 10° . Hãy tính các góc của tứ giác 
MNPQ .
Bài 6. Tứ giác ABCD có Cˆ = 60° , Dˆ = 80° , Aˆ - Bˆ = 10° . Tính số đo của Aˆ và Bˆ .
Bài 7. Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau tại O .
a) Chứng minh AB 2 + CD 2 = AD 2 + BC 2 ;
b) Cho AD = 5 cm, AB = 2 cm, BC = 10 cm. Tính độ dài CD . 
Bài 8. Tìm x trong hình vẽ.
 c) d) 
 HÌNH THANG
Bài 1. Cho tam giác ABC cân tại A . Trên các cạnh bên AB , AC lấy theo thứ tự các điểm D và 
E sao cho AD = AE .
a) Chứng minh BDEC là hình thang cân;
b) Tính góc của hình thang cân đó, biết rằng Aˆ = 50° .
Bài 2. Cho hình thang cân ABCD có AB PCD , gọi O là giao điểm của hai đường chéo. Chứng 
minh OA = OB , OC = OD .
Bài 3. Cho hình thang cân ABCD có AB PCD , đường chéo DB vuông góc với cạnh bên BC , DB 
là tia phân giác góc D . Tính chu vi của hình thang, biết BC = 3 cm.
 1 b) Ba điểm M ,N,I thẳng hàng;
c) Ba đường thẳng A C,MN ,PQ đồng quy.
Bài 8. Cho hình bình hành A BCD . Gọi K , I lần lượt là trung điểm các cạnh A B và CD . Chứng 
minh:
 · ·
a) A I = CK và IAC = KCA ; b) A I PCK .
Bài 9. Cho hình bình hành A BCD , gọi O là giao điểm của hai đường chéo. Trên A B lấy điểm K , 
trên CD lấy điểm I sao cho A K = CI . Chứng minh rằng ba điểm K ,O,I thẳng hàng và các đường 
thẳng AC,BD,KI đồng quy.
Bài 10. Cho hình bình hành A BCD . Gọi O là giao điểm hai đường thẳng A C và BD . Qua điểm 
O , vẽ đường thẳng a cắt hai đường thẳng A D,BC lần lượt tại E,F . Qua O vẽ đường thẳng b cắt 
hai cạnh AB,CD lần lượt tại K ,H . Chứng minh tứ giác EK FH là hình bình hành.
 HÌNH CHỮ NHẬT
Bài 1. Cho tam giác ABC , đường cao AH . Gọi I là trung điểm của AC . Lấy D là điểm đối xứng 
với H qua I . Chứng minh tứ giác AHCD là hình chữ nhật.
Bài 2. Cho tam giác ABC vuông tại A , đường cao AH . Gọi I , K theo thứ tự là trung điểm của 
AB , AC . Chứng minh: I·HK 90 ;
Bài 3. Tìm độ dài CD trong hình vẽ bên, biết AB 9 cm, AD 4 cm, BC 5 cm.
Bài 4. Tìm độ dài CD trong hình vẽ bên, biết AB 7 cm, AD 8 cm, BC 10 cm.
Bài 5. Cho tam giác ABC vuông cân tại C . Trên các cạnh AC , BC lấy lần lượt các điểm P , Q 
sao cho AP CQ . Từ điểm P vẽ PM song song với BC ( M AB ). Chứng minh tứ giác PCQM Ià 
hình chữ nhật.
Bài 6. Cho tam giác ABC có đường cao AI . Từ A kẻ tia Ax vuông góc với AC , từ B kẻ tia By 
song song với AC . Gọi M là giao điểm của tia Ax và tia By . Nối M với trung điểm P của AB , 
đường MP cắt AC tại Q và BQ cắt AI tại H .
a) Tứ giác AMBQ là hình gì? b) Chứng minh tam giác PIQ cân. 
 HÌNH THOI
Bài 1. Cho góc xOy và tia phân giác Ot. Từ điểm M thuộc Oz kẻ MA // Oy và MB // Ox ( với 
A Ox; B Oy ). Chứng minh tứ giác OAMB là hình thoi.
Bài 2. Cho hình bình hành ABCD có 2 đường cao AH = AK . Chứng minh ABCD là hình thoi.
Bài 3. Cho hình thoi ABCD có Bˆ 60 . Kẻ AE  DC , AF  BC . Chứng minh
a) AE AF ; b) Tam giác AEF đều.
Bài 4. 
Hai đường chéo của hình thoi có độ dài 16cm và 12cm. Tính :
a/ Diện tích hình thoi b/ Cạnh hình thoi c/ Độ dài đường cao hình thoi.
Bài 5. Cho tam giác ABC , phân giác AD . Qua D kẻ đường thẳng song song với AC cắt AB tại E
, qua D kẻ đường thẳng song song với AB cắt AC tại F . Chứng minh EF là phân giác của ·AED.
Bài 6. 
a) Cạnh của một hình thoi bằng 25 , 
một đường chéo bằng 14. Tính độ dài đường chéo còn lại.
b) Cho hình thoi DEFG như hình vẽ bên. Tính x .
Bài 7. Cho hình bình hành ABCD có AC vuông góc với AD . Gọi E , F theo thứ tự là trung điểm 
của các cạnh AB , CD . Chứng minh tứ giác AECF là hình thoi.
Bài 8. Cho hình thoi ABCD tâm O . Độ dài AC 8 cm, BD 10 cm. Tính độ dài cạnh hình thoi. 
Bài 9. Cho hình thoi ABCD , gọi O là giao điểm của hai đường chéo. Trên cạnh AB , BC , CD , 
DA lấy theo thứ tự các điểm M , N , P , Q sao cho AM CN CP AQ . Chứng minh:
 3 Bài 6. Cho tam giác ABC vuông tại A , đường trung tuyến AM . Gọi H là điểm đối xứng với M qua AB , E là 
giao điểm của MH và AB . Gọi K là điểm đối xứng với M qua AC , F là giao điểm của MK và AC .
a) Các tứ giác AEMF , AMBH , AMCK là hình gì? Vì sao?
b) Chứng minh rằng H đối xứng với K qua A .
c) Tam giác vuông ABC cần thêm điều kiện gì thì tứ giác AEMF là hình vuông?
Bài 7. Cho hình bình hành ABCD có BC 2AB , Aˆ 60 . Gọi E , F theo thứ tự là trung điểm của BC , AD . 
Vẽ I đối xứng với A qua B .
a) Tứ giác ABEF là hình gì? Vì sao? b) Chứng minh tứ giác AIEF là hình thang cân.
c) Chứng minh BICD là hình chữ nhật. d) Tính góc ·AED.
Bài 8. Cho hình thang cân ABCD ( AB PCD, AB CD) , các đường cao AH , BK .
a) Tứ giác ABKH là hình gì? Vì sao?
b) Chứng minh DH CK .
c) Gọi E là điểm đối xứng với D qua H . Các điểm D và E đối xứng với nhau qua đường nào?
d) Tứ giác ABCE là hình gì?
Bài 9. Cho tam giác ABC vuông tại B . Gọi E, F lần lượt là trung điểm của AC , BC . Kẻ Ex song song với 
 BC cắt AB tại M .
a) Chứng minh tứ giác BMEF là hình chữ nhật.
b) Gọi K đối xứng với B qua E . Tứ giác BAKC là hình gì? Vì sao?
c) Gọi G đối xứng với E qua F . Tứ giác BGCE là hình gì? Vì sao?
d) Tam giác ABC cần thêm điều kiện gì để tứ giác BGCE là hình vuông?
Bài 10. Cho tam giác ABC vuông tại A có AB AC . Gọi M là trung điểm của BC , kẻ MD vuông góc với 
 AB tại D , ME vuông góc với AC tại E .
a) Chứng minh AM DE . b) Chứng minh tứ giác DMCE là hình bình hành.
c) Gọi AH là đường cao của tam giác ABC ( H BC ). Chứng minh tứ giác DHME là hình thang cân và A đối 
xứng với H qua DE .
 1
Bài 11. Cho hình thang vuông ABCD có Aˆ Dˆ 90 và AB AD CD , kẻ BH vuông góc với CD .
 2
a) Chứng minh rằng tứ giác ABHD là hình vuông.
b) Gọi M là trung điểm của BH . Chứng minh A đối xứng với C qua M .
c) Kẻ DI vuông góc với AC . AH cắt DI , DM tại P và Q . Chứng minh tứ giác DPBQ là hình thoi.
Bài 12. Cho hình vuông ABCD . E là điểm trên cạnh DC , F là điểm trên tia đối của tia BC sao cho BF DE .
a) Chứng minh tam giác AEF vuông cân.
b) Gọi I là trung điểm của EF . Chứng minh I thuộc BD .
c) Lấy điểm K đối xứng với A qua I . Chứng minh tứ giác AEKF là hình vuông.
Bài 13. Cho tam giác ABC vuông tại A , đường trung tuyến AM . Gọi D là trung điểm của AB , E là điểm đối 
xứng của M qua D .
a) Chứng minh E đối xứng với M qua đường thẳng AB . b) Các tứ giác AEMC , AEBM là hình gì? Vì sao?
c) Tam giác vuông ABC cần thêm điều kiện gì thì tứ giác AEBM là hình vuông?
Bài 14. Cho hình bình hành MNPQ có MN 2MQ và Mˆ 120 . Gọi I , K lần lượt là trung điểm của MN , PQ 
và A là điểm đối xứng của Q qua M .
a) Tứ giác MIKQ là hình gì? Vì sao? b) Chứng minh tam giác AMI đều.
c) Chứng minh tứ giác AMPN là hình chữ nhật.
Bài 15. Cho tứ giác ABCD , E là trung điểm của cạnh AB . Qua E kẻ đường thẳng song song với AC cắt BC ở 
 F . Qua F kẻ đường thẳng song song với BD cắt CD ở G . Qua G kẻ đường thẳng song song với AC cắt AD 
ở H .
a) Chứng minh tứ giác EFGH là hình bình hành.
b) Tứ giác ABCD cần thêm điều kiện gì để tứ giác EFGH là hình chữ nhật.
Bài 16. Cho tam giác ABC vuông ở A . Gọi E , G , F lần lượt là trung điểm của AB , BC , AC . Từ E kẻ 
đường thẳng song song với BF , đường thẳng này cắt GF tại I .
a) Tứ giác AEGF là hình gì? Vì sao? b) Chứng minh tứ giác BEIF là hình bình hành.
c) Chứng minh tứ giác AGCI là hình thoi. d) Tìm điều kiện của tam giác ABC để tứ giác AGCI là hình vuông.
 5