Phiếu bài tập dạy thêm - Chuyên đề: Tính chất đường phân giác của tam giác - Toán 8 Kết nối tri thức

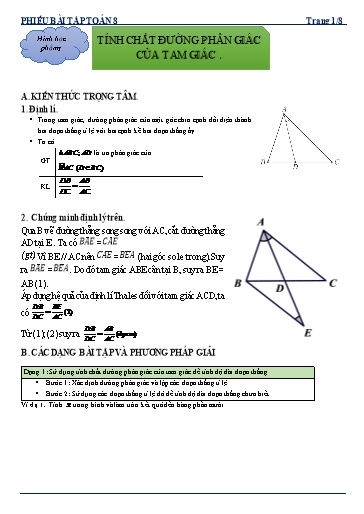
 PHIẾU BÀI TẬP TOÁN 8 Trang 1/8
 Hình học TÍNH CHẤT ĐƯỜNG PHÂN GIÁC 
 phẳng
 CỦA TAM GIÁC .
A. KIẾN THỨC TRỌNG TÂM.
1. Định lí.
 ▪ Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành 
 hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.
 ▪ Ta có 
 ABC; AD là tia phân giác của 
 GT
 B· AC (D BC)
 DB AB
 KL .
 DC AC
2. Chứng minh định lý trên. 
 A
Qua B vẽ đường thẳng song song với AC, cắt đường thẳng 
AD tại E . Ta có = 
(gt). Vì BE // AC nên = (hai góc so le trong). Suy 
ra = . Do đó tam giác ABE cân tại B, suy ra BE = 
AB (1).
 B D C
Áp dụng hệ quả của định lí Thales đối với tam giác ACD, ta 
 DB BE
có (2) 
 DC AC
 DB AB
Từ (1); (2) suy ra (dpcm)
 DC AC E
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
 Dạng 1: Sử dụng tính chất đường phân giác của tam giác để tính độ dài đoạn thẳng
 ▪ Bước 1: Xác định đường phân giác và lập các đoạn thẳng tỉ lệ.
 ▪ Bước 2: Sử dụng các đoạn thẳng tỉ lệ đó để tính độ dài đoạn thẳng chưa biết.
Ví dụ 1. Tính x trong hình và làm tròn kết quả đến hàng phần mười. PHIẾU BÀI TẬP TOÁN 8 Trang 3/8
b) Tính MN theo a , b . 
 BN a AB a b AN b BN a
Theo (2) có .
 AN b AN b AB a b AB a b
 BN MN BN a ab
Do MN P AC nên MN  AC b .
 BA AC BA a b a b
Ví dụ 3. Cho tam giác ABC có AB 12 cm, AC 20 cm, BC 28 cm. Đường phân giác góc A cắt BC 
tại D . Qua D kẻ DE//AB ( E AC ).
a) Tính độ dài các đoạn thẳng BD , DC và DE . ĐS: DB 10,5 ; DC 17,5 ; DE 7,5 .
b) Cho biết diện tích tam giác ABC là S . Tính diện tích các tam giác ABD , ADE , DCE theo S . 
 3 15 25
 ĐS: S S , S S , S S .
 V ABD 8 V ADE 64 VDCE 64
Lời giải
a) Theo tính chất đường phân giác trong góc A ta có
 DB AB DB 3 3
 DB DC ; (1)
 DC AC DC 5 5
Mặt khác DB DC BC 28. (2)
Từ (1) và (2) ta tính được DB 10,5 cm và DC 17,5 cm.
 DE DC DC 17,5
Vì DE P AB nên ta có DE  AB 12 7,5 cm.
 AB BC BC 28
b) Gọi AH là đường cao kẻ từ A của VABC . Ta có 
 1
 S  AH  BC ; 
 V ABC 2
 1
 S  AH  BD và 
 V ABD 2
 1
 S  AH CD .
 V ADC 2
 BD 3 CD 5
Suy ra S  S S và S  S  S .
 V ABD BC 8 V ADC BC 8
Chứng minh tương tự bằng cách trong VADC ta kẻ đường cao DF ta được 
 1
 S  DF  AC ; 
 V ADC 2
 1
 S  DF  AE và 
 V ADE 2
 1
 S  DF  EC .
 VDCE 2 PHIẾU BÀI TẬP TOÁN 8 Trang 5/8
Bài 2. Cho tam giác ABC , trung tuyến AM . Phân giác của ·AMB cắt AB ở D , phân giác của ·AMC cắt AC 
ở E .
a) Chứng minh DE song song với BC . 
b) Gọi I là giao điểm của DE và AM . Chứng minh I là trung điểm của DE .
Lời giải
a) Theo tính chất đường phân giác ta có
 DA MA EA MA
 và .
 DB MB EC MC
 DA EA
Mặt khác MB MC nên . Theo định lý Ta-lét đảo ta được 
 DB EC
 DE//BC .
 AD AE
b) Theo câu a) ta có DE P BC nên .
 AB AC
Xét định lý Ta-lét cho VABM và VACM ta có 
 AD DI AE IE
 và .
 AB BM AC CM
 DI IE
Từ đó, suy ra mà MB CM nên DI IE hay I là trung điểm của DE .
 BM CM
Bài 3. Cho tam giác ABC vuông tại A và AB 12 cm, AC 16 cm. Đường phân giác góc A cắt BC tại 
 D .
a) Tính BC , BD và CD . ĐS: BC 20 cm; BD 8, 6 cm; DC 11,4 cm.
b) Vẽ đường cao AH . Tính AH , HD và AD . ĐS: AH 9, 6 cm, HD 1, 4 cm, AD 9, 7 cm.
Lời giải
a) Áp dụng định lý Py-ta-go ta có
 BC AB2 AC 2 20 cm.
Theo tính chất đường phân giác trong của góc A ta có
 DB AB 3 3
 DB DC .
 DC AC 4 4
Mặt khác ta lại có
 3
 BD DC BC 20 DC DC 20 DC 11,4 cm.
 4
Do đó BD BC DC 20 11, 4 8, 6 cm. 
 1
b) Ta có S  AB  AC 96 cm.
 ABC 2 PHIẾU BÀI TẬP TOÁN 8 Trang 7/8
Lời giải
Hình a: Ta có BD 25 x .
Theo tính chất đường phân giác trong ta có 
 DB AB 25 x 20 75
 x 10,7 .
 DC AC x 15 7
Hình b: Ta có LJ 28 x .
Theo tính chất phân giác trong ta có 
 LK IK x 20 35
 x 17,5 .
 LJ IJ 28 x 12 2
Bài 6. Cho tam giác ABC , trung tuyến AM . Tia phân giác góc AMB cắt AB tại D , tia phân giác góc AMC 
cắt cạnh AC tại E . Chứng minh DE P BC .
Lời giải
Theo tính chất đường phân giác ta có
 DA MA EA MA
 và .
 DB MB EC MC
 DA EA
Mặt khác MB MC nên .
 DB EC
Theo định lý Ta-lét đảo ta được DE P BC .
Bài 7. Cho tam giác ABC có AB 15 cm, AC 20 cm, BC 25 cm. Đường phân giác góc A cắt BC tại 
 D . 
a) Tính độ dài các đoạn thẳng BD , DC . ĐS: DB 10,7 cm; DC 14,3 cm.
 107
b) Tính tỉ số diện tích hai tam giác ABD và ACD . ĐS: .
 143
Lời giải
a) Áp dụng tính chất đường phân giác trong góc A . Ta có
 DB AB DB 3 3
 DB DC ; (1)
 DC AC DC 4 4
Mặt khác DB DC BC 25. (2)
Từ (1) và (2) ta có tính được DB 10,7 cm và DC 14,3 cm.