Phiếu bài tập dạy thêm - Chuyên đề: Bài tập tổng hợp tam giác đồng dạng, hình đồng dạng - Toán 8 Kết nối tri thức

 PHIẾU BÀI TẬP TOÁN 8 Trang 1/14
 HÌNH BÀI TẬP TỔNG HỢP CHƯƠNG 
 HỌC TAM GIÁC ĐỒNG DẠNG & 
 PHẲNG
 HÌNH ĐỒNG DẠNG .
 BÀI TẬP THỰC HÀNH.
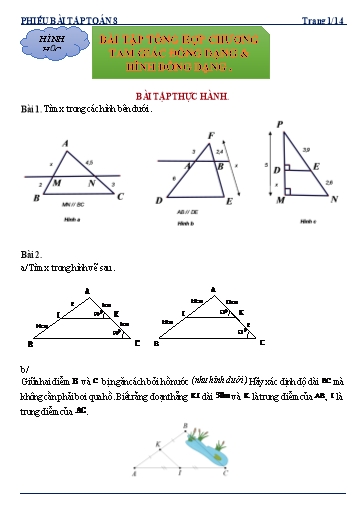
Bài 1. Tìm x trong các hình bên dưới .
 P
 F
 A
 3 2,4 3,9
 x 4,5 5
 A B x D E
 6
 2 M N 3 x 2,6
 B C N
 MN // BC D E M
 AB // DE
 Hình a
 Hình b Hình c
Bài 2.
a/ Tìm x trong hình vẽ sau .
 A A
 15cm
 x 8cm 11cm
 0
 I 500 K I 53 K
 15cm
 10cm 8cm x
 500 530
 B C B C
b/ 
Giữa hai điểm B và C bị ngăn cách bởi hồ nước (như hình dưới). Hãy xác định độ dài BC mà 
không cần phải bơi qua hồ. Biết rằng đoạn thẳng KI dài 30m và K là trung điểm của AB, I là 
trung điểm của AC. PHIẾU BÀI TẬP TOÁN 8 Trang 3/14
Bài 5. Một ngôi nhà có thiết kế mái như hình bên và có các số đo A
như sau : AD = 1,5m; DE = 2,5m; BF = GC = 1m; FG = 5,5 m. 1,5m
 D 2,5m E
Tính chiều dài của mái nhà bên, biết DE // BC. 
Lời giải 5,5m
 B C
Ta có BC = BF + FG + GC = 1 + 5,5 + 1 = 7,5 m F G
Vì DE // BC nên áp dụng định lý Thales ta có :
 DE AD
 BC AB
 2,5 1,5
 7,5 AB
 1 1,5
 3 AB
 AB 1,5.3 4,5m
Vậy chiều dài của mái nhà bên là 4,5m
Bài 6. Cho tam giác ABC nhọn, các đường cao AD , BE , CF cắt nhau tại H . Chứng minh
a) VHBF ~VHCE . b) HB  HE HF  HC HA HD .
c) EH là tia phân giác của góc DEF .
Lời giải
a) VHBF ~VHCE (g.g).
b) Từ kết quả câu a) ta có HB  HE HF  HC .
Làm tương tự ta thu được HF  HC HA HD . Suy ra 
 HB  HE HF  HC HA HD .
c) Từ câu b), chứng minh được
VEHF ~VCHB (c.g.c) và V DHE ~V BHA (c.g.c), do đó
 H· EF H· CB và H· ED H· AB . 
Ta có H· AB H· CB (cùng phụ ·ABC ).
Do đó H· ED H· EF 
 EH là tia phân giác của góc DEF . PHIẾU BÀI TẬP TOÁN 8 Trang 5/14
Lời giải
a) Xét VBMO , ta có B· MO 180 ·ABC M· OB . 
Ta cũng có C· ON 180 M· ON M· OB 120 M· OB
 B· MO C· ON VBMO ~VCON (g.g). 
 OM BM BM
b) Từ kết quả câu a), ta có vì OB OC .
 ON CO BO
c) Từ kết quả câu b), Bˆ M· ON 60 . 
Do đó VBMO ~VOMN (c.g.c). 
Vậy MO là tia phân giác của BMO .
Bài 10. Cho tam giác ABC vuông tại A có AB 6 cm, AC 8 cm. Kẻ đường cao AH .
a) Chứng minh AH  BC AB  AC 
b) Gọi M , N lần lượt là hình chiếu của H trên AB , AC . Chứng minh VAMN ~VACB .
c) Tính diện tích tứ giác BMNC . ĐS{18,4704 cm 2 }
Lời giải
a) Ta có VABH ~VCAB (g.g) 
 AH AB
 AH  BC AB  AC 
 CB CA
b) Ta giả thiết ta có ·ABC H· MA H· NA 90
 AMHN là hình chữ nhật.
Do ANHM là hình chữ nhật nên ta có ·ANM ·AHM . 
Mặt khác ·AHM ·ABC (cùng phụ H· AB ) 
 VAMN ~VACB (g.g).
 1
c) Ta có S AB  AC 4,8 (cm 2 ). Từ kết quả câu c), ta tính được S 5,5296 cm 2 
 V ABC 2 AMN
 2
 SBMNC 18,4704 cm .
Bài 11. Cho hình chữ nhật ABCD có AD 6 cm, AB 8 cm. Gọi O là giao điểm của AC và 
 BD . Qua D kẻ đường thẳng d vuông góc với BD , d cắt tia BC tại E . Chứng minh
a) VBDE ~VDCE .
b) Kẻ CH  DE tại H . Chứng minh DC 2 CH  DB .
c) Gọi K là giao điểm của OC và HC . Chứng minh K là trung điểm của HC . PHIẾU BÀI TẬP TOÁN 8 Trang 7/14
Lời giải
a) Ta có VANB ~VAPC (g.g) 
 AN AB
 AN  AC AP  AB .
 AP AC
b) Từ kết quả câu a) ta có VANP ~VABC (c.g.c)
c) Ta có EP P NC , FN PBP nên theo định lý Ta-lét ta có 
 HE HP HF HN HE HF
 , . Do đó EF PBC .
 HN HC HP HB HB HC
Bài 14. Cho tam giác ABC vuông tại A (AB AC) và trung tuyến AD . Qua D kẻ đường thẳng 
vuông góc với AD cắt AC và AB lần lượt tại E và F . 
a) Chứng minh VABC ~VAEF .
b) Chứng minh BC 2 4DE  DF .
Lời giải
a) Ta có VDAC cân tại D nên 
 ·ACB D· AC 90 D· AF ·AFE 
 VABC ~VAEF (g.g).
b) Theo câu a) ta có ·AFE ~ ·ACB VDEC ~VDBF (g.g) 
 BC 2 4DE  DF .
Bài 15 Cho tam giác ABC vuông tại A (AB > AC). Gọi I là 
trung điểm của AB. Kẻ IN vuông góc với BC tại N (N thuộc BC).
a/ Chứng minh : ∆ACB đồng dạng với ∆NIB. Từ đó suy ra BA.BI = BC.BN
b/ Giả sử AC = 6cm; BC = 10cm. Tính BN. 
c/ Chứng minh IAN = ICN 
d/ Chứng minh : AC2 = NC2 ― NB2
Lời giải B
a/ Chứng minh : 
 ∆ACB đồng dạng với ∆NIB (g,g) N
 I
Từ tỉ số suy ra BA.BI = CB.BN H
b/ Tính được BN = 3,2cm 
 A C
 BI BC
c/ Từ tỉ số Chứng minh ∆BIC đồng dạng với ∆BNA
 BN BA
Từ đó suy ra IAN = ICN
d/ Kẻ AH BC tại H. Chứng minh được AC2 = CH.CB
Chứng minh N là trung điểm HB NB = NH PHIẾU BÀI TẬP TOÁN 8 Trang 9/14
 MỘT SỐ ĐỀ THỰC HÀNH CHƯƠNG
 TAM GIÁC ĐỒNG DẠNG & HÌNH ĐỒNG DẠNG
 ĐỀ THỰC HÀNH SỐ 01
A. PHẦN TRẮC NGHIỆM
Câu 1. Cho tam giác ABC có M , N lần lượt nằm trên hai cạnh AB , AC sao cho MN PBC . Biết 
 AM 16 cm, AN 20 cm, NC 15 cm. Khi đó độ dài AB bằng
A. 28 cm. B. 26 cm. C. 24 cm. D. 22 cm.
Câu 2. Cho tam giác ABC có AB 3 cm, AC 4 cm, BC 5 cm và tam giác DEF có DE 6 
cm, DF 8 cm, EF 10 cm. Cách viết nào sau đây đúng quy ước về đỉnh:
A. VABC ∽ VFED . B. VABC ∽ VDEF . C. VCAB ∽ VDEF . D. VBCA∽ VEDF .
Câu 3. Cho tam giác ABC đồng dạng với tam giác MNP theo tỉ số đồng dạng 3 . Gọi H , K lần 
 BH
lượt là trung điểm của AC , MP . Tỉ số bằng
 NK
 1 1
A. . B. . C. 3 . D. 9 .
 3 9
 AB
Câu 4. Cho tam giác ABC đồng dạng với tam giác PQR có 4, S 32 cm 2 . Diện tích 
 PQ V ABC
tam giác PQR bằng
A. 128 cm 2 . B. 64 cm 2 . C. 16 cm 2 . D. 2 cm 2 .
Câu 5. Cho hình vẽ bên. Điền nội dung thích hợp vào chỗ chấm 
()
 DB 
a) 
 DC 
 DB 
b) Nếu thì DE P AB .
 DC 
c) Nếu DE P AB thì EA  .
II. PHẦN TỰ LUẬN
Bài 1. Người ta tiến hành đo đạc các yếu tố cần thiết để tính 
chiều rộng của một khúc sông mà không cần phải sang bờ bên 
kia sông (hình vẽ bên). Biết BB 20 m, BC 30 m và 
 B C 40 m. Tính độ rộng x của khúc sông.
Bài 2. Cho tam giác ABC nhọn có AB AC và các đường cao 
 AD , BE , CF cắt nhau tại H .
a) Chứng minh HE  HB HF  HC .
b) Chứng minh VEHF ~VCHB . PHIẾU BÀI TẬP TOÁN 8 Trang 11/14
 ĐÁP ÁN ĐỀ SỐ 01
A. PHẦN TRẮC NGHIỆM
Câu 1. Cho tam giác ABC có M , N lần lượt nằm trên hai cạnh AB , AC sao cho MN PBC . Biết 
 AM 16 cm, AN 20 cm, NC 15 cm. Khi đó độ dài AB bằng
A. 28 cm. B. 26 cm. C. 24 cm. D. 22 cm.
Lời giải
 AM AN
Theo định lý Ta-lét ta có 
 MB NC
 AM  NC
 MB 12 cm 
 AN
 AB 16 12 28 (cm).
Câu 2. Cho tam giác ABC có AB 3 cm, AC 4 cm, 
 BC 5 cm và tam giác DEF có DE 6 cm, DF 8 cm, EF 10 cm. Cách viết nào sau đây 
đúng quy ước về đỉnh:
A. VABC ∽ VFED .B. VABC ∽ VDEF . C. VCAB ∽ VDEF . D. VBCA∽ VEDF .
Lời giải
 AB AC BC
Ta có 2 VABC ∽ VDEF (c.c.c).
 DE DF EF
Câu 3. Cho tam giác ABC đồng dạng với tam giác MNP theo tỉ số đồng dạng 3 . Gọi H , K lần 
 BH
lượt là trung điểm của AC , MP . Tỉ số bằng
 NK
 1 1
A. . B. .C. 3 . D. 9 .
 3 9
Lời giải
 BH
Ta có 3 . 
 NK
 AB
Câu 4. Cho tam giác ABC đồng dạng với tam giác PQR có 4, S 32 cm 2 . Diện tích 
 PQ V ABC
tam giác PQR bằng
A. 128 cm 2 . B. 64 cm 2 . C. 16 cm 2 .D. 2 cm 2 .
Lời giải
 2
 SV ABC AB 32 2
Ta có 2 16 SVPQR 2 cm .
 SVPQR PQ 16