Ôn tập Toán 9 - Chuyên đề 3: Các tỉ số lượng giác

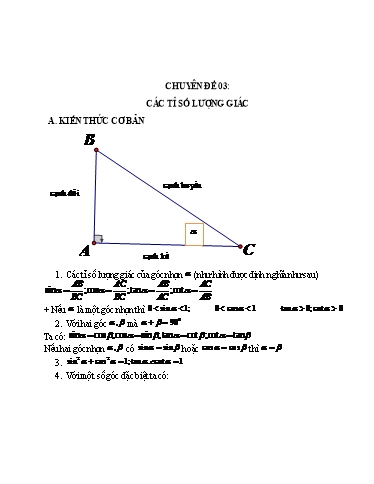
 CHUYÊN ĐỀ 03:
 CÁC TỈ SỐ LƯỢNG GIÁC
 A. KIẾN THỨC CƠ BẢN
 B
 cạnh huyền
 cạnh đối
 A cạnh kề C
 1. Các tỉ số lượng giác của góc nhọn (như hình được định nghĩa như sau)
 AB AC AB AC
 sin ;cos ;tan ;cot 
 BC BC AC AB
+ Nếu là một góc nhọn thì 0 sin 1; 0 cos 1 tan 0;cot 0 
 2. Với hai góc , mà  900 
Ta có: sin cos ;cos sin ;tan cot ;cot tan  
Nếu hai góc nhọn , có sin sin  hoặc cos cos  thì  
 3. sin2 cos2 1;tan .ccot 1 
 4. Với một số góc đặc biệt ta có: AD AD AD2
Ta có: tan B ;tanC tan B.tanC (1) 
 BD CD BD.CD
 H· BD C· AD (cùng phụ với ·ACB);H· DB ·ADC 900 
 DH BD
Do đó BDH : ADC(g.g) , do đó:
 DC AD
 BD.DC DH.AD (2). Từ (1) và (2) suy ra :
 AD2 AD HD 1
 tan B.tanC 3 . Theo giả thiết , suy ra:
 DH.AD DH AH 2
 HD 1 HD 1
 hay AD 3HD. Thay vào (3) ta được:
 AH HD 2 1 AD 3
 3HD
 tan B.tanC 3 
 DH
 C. BÀI TẬP TỰ LUYỆN. (cứ 10 bài giải 1 lần)
 12
Bài 1. Biết sin .cos . Tính sin ,cos 
 25
Bài 2. Cho tam giác ABC có AB 16, AC 14 và Bµ 600 
 a) Tính độ dài cạnh BC
 b) Tính diện tích tam giác ABC 
Bài 3.Cho tam giác ABC có BC a, µA và hai đường trung tuyến BM ,CN vuông góc 
với nhau. Tính S ABC
Bài 4.Cho tam giác ABC.Gọi lA,lB ,lC lần lượt là độ dài các đường phân giác góc 
 A,B,C . Chứng minh rằng
 2bc A
 a. l cos
 A b c 2
 A B C
 cos cos cos 1 1 1
 b. 2 2 2 
 lA lB lC a b c
 1 1 1 1 1 1
 c. 
 lA lB lC a b c
Bài 5.Cho tam giác ABC.Gọi ma ,mb ,mc lần lượt là độ dài các đường trung tuyến đi qua 
 m m m
 A,B,C,m a b c .Chứng minh rằng:
 2 A
 60
 B H C
 a) Kẻ đường cao AH
Xét tam giác vuông ABH, ta có:
 1
BH AB.cos B AB.cos600 16. 8 
 2
 3
AH AB.sin B AB.sin600 16. 8 3 , áp dụng định lý Pytago vào tam giác vuông 
 2
AHC ta có:
 2
HC 2 AC 2 AH 2 142 8 3 196 192 4 HC 2 
Vậy BC CH HB 2 8 10 
 1 1
 b) S BC.AH .10.8 3 40 3(dvdt) 
 ABC 2 2
Bài 3. A
 E
 F
 B D C
 a) Trước hết chứng minh công thức sin 2sin cos bẳng sử dụng tam giác cân 
 2 2
 tại đỉnh A có µA 2 thông qua công thức diện tích để đi đến kết luạn trên
 1 1 A 1 A
 S bcsin A,S cl sin ,S bl sin
 ABC 2 ABD 2 A 2 ACD 2 A 2
 2bc A
Mà S S S l cos
 ABC ABD ACD A b c 2
 A
 cos
 2 1 b c 1 1
 b) 
 lA 2 bc 2b 2c
 B C
 cos 1 1 1 1
Tương tự 2 ,cos 2 
 lB 2a 2c lC 2a 2b
 A B C
 cos cos cos 1 1 1
 2 2 2 
 lA lB lC a b c
 A B C
 cos cos cos 1 1 1 1 1 1 1 1 1
c. Ta có: 2 2 2 
 lA lB lC lA lB lC lA lB lC a b c
Bài 5. B
 a b C
 x
 A
 d c
 D
Do ABCD nội tiếp nên sin ·ABC sin ·ADC; cos ·ABC cos ·ADC
 1 1
S S S ab cd sin B ab cd 1 cos2 B
 ABCD ABC ADC 2 2
Trong tam giác ABC có AC 2 a2 b2 2abcos B
Trong tam giác ADC có AC 2 c2 d 2 2cd.cos D
 a2 b2 c2 d 2 
 a2 b2 2abcos B c2 d 2 2cd cos D cos B 
 2 ab cd 
 2
 2 2 2 2
 1 1 a b c d 
Do đó S ab cd 1 cos2 B ab cd 1 
 ABCD 2 2 2 ab cd 
 1 2 2 1 2 2 2 2
 4 ab cd a2 b2 c2 d 2 a b c d c d a b 
 4 4 
 a b c d a b c d a b c d a b c d 
 . . . 
 2 2 2 2 
 a b c d
 S p a p b p c p d voi : p 
 ABCD 2 Từ hình vẽ:
 A S A
 r p a tan ABC p a tan 2 
 2 p 2
 2
 S A A A
Từ (1) và (2) ABC p a tan bc.sin cos
 p 2 2 2
 p p a p b p c A A p b p c 
 bc p a sin sin 
 p 2 2 bc
Bài 10.
 a b c a b c a b c a b c 
Theo Hê rông : SABC 
 2 2 2 2 
 a b c 2 a c b 2 a b c a b c a b c a b c 
 a b c a c b a b c a b c b2 c2 a2
Vậy tam giác ABC vuông tại A
Đề bài từ bài 11 đến bài 20
Bài 11.Cho tam giác ABC.Gọi R,r lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp 
 r 1
tam giác. Chứng minh rằng 
 R 2
Bài 12.Cho tam giác ABC.Chứng minh rằng :
 2 2
 cos A cos B 1 2 2
 a) 2 2 cot A cot B 
 sin A sin B 2
 b)3S 2R2 sin3 A sin3 B sin3 C 
 c) p p a p b p c 3p
 1
 d)S 2 a4 b4 c4 
 16
Bài 13.Cho tam giác ABC nhọn có ba cạnh là a,b,c.Chứng minh rằng :
 c2 a2 b2 2ab.cosC AB c,BC a,CA b 
Bài 14. Quan sát hình vẽ , tính N,M của MNL (làm tròn đến phút) a b c
 a) 3
 b c a a c b a b c
 1 1 1 1 hb hc ha 1
 b) c) 2 2 2 
 ha hb hc r ha hb hc r
Bài 18.Cho tam giác ABC có sin2 B sin2 C 2sin2 A . Chứng minh rằng A 60
 4 4 4
Bài 19.Cho tam giác ABC có a 3 b 3 c 3 .Chứng minh rằng có một góc tù 
Bài 20.Tam giác ABC có a2 b2 c2 36r 2 thì có tính chất gì ?
Đáp án từ bài 11 đến bài 20
Bài 11.
 S abc r S 2
Ta có : r ,R 
 p 4S R pabc
 4 p p a p b p c 4 p a p b p c 
 . Mà 
 pabc abc
 2 p a b c
 p a p b 
 2 2
 2 p a c b
 p a p c 
 2 2
 2 p b c a
 p b p c 
 2 2
 abc r 1
 p a p b p c 
 8 R 2
Bài 12.
 2 sin2 A sin2 B 1 1 1 
 a)BDT 2 2 2 2 1
 sin A sin B 2 sin A sin B 
 2 1 1 1 1 1 2 2
 2 2 2 2 4 2 2 sin A sin B 
 sin A sin B 2 sin A sin B sin A sin B Ta có: AHC có H 90 do đó x2 h2 b2 (định lý Pytago ). Mặt khác :
BH 2 AB2 AH 2 hay a x 2 c2 h2 a2 x2 2ax c2 b2 x2 
Hay a2 2ax c2 b2 c2 a2 b2 2ax
Vậy c2 a2 b2 2abcosC
Bài 14.
 L
 30°
 4,2 H
 2
 1
 N
 M 3,8
Kẻ MH  NL tại H 
 ML
Xét MHL có H 90,L 30,ML 4,2 MH 2,1
 2
Và M 2 90 L 60
Xét MNH có MN 3,8cm,MH 2,1,H 90
 MH 2,1
 sin N N 3333'
 ML 3,8
 M1 90 N 90 3333' 5627'
 NML M 2 M1 5627' 60 11627'
Vậy N 3333',M 11627' AH
 BH BD HD 5 3 2cm tan B 2 B 6226'
 BH
Và AB AH 2 BH 2 42 22 2 5cm
AC BC.sin B 10.sin6226' 8,9cm
Bài 17.
 b c a c a b
a) b c a c a b c
 2
 c a b a b c
 c a b a b c a
 2
 b c a b a c
 b c a b a c b
 2
 abc
 a b c a c b b c a abc 1
 a b c a c b b c a 
 a b c a b c
Mà 33 . . 3
 b c a a c b a b c b c a a c b a b c
 1 p a b c
b) p a b c 
 2 S 2S 2S 2S
 1 1 1 1 1 1 1 1
 S 2S 2S 2S
 ha hb hc r
 p a b c
 2 2 2
 2S a 2S b 2S c 1
c) . 
 b 2S c 2S a 2S r
 a2 b2 c2 2S a2 b2 c2
 2 p
 b c a r b c a
 a2 a2
Ta có : a2 b2 2ab b 2a 2a b
 b b
 b2 c2
Tương tự : 2b c, 2c a
 c a
 a2 b2 c2
Cộng lại ta có a b c 2 p
 b c a
Bài 18.
sin2 B sin2 C 2sin2 A b2 c2 2a2