Ôn tập Toán 9 - Chuyên đề 20: Tứ giác nội tiếp

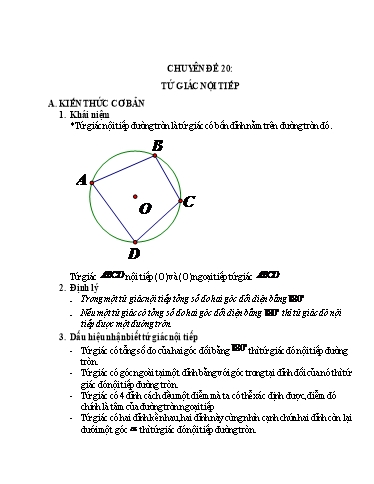
 CHUYÊN ĐỀ 20:
 TỨ GIÁC NỘI TIẾP
A. KIẾN THỨC CƠ BẢN
 1. Khái niệm 
 *Tứ giác nội tiếp đường tròn là tứ giác có bốn đỉnh nằm trên đường tròn đó.
 B
 A
 O C
 D
 Tứ giác ABCD nội tiếp (O) và (O) ngoại tiếp tứ giác ABCD 
 2. Định lý
 - Trong một tứ giác nội tiếp tổng số đo hai góc đối diện bằng 1800 
 - Nếu một tứ giác có tổng số đo hai góc đối diện bằng 1800 thì tứ giác đó nội 
 tiếp được một đường tròn.
 3. Dấu hiệu nhận biết tứ giác nội tiếp
 - Tứ giác có tổng số đo của hai góc đối bằng 1800 thì tứ giác đó nội tiếp đường 
 tròn.
 - Tứ giác có góc ngoài tại một đỉnh bằng với góc trong tại đỉnh đối của nó thì tứ 
 giác đó nội tiếp đường tròn.
 - Tứ giác có 4 đỉnh cách đều một điểm mà ta có thể xác định được, điểm đó 
 chính là tâm của đường tròn ngoại tiếp
 - Tứ giác có hai đỉnh kề nhau, hai đỉnh này cùng nhìn cạnh chứa hai đỉnh còn lại 
 dưới một góc thì tứ giác đó nội tiếp đường tròn. Giải:
 A
 I B'
 O
 C'
 C
 B
 D
 a) Ví dụ 1
 b) Từ câu a B· CB' B· C'B' 1800 (tổng hai góc của tứ giác nội tiếp)
Mà : B· CB' B· DA (hai góc nội tiếp cùng chắn cung AB) 
 B· DI B· C'I 1800 Tứ giác BDIC ' nội tiếp đường tròn (tổng số đo hai góc đối của 
tứ giác bằng 1800 ) 
Ví dụ 3: Cho tam giác ABC vuông tại A, điểm E thuộc BC, kẻ hai trung trực của AB, AC 
gặp nhau ở I. Trung trực của AE cắt hai trung trực kia ở F, K. Chứng minh 5 điểm 
 A,E,F,I,K cùng nằm trên một đường tròn
Giải: B
 A
 C
 D I
 IC AB
Gọi I là trung điểm CD, ta có ICAB là hình bình hành BC AI 1 
 IC / / AB
Tương tự AD BI 2 
 ABCD là hình thang có C D 60 nên ABCD là hình thang cân (3)
Từ (1), (2), (3) ta có hai tam giác ICB,IAD đều hay IA IB IC ID hay bốn điểm 
 A,B,C,Dcùng thuộc một đường tròn
Ví dụ 5. Cho hình thoi ABCD.Gọi O là giao điểm của hai đường chéo. M,N,R,S lần 
lượt là hình chiếu của O trên AB,BC,CD,DA.Chứng minh bốn điểm M,N,R,S cùng 
thuộc một đường tròn. Ví dụ 7. Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I (I 
nằm giữa A và O). Lấy điểm E trên cung nhỏ BC(E khác B và C), AE cắt CD tại F. 
Chứng minh BEFI là tứ giác nội tiếp 
 C E
 F
 A B
 I O
 D
Tứ giác BEFI có BIF 90
 BEF BEA 90(góc nội tiếp chắn nửa đường tròn)
Suy ra tứ giác BEFI nội tiếp đường tròn đường kính BF
 C. BÀI TẬP TỰ LUYỆN. (cứ 10 bài giải 1 lần)
Đề bài từ bài 1 đến bài 10.
Bài 1. Cho đường tròn O và điểm A nằm ngoài đường tròn. Đường thẳng AO cắt 
đường tròn (O) tại điểm thứ hai là B và C ( AB AC). Qua A vẽ đường thẳng không đi 
qua O cắt đường tròn (O) tại hai điểm D và E AB AE . Đường thẳng vuông góc với 
AB tại A cắt CE tại F. M là giao điểm thứ hai của FB với đường tròn (O). Chứng minh 
 DM vuông góc với AC. 
Bài 2. Cho ABC cân ở A nội tiếp (O). Trên tia đối của tia AB lấy điểm M, trên tia đối 
của tia CA lấy điểm N sao cho AM CN. Chứng minh tứ giác AMNO nội tiếp 
Bài 3. Cho tứ giác ABCD nội tiếp (O), M là điểm chính giữa của cung AB. Nối M với D, 
M với C cắt AB lần lượt tại E và P. Chứng minh tứ giác PEDC nội tiếp được đường tròn. Đáp án bài 1 đến bài 10.
Bài 1.
Giải:
 M
 B
 A O C
 D
 E
 F
Ta có B· EC 900 (góc nội tiếp chắn nửa đường tròn)
 B· EF 900 (hai góc kề bù)
Mà B· AF 900 B· AF B· EF 1800 suy ra tứ giác ABEF là tứ giác nội tiếp
 ·AFB ·AEB (hai góc nội tiếp cùng chắn B»D) 
 ·AFB B· MD là cặp góc so le trong AF / / MD 
Lại có AF  AC(gt) DM  AC Bài 3.
 M
 B
 A
 E P
 D O
 C
 sd »AD M»B 
Ta có: M· EP (góc có đỉnh bên trong đường tròn)
 2
 » »
 sd D¼M sd AD MA 
Mà D· CP (góc nội tiếp) hay D· CP 
 2 2
Lại có: ¼AM M»B nên M· EP D· CP 
Nghĩa là tứ giác PEDC có góc ngoài tại đỉnh E bằng góc trong tại đỉnh C 
Vậy tứ giác PEDC nội tiếp được đường tròn. Vậy ta có 9 điểm M ;K;E;P;D;I; N;F;L O;OM dfcm 
Bài 5.
 E
 M
 F
 2
 1 B
 A O K C
Gọi K là giao điểm của đường tròn đi qua ba điểm A,E,F với AB
 µ µ
Nối K với F, ta có: F1 A (cùng bằng nửa số đo KE) 
 µ µ · µ µ
 F2 A (cùng phụ với MBA) F1 F2 K đối xứng với B qua C.
Do B và C là hai điểm cố định nên K cố định
Vậy đường tròn ngoại tiếp tam giác AEF đi qua điểm K cố định. Bài 7.
 A B
 N
 O 2
 M H
 1 2
 1
 D K C
Phần thuận
Ta có CN AM (tính chất đối xứng tâm)
Vì DK DM (gt) nên CK AM CK CN 
Lại có tứ giác MHKD và tứ giác NHKC nội tiếp (vì có hai góc đối vuông)
 ¶ ¶ 0 ¶ ¶ 0 · 0
 M1 H1 45 và N2 H2 45 DHC 90 
Vậy H nằm trên đường tròn đường kính DC 
Giới hạn
Vì đường thẳng xy quay quanh O nhưng phải cắt hai cạnh AD và BC lần lượt tại M và N 
nên điểm H chỉ nằm trên một nửa đường tròn đường kính CD nằm trong hình vuông. Thật vậy,
Lấy E BD sao cho = 
 AD DE
 DAE : CAB(g.g) AD.BC AC.DE (1) 
 AC BC
 BE AB
Tương tự : BAE : CAD(g.g) BE.AC CD.AB (2) 
 CD AC
Từ (1) và (2)
 AD.BC AB.CD AC.DE EB.AC
 AD.BC AB.CD AC.DB(dfcm)
Bài 9.
 B
 E
 O
 A
 D
 C F
Ta có: = 900(AB là tiếp tuyến của (O) tại B); = 900(gt)
 hai đỉnh B và D cùng nhìn đoạn OE dưới một góc vuông.
 Tứ giác EBOA nội tiếp đường tròn 
 = (1) (cùng chắn cung OB)
Chứng minh tương tự ta có:Tứ giác ODCF nội tiếp đường tròn
 퐹 = (2) (góc trong một đỉnh bằng góc ngoài tại đỉnh đối diện Bài 12.Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I (I 
nằm giữa A và O). Lấy điểm E trên cung nhỏ BC (E khác B và C), AE cắt CD tại F. 
Chứng minh : BEFI là tứ giác nội tiếp đường tròn 
Bài 13. Cho tam giác nhọn ABC nội tiếp (O), đường cao BD,CE cắt nhau tại H 
 D AC,E AB . Kẻ đường kính BK, kẻ CP  BK P BK . 
 a) Chứng minh rằng BECD là tứ giác nội tiếp
 b) Chứng minh rằng EDPC là tứ giác nội tiếp, từ đó suy ra ED CP 
Bài 14.Cho điểm A nằm ngoài đường tròn (O). Từ A vẽ các tiếp tuyến AB, AC (B,C là 
các tiếp điểm) và cát tuyến ADE(AD AE). Từ D kẻ đường thẳng vuông góc với OB cắt 
BC, BE lần lượt tại K,H. Chứng minh rằng K là trung điểm của DH.
Bài 15. Cho hình thang ABCD AB / /CD có cạnh bên AD cố định và nội tiếp đường 
tròn (O). Gọi I là giao điểm của hai đường chéo và là đường thẳng qua I song song với 
hai đáy của hình thang. Chứng minh rằng d luôn đi qua một điểm cố định.
Bài 16.Cho nửa đường tròn tâm O đường kính AB,điểm M bất kỳ trên nửa đườngtròn 
 (M khác A,B). Trên nửa mặt phẳng bờ AB chứa nửa đường tròn kẻ tiếp tuyến Ax.Tia 
 BM cắt Ax tại I; tia phân giác của I·AM cắt nửa đường tròn tại E; cắt tia BM tại F,tia 
 BE cắt Ax tại H,cắt AM tại K.Chứng minh rằng: EFMK là tứ giác nội tiếp.
Bài 17.Cho tứ giác ABCD có hai đỉnh B và C ở trên nửa đường tròn đường kính AD,tâm 
O. Hai đường chéo AC và BD cắt nhau tại E. Gọi H là hình chiếu vuông góc của E xuống 
AD và I là trung điểm của DE. Chứng minh rằng:
 a) Các tứ giác ABEH,DCEH nội tiếp được đường tròn
 b) E là tâm đường tròn nội tiếp tam giác BCH
 c) Năm điểm B,C,I,O,H cùng thuộc một đường tròn
Bài 18.Từ một điểm A nằm ngoài đường tròn O;R ta vẽ hai tiếp tuyến AB, AC với đường 
tròn (B, C là tiếp điểm). Trên cung nhỏ BC lấy một điểm M, vẽ MI  AB,
 MK  AC I AB,K AC 
 a) Chứng minh tứ giác AIMK là tứ giác nội tiếp
 b) Vẽ MP  BC P BC .Chứng minh CPMK là tứ giác nội tiếp 
Bài 19.Cho hình vuông ABCD có hai đường chéo cắt nhau tại E. Lấy I AB,M BC sao 
cho IEM 90(I và M không trùng với các đỉnh của hình vuông)
 a) Chứng minh rằng BIEM là tứ giác nội tiếp đường tròn Bài 12.
 E
 C
 F
 A B
 I O
 D
Tứ giác BEFI có BIF 900 (gt),BEF BEA 900 (góc nội tiếp chắn nửa đường tròn)
Suy ra tứ giác BEFI nội tiếp đường tròn đường kính BF.
Bài 13.
 A
 K
 D P
 E O
 H C
 B
Do E,D,P nhìn BC dưới một góc vuông nên B,E,D,P,C nằm trên đường tròn đường 
kính BC. Nên BECD,EDPC là tứ giác nội tiếp. Bài 15.
 A
 B
 K
 I
 d
 O
 D
 C
 sdAD sdBC
Ta có: AID sdAD AOD nên tứ giác OIAD nội tiếp. Vẽ đường tròn 
 2
ngoại tiếp tứ giác OIAD. Do O, A,D cố định nên đường tròn này cố định 
Gọi K là giao điểm của d với đường tròn ngoại tiếp tứ giác OIAD. Ta có 
 AIK ICD IDC DIK nên K là điểm chính giữa của cung AD cố định và do đó K cố 
định. Vậy d luôn đi qua điểm K cố định.