Ôn tập Toán 9 - Chuyên đề 10: Hệ thức lượng giác trong tam giác vuông

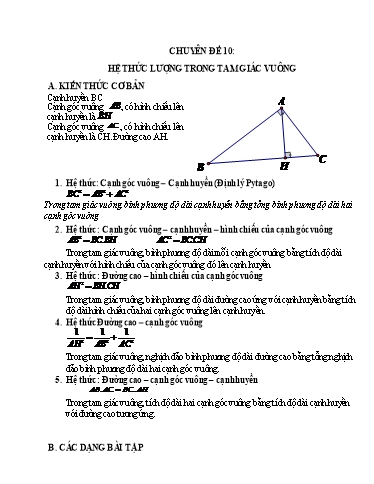
 CHUYÊN ĐỀ 10:
 HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
 A. KIẾN THỨC CƠ BẢN
 Cạnh huyền BC
 Cạnh góc vuông AB , có hình chiếu lên A
 cạnh huyền là BH
 Cạnh góc vuông AC , có hình chiếu lên 
 cạnh huyền là CH. Đường cao AH.
 C
 B H
 1. Hệ thức: Cạnh góc vuông – Cạnh huyền (Định lý Pytago)
 BC 2 AB2 AC 2 
Trong tam giác vuông, bình phương độ dài cạnh huyền bằng tổng bình phương độ dài hai 
cạnh góc vuông
 2. Hệ thức : Cạnh góc vuông – cạnh huyền – hình chiếu của cạnh góc vuông
 AB2 BC.BH AC 2 BC.CH 
 Trong tam giác vuông, bình phương độ dài mỗi cạnh góc vuông bằng tích độ dài 
cạnh huyền với hình chiếu của cạnh góc vuông đó lên cạnh huyền
 3. Hệ thức : Đường cao – hình chiếu của cạnh góc vuông
 AH 2 BH.CH 
 Trong tam giác vuông, bình phương độ dài đường cao ứng với cạnh huyền bằng tích 
 độ dài hình chiếu của hai cạnh góc vuông lên cạnh huyền.
 4. Hệ thức Đường cao – cạnh góc vuông
 1 1 1
 AH 2 AB2 AC 2
 Trong tam giác vuông, nghịch đảo bình phương độ dài đường cao bằng tổng nghịch 
 đảo bình phương độ dài hai cạnh góc vuông.
 5. Hệ thức : Đường cao – cạnh góc vuông – cạnh huyền 
 AB.AC BC.AH 
 Trong tam giác vuông, tích độ dài hai cạnh góc vuông bằng tích độ dài cạnh huyền 
 với đường cao tương ứng.
 B. CÁC DẠNG BÀI TẬP A
 x
 C
 B H M
Ký hiệu như hình bên. Đặt AM x, ta có: BC 2x, AH x 7 
Theo các hệ thức trong tam giác vuông:
 AB2 AC 2 BC 2 4x2 (1)
 AB.AC BC.AH 2x x 7 (2) 
Từ (1) và (2) suy ra:
 AB2 AC 2 2AB.AC 4x2 4x x 7 
 AB AC 2 8x2 28x 72 2x 2 8x2 28x
Đưa về phương trình x2 65x 1296 0 x 16 x 81 0 
Nghiệm dương của phương trình là x 16. Từ đó BC 32cm, AH 9cm 
Vậy diện tích tam giác ABC là: 32.9: 2 144 cm2 
Ví dụ 3. Cho hình thang ABCD có Bµ Cµ 900 , hai đường chéo vuông góc với nhau tại 
H. Biết rằng AB 3 5cm,HA 3cm. Chứng minh rằng:
 a) HA: HB : HC : HD 1: 2: 4:8 
 1 1 1 1
 b) 
 AB2 CD2 HB2 HC 2 A
 7,5 6
 C
 H
 B
 a) Tam giác ABH vuông ở H, theo định lý Pytago, ta có:
 BH 2 AB2 AH 2 7,52 62 20,25 BH 20,25 4,5cm
 Tam giác ABC vuông ở A có AH  BC, theo hệ thức lượng trong tam giác vuông, 
 ta có : 
 AB2 7,52 56,25
 AB2 BH.BC BC 12,5(cm) 
 BH 4,5 4,5
Lại áp dụng định lý Pytago với tam giác vuông ABC, ta có :
 AC 2 BC 2 AB2 12,52 7,52 156,25 56,25 100 AC 100 10(cm) 
Vậy AC 10cm,BC 12,5cm 
 b) Trong tam giác vuông ABC, ta có:
 AB 7,5
 cos B 0,6
 BC 12,5
 AC 10
 cosC 0,8
 BC 12,5
Ví dụ 5. Cho tam giác ABC vuông ở A, có AC 15cm,B 500. Hãy tính độ dài
 a) AB,BC 
 b) Phân giác CD. 
Giải: Ví dụ 6. Cho tam giác ABC, hai đường cao BH,CK 
Chứng minh rằng: nếu AB AC thì BH CK 
 A
 K
 H
 B C
Giả sử AB AC. Trong tam giác vuông AHB,ta có: BH AB.sin A (1) 
Trong tam giác vuông AKC, ta có: CK AC.sinA (2) 
 BK AB.sin A AB
Từ (1) và (2) suy ra : 1 (vì sin A 0, AB AC) do đó BH CK 
 CK AC.sin A AC
 C. BÀI TẬP TỰ LUYỆN. (cứ 10 bài giải 1 lần)
Bài 1. Cho tam giác ABC có đáy BC 2a, cạnh bên bằng b b a 
 a) Tính diện tích tam giác ABC 
 AK
 b) Dựng BK  AC. Tính tỉ số 
 AC
Bài 2. Cho tam giác ABC với các đỉnh A,B,C cà các cạnh đối diện với các đỉnh tương 
ứng là: a,b,c 
 a) Tính diện tích tam giác ABC theo a
 b) Chứng minh a2 b2 c2 4 3S 
Bài 3. Tính diện tích tam giác ABC biết ·ABC 450 , ·ACB 600 , bán kính đường tròn 
ngoại tiếp tam giác ABC là R
Bài 4. Cho tam giác ABC với các đỉnh A,B,C và các cạnh đối diện các đỉnh tương ứng là 
 a,b,c. Chứng minh rằng:
 a) a2 b2 c2 2bccos A Bài 1.
 A
 K
 B H C
 a) Gọi H là trung điểm của BC. Theo định lý Pytago ta có:
 AH 2 AC 2 HC 2 b2 a2 
 1 1
 S BC.AH a b2 a2 AH b2 a2 
 ABC 2 2
 1 1 BC.AH 2a
 b) Ta có : BC BK.AC S BK b2 a2 . Áp dụng định lý 
 2 2 ABC AC b
 Pytago trong tam giác vuông AKB ta có:
 2
 2 2 2
 2 2 2 2 4a 2 2 b 2a 
 AK AB BK b 2 b a 2 . 
 b b
 2 2 2 2
 b 2a AK b 2a
 AK 
 b AC b2
Bài 2. 3
 p a p b p c p3
 p a p b p c . 
 3 27
 2
 p3 p2 a b c 
Suy ra : S p. . hay S . Mặt khác ta dễ dàng chứng minh được
 27 3 3 12 3
 2 2 2
 3 3 a b c 
 a b c 3 a2 b2 c2 S a2 b2 c2 4 3S 
 12 3
Dấu bằng xảy ra khi và chỉ khi ABC đều
Bài 3.
 A
 C B
 H
 D
Dựng các đường thẳng qua C, B lần lượt vuông góc với AC, AB. Gọi D là giao điểm của 
hai đường thẳng trên. Khi đó tam giác ABD, ACD là các tam giác vuông và 4 điểm 
 A,B,C,D cùng nằm trên đường tròn đường kính AD 2R 
 3
Ta có: AB AD.sin600 AD. R 3 . Kẻ đường cao AH H BC. Tức là 
 2
 BC BH CH. Tam giác AHB vuông góc tại H nên 
 AB 2 3 2 R 6
 AH BH ABsin 450 AD. . . Mặt khác tam giác ACH vuông tại 
 2 2 2 2
 R R 1 2 
H nên AC 2 AH 2 CH 2 CH BC 
 2 2
 R2 3 3 
Từ đó tính được diện tích S 
 4 AH h 2h
 sin 2 sin ·AMH . Từ đó suy ra sin 2 2sin cos 
 AM a a
 2
Xét tam giác ABC . Dựng đường cao BE ta có:
 1 1
 S BE.AC BE.b (1) 
 ABC 2 2
Mặt khác trong tam giác vuông AEB 
 BE 1
Ta có: sin A BE c.sin A , thay vào (1) ta có: S absinC 
 AB 2
Trở lại bài toán : 
 A
 2
 1
 C
 B D
 1 µ 1 A 
Ta có: SABD AD.AB.sin A1 AD.c.sin 
 2 2 2 
 1 µ 1 A 
 SACD AD.AC.sin A2 AD.b.sin 
 2 2 2 
 1 A 1
Suy ra SABC SACD SABD AD.sin c b . Mặt khác SABC bcsin A 
 2 2 2
 A
 2bccos
 A bcsin A 2
 ADsin c b bcsin A AD 
 2 A c b
 b c sin 
 2 
Bài 5. Giải: 6 2
Vậy sin750 
 4
Bài 6. 
 A
 M D
 B K C
Tam giác AMB vuông tại M có: MK  AB nên MK 2 AK.BK (1) 
 AHB : CBK vì có: ·AKH C· KB 900;K· AH K· CB (cùng phụ với ·ABC). 
 AK HK
Suy ra do đó: AK.KB CK.KH (2) 
 CK BK
Từ (1) và (2) suy ra MK 2 CK.KH MK CH.HK 
 1 1 1 1
 S AB.MK AB. CK.HK AB.CK. AB.HK S S 
 AMB 2 2 2 2 1 2
Vậy S S1S2 
Bài 7. 2 2
 HB AB2 HB AB 
 2 (2) 
 HC AC HC AC 
 3
 EB AB 
Từ (1) và (2) ta có: 
 FC AC 
 BE BH AB2 AB3
 b) ABC : EBH , thay BH BE (3) 
 BA BC BC BC 2
 AC3
 Tương tự ta cũng có: CF (4) 
 BC 2
 AB3.AC3
 Từ (3) và (4) ta có: BE.CF 
 BC 4
 3 3 3
 AB AC AB.AC 3
Mà AB.AC BC.AH nên BC.BE.CF 2 . 2 .BC AH 
 BC BC BC Bài 10.
 A
 K
 B H C
Đặt BC 2x, từ tính chất của tam giác cân ta suy ra CH x 
Áp dụng định lý Pytago tính được AC 15,62 x2 
 BC KB 2x 2
Từ KBC : HAC hay 
 AC AH 15,62 x2 15,6
Đưa về phương trình 15,62 x2 6,76x2 
Giải phương trình trên ta được nghiệm dương x 6,5 
Vậy BC 2.6,5 13(cm) 
Đề bài từ bài 11 đến bài 20.
Bài 11. Cho hình bình hành ABCD có đường chéo AC lớn hơn đường chéo BD. Kẻ 
 CH  AD ,CK  AB 
 a) Chứng minh CKH : BCA 
 b) Chứng minh HK AC.sin BAD 
 c) Tính diện tích tứ giác AKCH biết B· AD 600 , AB 4cm và AD 5cm. 
Bài 12. Cho tam giác vuông ABC Bµ 900 . Lấy diểm M trên cạnh AC. Kẻ AH  BM , 
 CK  BM.