Ôn tập Chuyên đề Toán Đại 10 - Chương 2, Bài 3: Hàm số bậc hai
Bạn đang xem tài liệu "Ôn tập Chuyên đề Toán Đại 10 - Chương 2, Bài 3: Hàm số bậc hai", để tải tài liệu gốc về máy hãy click vào nút Download ở trên.
Tóm tắt nội dung tài liệu: Ôn tập Chuyên đề Toán Đại 10 - Chương 2, Bài 3: Hàm số bậc hai
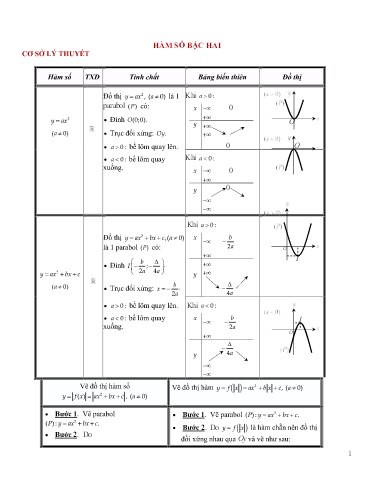
HÀM SỐ BẬC HAI CƠ SỞ LÝ THUYẾT Hàm số TXĐ Tính chất Bảng biến thiên Đồ thị Đồ thị y ax2 , ( a 0) là 1 Khi parabol ()P có: x 0 2 Đỉnh O(0;0). y ax y O (a 0) Trục đối xứng: Oy. 0 a 0: bề lõm quay lên. O a 0: bề lõm quay Khi xuống. 0 0 Khi Đồ thị 2 b y ax bx c,( a 0) là 1 parabol có: 2a O I b Đỉnh I ; y ax2 bx c 24aa b Trục đối xứng: x 4a 2a bề lõm quay lên. Khi bề lõm quay I xuống. O Vẽ đồ thị hàm số Vẽ đồ thị hàm y f x ax2 b x c, ( a 0) y f( x ) ax2 bx c , ( a 0) Bước 1. Vẽ parabol Bước 1. Vẽ parabol ():.P y ax2 bx c Bước 2. Do y f x là hàm chẵn nên đồ thị Bước 2. Do đối xứng nhau qua Oy và vẽ như sau: 1 C. y tăng trên 2; . D. tăng trên ; . Lời giải Chọn A Ta có a 10 nên hàm số tăng trên ;2 và giảm trên nên chọn phương án A. Câu 4. Hàm số nào sau đây nghịch biến trong khoảng ;0 ? A. yx 212 . B. yx 212 . C. yx 21 2 . D. yx 21 2 . Lời giải Chọn A Hàm số nghịch biến trong khoảng nên loại phương án B và D. Phương án A: hàm số nghịch biến trên và đồng biến trên 0; nên chọn phương án A. Câu 5. Cho hàm số: y x2 23 x . Trong các mệnh đề sau, tìm mệnh đề đúng? A. tăng trên . B. giảm trên . C. Đồ thị của có đỉnh I 1;0 . D. tăng trên . Lời giải Chọn D Ta có a 10 nên hàm số giảm trên ;1 và tăng trên 1; và có đỉnh I 1;2 nên chọn phương án D. Vì tăng trên nên tăng trên . Câu 6. Bảng biến thiên của hàm số y 2 x2 4 x 1 là bảng nào sau đây? –∞ 2 +∞ –∞ 2 +∞ 1 +∞ +∞ –∞ –∞ 1 A. . B. . –∞ 1 +∞ –∞ 1 +∞ 3 +∞ +∞ –∞ –∞ 3 C. . D. . Lời giải Chọn C bb Ta có a=-2 <0 và Đỉnh của Parabol I ; f I 1,3 . 22aa Câu 7. Hình vẽ bên là đồ thị của hàm số nào? 1 –1 A. yx 1 2 . B. yx 1 2 . C. yx 1 2 . D. yx 1 2 . Lời giải Chọn B 3 2 4 a .( 2) b .( 2) c 4.ab 2 2 Mặt khác : Vì AIP,() 2 (2) 6 a . 0 b .(0) c c 6 1 a 2 1 Kết hợp (1),(2) ta có : b 2 .Vậy P : y x2 2 x 6. 2 c 6 2 Câu 12. Parabol y ax bx c đi qua A 0; 1 , B 1; 1 ,C 1;1 có phương trình là: A. y x2 x 1. B. y x2 x 1. C. y x2 x 1. D. y x2 x 1. Lời giải Chọn B 2 1 a .0 b .0 c a 1 2 Ta có: Vì ABCP,,() 1 a . 1 b .(1) c b 1 . 2 c 1 1 a . 1 b .( 1) c Vậy P :1 y x2 x . Câu 13. Cho MP : yx 2 và A 2;0 . Để AM ngắn nhất thì: A. M 1;1 . B. M 1;1 . C. M 1; 1 . D. M 1; 1 . Lời giải Chọn A Gọi M P M(,) t t 2 (loại đáp án C, D) Mặt khác: AM t 22 2 t 4 (thế M từ hai đáp án còn lại vào nhận được với sẽ nhận được AM 1 2 2 14 2 ngắn nhất). Câu 14. Giao điểm của parabol P : y x2 54 x với trục hoành: A. 1;0 ; 4;0 . B. 0; 1 ; 0; 4 . C. ; . D. . Lời giải Chọn A x 1 Cho xx2 5 4 0 . x 4 Câu 15. Giao điểm của parabol (P): y x2 32 x với đường thẳng yx 1 là: A. 1;0 ; 3;2 . B. 0; 1 ; 2; 3 . C. 1;2 ; 2;1 . D. ; . Lời giải Chọn A x 1 Cho x22 3 x 2 x 1 x 4 x 3 x 1 . x 3 5 Câu 20. Nếu hàm số y ax2 bx c có đồ thị như sau thì dấu các hệ số của nó là: y A. a 0; b 0; c 0. B. a 0; b 0; c 0. O C. a 0; b 0; c 0. D. a 0; b 0; c 0. x Lời giải Chọn B Nhận xét đồ thị hướng lên nên a 0 . Giao với 0y tại điểm nằm phí dưới trục hoành nên c 0 . Mặt khác Vì và Đỉnh I nằm bên trái trục hoành nên b 0. Câu 21. Cho phương trình: 9m22 – 4 x n – 9 y n – 3 3 m 2 . Với giá trị nào của m và n thì phương trình đã cho là đường thẳng song song với trục Ox ? 2 2 A. mn ;3 B. mn ;3 3 3 2 3 C. mn ;3 D. mn ;2 3 4 Lời giải Chọn C Ta có: Muốn song song với thì có dạng by c 0 , c 0, b 0 2 m 2 3 9m – 4 0 2 n 3 m Nên n2 90 3 . n 3 (nm 3)(3 2) 0 n 3 2 m 3 Câu 22. Cho hàm số f x x2 – 6 x 1 . Khi đó: A. fx tăng trên khoảng ;3 và giảm trên khoảng 3; . B. giảm trên khoảng và tăng trên khoảng . C. luôn tăng. D. luôn giảm. Lời giải Chọn B b Ta có a 10 và x 3 2a Vậy hàm số giảm trên khoảng và tăng trên khoảng . Câu 23. Cho hàm số y x2 – 2 x 3 . Trong các mệnh đề sau đây, tìm mệnh đề đúng? A. y tăng trên khoảng 0; . B. giảm trên khoảng ;2 C. Đồ thị của có đỉnh I 1; 0 D. tăng trên khoảng 1; 7
File đính kèm:
 on_tap_chuyen_de_toan_dai_10_chuong_2_bai_3_ham_so_bac_hai.pdf
on_tap_chuyen_de_toan_dai_10_chuong_2_bai_3_ham_so_bac_hai.pdf

