Chuyên đề Vị trí tương đối trong không gian - Hình học 12

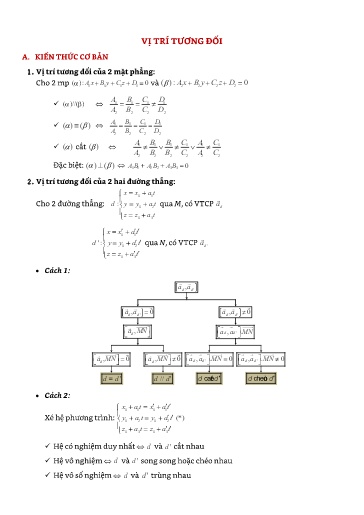
 VỊ TRÍ TƯƠNG ĐỐI 
A. KIẾN THỨC CƠ BẢN 
 1. Vị trí tương đối của 2 mặt phẳng: 
 Cho 2 mp ( ):A1 x B 1 y C 1 z D 1 0 và ( ) :A2 x B 2 y C 2 z D 2 0 
 ABCD
  (  )//( ) 1 1 1 1 
 ABCD2 2 2 2
 ABCD
  ()()  1 1 1 1 
 ABCD2 2 2 2
 ABBCAC
  () cắt () 1 1  1 1  1 1 
 ABBCAC2 2 2 2 2 2
 Đặc biệt: ()()  ABABAB1 1 2 2 3 3 0 
 2. Vị trí tương đối của 2 hai đường thẳng: 
 x x01 a t
 Cho 2 đường thẳng: d: y y02 a t qua M, cĩ VTCP ad 
 z z03 a t
 x x01 a t 
 d': y y02 a t qua N, cĩ VTCP ad ' 
 z z03 a t
 Cách 1: 
 aadd, ' 
 aadd,0'  aadd,0'  
 a, MN add,. a' MN
 d 
 a,0 MN a,0 MN add, a' . MN 0 add, a' . MN 0
 d d 
 dd ' dd// ' ddcắt ' ddchéo '
 Cách 2: 
 x0 a 1 t x 0 a 1 t 
 Xé hệ phương trình: y0 a 2 t y 0 a 2 t (*) 
 z0 a 3 t z 0 a 3 t
  Hệ cĩ nghiệm duy nhất d và d ' cắt nhau 
  Hệ vơ nghiệm d và song song hoặc chéo nhau 
  Hệ vơ số nghiệm d và d ' trùng nhau d I, R : tiếp xúc với ()S . 
 Tiếp điểm J là hình chiếu vuơng gĩc của tâm I lên đường thẳng . 
 AB2
 d I, R : cắt ()S tại hai điểm phân biệt A, B và Rd 2 
 4
B. BÀI TẬP TRẮC NGHIỆM 
Câu 1. Trong khơng gian Oxyz , Cho ba mặt phẳng ( ) :x y 2 z 1 0 ; ( ) :x y z 2 0 ; 
 ( ) :xy 5 0 . Trong các mệnh đề sau, mệnh đề nào sai ? 
 A. (  ) / /( ). B. ()()  . C. ()() . D. ()()  . 
Câu 2. Trong khơng gian , mặt phẳng song song với hai đường thẳng 
 xt 2
 x 21 y z 
 1 :; 2 : yt 3 2 cĩ một vec tơ pháp tuyến là 
 2 3 4 
 zt 1
 A. . n (5; 6;7) B. . n (5; 6; 7) C. n ( 2;6;7) . D. n ( 5; 6;7) . 
Câu 3. Trong khơng gian , cho hai mặt phẳng (P ) :5 x my z 5 0và 
 (Q ) : nx 3 y 2 z 7 0.Tìm mn, để PQ // . 
 3 3
 A. mn ; 10 . B. mn ; 10 . C. mn 5; 3 . D. mn 5; 3 . 
 2 2
Câu 4. Trong khơng gian , cho hai mặt phẳng (P ) : 2 x my 4 z 6 m 0và 
 ():(Q m 3) x y (5 m 1) z 70 . Tìm m để ()()PQ . 
 6
 A. m . B. m 1. C. m 1. D. m 4. 
 5
Câu 5. Trong khơng gian , cho hai mặt phẳng (P ) : 2 x my 2 mz 9 0 và 
 (Q ) :6 x y z 10 0.Tìm m để ()()PQ . 
 A. m 4 . B. m 4. C. m 2. D. m 2 . 
Câu 6. Trong khơng gian , cho hai mặt phẳng (Py ) : 9 0 . Xét các mệnh đề sau: 
 (I) P // Oxz 
 (II) P  Oy 
 Khẳng định nào sau đây đúng: 
 A.Cả (I) và (II) đều sai. B.(I) đúng, (II) sai. 
 C.(I) sai, (II) đúng. D.Cả (I) và (II) đều đúng. 
Câu 7. Trong khơng gian , cho điểm I(2;6; 3) và các mặt phẳng : ( ) :x 2 0;
 ( ) :y 6 0; ( ) :z 3 0 
 A.   . B.  //(Oyz ) . C. ( )//oz . D. qua I . xt 12 xt 2
Câu 15. Trong khơng gian , cho hai đường thẳng d: yt 2 2 và d': y 5 3 t . Trong 
 zt zt 4
 các mệnh đề sau, mệnh đề nào đúng? 
 A. song song. B. trùng nhau. C. chéo nhau. D. cắt nhau. 
 x 21 y z
Câu 16. Trong khơng gianOxyz , cho hai đường thẳng: d : và 
 4 6 8 
 x 72 y z
 d ': . Trong các mệnh đề sau, mệnh đề nào đúng khi nĩi về vị trí 
 6 9 12
 tương đối của hai đường thẳng trên? 
 A. song song. B. trùng nhau. C. chéo nhau. D. cắt nhau. 
 xt 1 12 xt 78
Câu 17. Hai đường thẳng d: y 2 6 t và d : y 6 4 t cĩ vị trí tương đối là:. 
 zt 33 zt 52
 A. trùng nhau. B. song song. C. chéo nhau. D. cắt nhau. 
 xt 1 
 x 1 y 2 z 4 
Câu 18. Trong khơng gian , hai đường thẳng d : và d': y t cĩ 
 2 1 3 
 zt 23 
 vị trí tương đối là: 
 A. trùng nhau. B. song song. C. chéo nhau. D. cắt nhau. 
 x 1 y 2 z 4
Câu 19. Trong khơng gian , cho hai đường thẳng d : . và .
 2 1 3
 xt 1 
 d': y t cắt nhau. Tọa độ giao điểm I của d và d 'là 
 zt 23 
 A. I(1; 2;4) . B. I(1;2;4) . C. I( 1;0; 2) . D. I(6;9;1) . 
Câu 20. Trong khơng gian , cho mặt cầu (S ) : x2 y 2 z 2 4 x 6 y 6 z 17 0 ; và mặt 
 phẳng (P ) : x 2 y 2 z 1 0 . 
 Trong các mệnh đề sau, mệnh đề nào đúng? 
 A. Mặt cầu S cĩ tâm I 2; 3; 3 bán kính R 5 . 
 B. P cắt S theo giao tuyến là đường trịn. 
 C. Mặt phẳng P khơng cắt mặt cầu S . 
 D. Khoảng cách từ tâm của S đến P bằng 1. 
Câu 21. Trong khơng gian , cho mặt cầu S cĩ tâm I 2;1; 1 tiếp xúc với mặt phẳng 
 : 2x 2 y z 3 0 . Mặt cầu S cĩ bán kính R bằng: x 1 y 2 z 3
 và đường thẳng d cĩ phương trình . Phương trình mặt cầu tâm A, 
 2 1 1
 tiếp xúc với d là: 
 A. x 1 2 y 2 2 z 3 2 50 . B. x 1 2 y 2 2 z 3 2 5 2 . 
 C. x 1 2 y 2 2 z 3 2 5 2 . D. x 1 2 y 2 2 z 3 2 50. 
Câu 31. Trong khơng gianOxyz , cho mặt phẳng ba mặt phẳng P : x y z 1 0, 
 Q : 2 x my 2 z 3 0 và R : x 2 y nz 0 . Tính tổng mn 2 , biết rằng PR  
 và PQ // 
 A. 6. B. 1. C. 0. D. 6. 
Câu 32. Trong khơng gian , cho mặt phẳng P : x 2 y 3 z 4 0 và đường thẳng d : 
 x m y2 m z
 . Với giá trị nào của m thì giao điểm của đường thẳng d và mặt 
 1 3 2
 phẳng P thuộc mặt phẳng Oyz . 
 4 12
 A. m . B. m 1. C. m 1. D. m . 
 5 17
 xt 1 
 x 1 y 2 z 4 
Câu 33. Trong khơng gian , cho hai đường thẳng d : và d': y t
 2 1 3 
 zt 23 
 cắt nhau. Phương trình mặt phẳng chứa d và d ' là 
 A. 6x 9 y z 8 0. B. 6x 9 y z 8 0 . 
 C. 2x y 3 z 8 0 . D. 6x 9 y z 8 0. 
 x 7 y 5 z 9
Câu 34. Trong khơng gian , cho hai đường thẳng d : và 
 3 1 4
 x y 4 z 18
 d ': . Phương trình mặt phẳng chứa d và d 'là 
 3 1 4
 A. 63x 109 y 20 z 76 0. B. 63x 109 y 20 z 76 0 . 
 C. 63x 109 y 20 z 76 0 . D. 63x 109 y 20 z 76 0. 
Câu 35. Trong khơng gian , cho mặt phẳng Q song song với mặt phẳng 
 P : 2 x 2 y z 7 0 . Biết mp Q cắt mặt cầu S : x22 ( y 2) z 1 2 25 theo một 
 đường trịn cĩ bán kính r 3. Khi đĩ mặt phẳng Q cĩ phương trình là: 
 A. x y 2 z 7 0. B. 2x 2 y z 17 0 . 
 C. 2x 2 y z 7 0 . D. 2x 2 y z 17 0. 
Câu 36. Trong khơng gian , mặt phẳng P chứa trục Ox và cắt mặt cầu
 (S ) : x2 y 2 z 2 2 x 4 y 2 z 3 0 theo giao tuyến là đường trịn cĩ bán kính bằng 3 
 cĩ phương trình là: