Chuyên đề Vị trí tương đối giữa các điểm, đường thẳng, mặt phẳng - Hình học 12

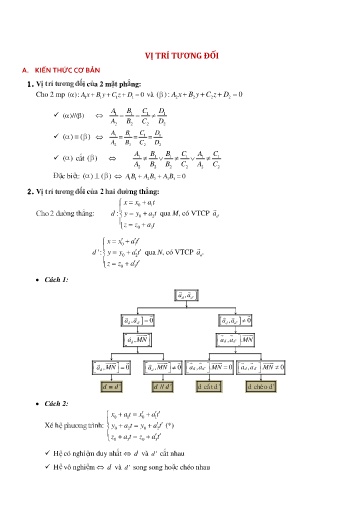
 VỊ TRÍ TƯƠNG ĐỐI
A. KIẾN THỨC CƠ BẢN
 1. Vị trí tương đối của 2 mặt phẳng:
 Cho 2 mp ( ) :A1 x B 1 y C 1 z D 1 0 và ( ) :A2 x B 2 y C 2 z D 2 0
 ABCD
  ( )//(  ) 1 1 1 1
 ABCD2 2 2 2
 ABCD
  ()()   1 1 1 1
 ABCD2 2 2 2
 ABBCAC
  () cắt () 1 1  1 1  1 1
 ABBCAC2 2 2 2 2 2
 Đặc biệt: ()()   ABABAB1 1 2 2 3 3 0
 2. Vị trí tương đối của 2 hai đường thẳng:
 x x0 a 1 t
 Cho 2 đường thẳng: d: y y0 a 2 t qua M, cĩ VTCP ad
 z z0 a 3 t
 x x0 a 1 t 
 d': y y0 a 2 t qua N, cĩ VTCP ad '
 z z0 a 3 t 
 Cách 1:
 ad, a d ' 
 ad, a d '  0 ad, a d '  0
   
 a, MN ad,. a d ' MN
 d 
     
 a, MN 0 a, MN 0 ad, a d ' . MN 0 ad, a d ' . MN 0
 d d 
 d d ' d// d ' dcắt d ' dchéo d '
 Cách 2:
 x0 a 1 t x 0 a 1 t 
 Xé hệ phương trình: y0 a 2 t y 0 a 2 t (*)
 z0 a 3 t z 0 a 3 t 
  Hệ cĩ nghiệm duy nhất d và d ' cắt nhau
  Hệ vơ nghiệm d và d ' song song hoặc chéo nhau Để xét vị trí tương đối giữa và ()S ta tính d I, rồi so sánh với bán kính R .
  d I, R : khơng cắt ()S
  d I, R : tiếp xúc với ()S .
 Tiếp điểm J là hình chiếu vuơng gĩc của tâm I lên đường thẳng .
 AB2
  d I, R : cắt ()S tại hai điểm phân biệt A, B và R d 2 
 4
B. BÀI TẬP TRẮC NGHIỆM
Câu 1. Trong khơng gian Oxyz , Cho ba mặt phẳng ( ) :x y 2 z 1 0 ; ( ) :x y z 2 0 ;
 ( ) :x y 5 0 . Trong các mệnh đề sau, mệnh đề nào sai ?
 A. ( ) / /(  ) . B. ()()   . C. ()()  . D. ()()   .
 x 2 y 1 z
Câu 2. Trong khơng gian Oxyz , mặt phẳng song song với hai đường thẳng :; 
 1 2 3 4
 x 2 t
 2 : y 3 2 t cĩ một vec tơ pháp tuyến là
 z 1 t
 A. . n (5; 6;7) B. . n (5; 6; 7) C. n ( 2;6;7) . D. n ( 5; 6;7) .
Câu 3. Trong khơng gian Oxyz , cho hai mặt phẳng (P ) : 5 x my z 5 0 và (Q ) : nx 3 y 2 z 7 0
 .Tìm m, n để PQ // .
 3 3
 A. m ; n 10 . B. m ; n 10 . C. m 5; n 3 . D. m 5; n 3 .
 2 2
Câu 4. Trong khơng gian Oxyz , cho hai mặt phẳng (P ) : 2 x my 4 z 6 m 0 và
 ():(Q m 3) x y (5 m 1) z 70 . Tìm mđể ()()PQ .
 6
 A. m . B. m 1. C. m 1. D. m 4 .
 5
Câu 5. Trong khơng gian Oxyz , cho hai mặt phẳng (P ) : 2 x my 2 mz 9 0 và (Q ) : 6 x y z 10 0
 .Tìm m để ()()PQ .
 A. m 4 . B. m 4 . C. m 2 . D. m 2 .
Câu 6. Trong khơng gian Oxyz , cho hai mặt phẳng (P ) : y 9 0 . Xét các mệnh đề sau:
 (I) P // Oxz 
 (II) P  Oy
 Khẳng định nào sau đây đúng:
 A.Cả (I) và (II) đều sai. B.(I) đúng, (II) sai.
 C.(I) sai, (II) đúng. D.Cả (I) và (II) đều đúng. x 1 y 7 z 3
Câu 14. Trong khơng gian Oxyz , cho hai đường thẳng d : và
 2 1 4
 x 6 y 1 z 2
 d ': . Trong các mệnh đề sau, mệnh đề nào đúng?
 3 2 1
 A. song song. B. trùng nhau. C. cắt nhau. D. chéo nhau.
 x 1 2 t x 2 t
Câu 15. Trong khơng gian Oxyz , cho hai đường thẳng d: y 2 2 t và d': y 5 3 t . Trong các mệnh
 z t z 4 t
 đề sau, mệnh đề nào đúng?
 A. song song. B. trùng nhau. C. chéo nhau. D. cắt nhau.
 x 2 y z 1 x 7 y 2 z
Câu 16. Trong khơng gian Oxyz , cho hai đường thẳng: d : và d ': .
 4 6 8 6 9 12
 Trong các mệnh đề sau, mệnh đề nào đúng khi nĩi về vị trí tương đối của hai đường thẳng trên?
 A. song song. B. trùng nhau. C. chéo nhau. D. cắt nhau.
 x 1 12 t x 7 8 t
Câu 17. Hai đường thẳng d: y 2 6 t và d : y 6 4 t cĩ vị trí tương đối là:.
 z 3 3 t z 5 2 t
 A. trùng nhau. B. song song. C. chéo nhau. D. cắt nhau.
 x 1 t
 x 1 y 2 z 4 
Câu 18. Trong khơng gian Oxyz , hai đường thẳng d : và d': y t cĩ vị trí
 2 1 3 
 z 2 3 t
 tương đối là:
 A. trùng nhau. B. song song. C. chéo nhau. D. cắt nhau.
 x 1 t
 x 1 y 2 z 4 
Câu 19. Trong khơng gian Oxyz , cho hai đường thẳng d : . và . d': y t
 2 1 3 
 z 2 3 t
 cắt nhau. Tọa độ giao điểm I của d và d 'là
 A. I (1; 2;4) . B. I (1;2;4) . C. I ( 1;0; 2) . D. I (6;9;1) .
Câu 20. Trong khơng gian Oxyz , cho mặt cầu (S ) : x2 y 2 z 2 4 x 6 y 6 z 17 0 ; và mặt phẳng
 (P ) : x 2 y 2 z 1 0 .
 Trong các mệnh đề sau, mệnh đề nào đúng?
 A. Mặt cầu S cĩ tâm I 2; 3; 3 bán kính R 5 .
 B. P cắt S theo giao tuyến là đường trịn.
 C. Mặt phẳng P khơng cắt mặt cầu S .
 D. Khoảng cách từ tâm của S đến P bằng 1. A. x 1 2 y 2 2 z 3 2 9 . B. x 1 2 y 2 2 z 3 2 10 .
 C. x 1 2 y 2 2 z 3 2 10 . D. x 1 2 y 2 2 z 3 2 10 .
Câu 30. Trong khơng gian Oxyz , Trong khơng gian với hệ toạ độ Oxyz, cho điểm I 1; 2;3 và đường
 x 1 y 2 z 3
 thẳng d cĩ phương trình . Phương trình mặt cầu tâm A, tiếp xúc với d là:
 2 1 1
 A. x 1 2 y 2 2 z 3 2 50 . B. x 1 2 y 2 2 z 3 2 5 2 .
 C. x 1 2 y 2 2 z 3 2 5 2 . D. x 1 2 y 2 2 z 3 2 50 .
Câu 31. Trong khơng gian Oxyz , cho mặt phẳng ba mặt phẳng P : x y z 1 0,
 Q : 2 x my 2 z 3 0 và R : x 2 y nz 0 . Tính tổng m 2 n , biết rằng PR  và
 PQ // 
 A. 6. B. 1. C. 0. D. 6.
Câu 32. Trong khơng gian Oxyz , cho mặt phẳng P : x 2 y 3 z 4 0 và đường thẳng d :
 x m y 2 m z
 . Với giá trị nào của m thì giao điểm của đường thẳng d và mặt phẳng P 
 1 3 2
 thuộc mặt phẳng Oyz .
 4 12
 A. m . B. m 1. C. m 1. D. m .
 5 17
 x 1 t
 x 1 y 2 z 4 
Câu 33. Trong khơng gian Oxyz , cho hai đường thẳng d : và d': y t cắt
 2 1 3 
 z 2 3 t
 nhau. Phương trình mặt phẳng chứa d và d ' là
 A. 6x 9 y z 8 0 . B. 6x 9 y z 8 0 .
 C. 2x y 3 z 8 0 . D. 6x 9 y z 8 0 .
 x 7 y 5 z 9 x y 4 z 18
Câu 34. Trong khơng gian Oxyz , cho hai đường thẳng d : và d ': .
 3 1 4 3 1 4
 Phương trình mặt phẳng chứa d và d 'là
 A. 63x 109 y 20 z 76 0 . B. 63x 109 y 20 z 76 0 .
 C. 63x 109 y 20 z 76 0 . D. 63x 109 y 20 z 76 0 .
Câu 35. Trong khơng gian Oxyz , cho mặt phẳng Q song song với mặt phẳng P : 2 x 2 y z 7 0 .
 2
 Biết mp Q cắt mặt cầu S : x2 ( y 2) 2 z 1 25 theo một đường trịn cĩ bán kính r 3.
 Khi đĩ mặt phẳng Q cĩ phương trình là:
 A. x y 2 z 7 0 . B. 2x 2 y z 17 0 .
 C. 2x 2 y z 7 0 . D. 2x 2 y z 17 0 .