Chuyên đề Ứng dụng tích phân để tính diện tích hình phẳng - Đại số 12

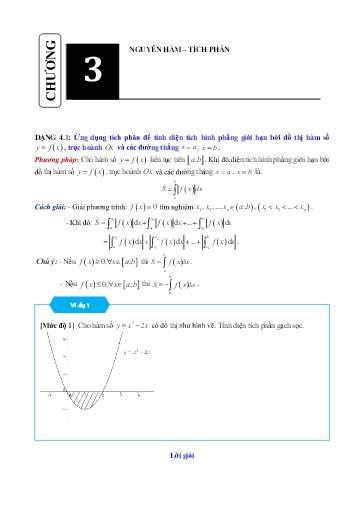
 NGUYÊN HÀM – TÍCH PHÂN 
 3 
 CHƯƠNG
DẠNG 4.1: Ứng dụng tích phân để tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 
 y f x , trục hoành Ox và các đường thẳng xa , xb . 
Phương pháp: Cho hàm số y f x liên tục trên ab, . Khi đó,diện tích hình phẳng giới hạn bởi 
đồ thị hàm số , trục hoành và các đường thẳng , là: 
 b
 S f x dx 
 a
Cách giải: - Giải phương trình: fx 0 tìm nghiệm x12, x ,..., xn a ; b , x12 x ... xn . 
 x x b
 - Khi đó: S 12 f x d x f x d x ... f x d x 
 a x x
 1 n
 x x b
 12f x d x f x d x ... f x d x . 
 a x x
 1 n
 b
 Chú ý: - Nếu f x 0,  x  a ; b thì S f x d x . 
 a
 b
 - Nếu f x 0,  x  a ; b thì S f x d x . 
 a
 Ví dụ 1 
 [Mức độ 1] Cho hàm số y x2 2 x có đồ thị như hình vẽ. Tính diện tích phần gạch sọc. 
 Lời giải 
 Ví dụ 4 
 [Mức độ 2] Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số yx e1x và trục hoành. 
 Lời giải 
 x x 0
Xét phương trình hoành độ giao điểm: x e 1 0 . 
 x 1
 11
Diện tích hình phẳng cần tìm là: S x exx 1 d x x e 1 d x 
 00
 u x dd u x
Đặt xx 
 dv e 1 d x v e x
 1 2
 x11 x x x 1
Khi đó: S x e 11 e x dx e e 
 000 22
 Ví dụ 5 
 [Mức độ 2] Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số yx cos2 , đường thẳng 
 x , trục tung và trục hoành. 
 4
 Lời giải 
Diện tích hình phẳng cần tìm là: 
 44 
 2 1 cos2xx 1 2
S cos x d x d x sin 2 x 4 
 2 2 4 8
 00 0
 II HỆ THỐNG BÀI TẬP TỰ LUẬN. 
 = 
 =
 =I 
Diện tích hình phẳng cần tìm là : 
 00x x
 e1 x d 1 x e 0 1
S d x ln 1 x ex ln 1 . 
 xx 1
 111 xx e 1 e e
 Câu 4 
 sin x
 [Mức độ 2] Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y , đường thẳng 
 1 cos 2x
 x , trục tung và trục hoành. 
 4
 y f x Ox xa xb 
 Lời giải 
Xét phương trình: , . 
 sinx 0 x k k 
 44sinxx sin 1 1 2
Diện tích hình phẳng là: S d x d x ln cos x 4 ln . 
 1 c os2 x 2 cos x 2 2 2
 00 0
DẠNG 4.2: Ứng dụng tích phân để tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 
 , trục hoành và các đường thẳng , . 
Phương pháp: Để tính diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục hoành 
và các đường thẳng , . Ta thực hiện các bước sau: 
 b
Bước 1: Gọi S là diện tích hình phẳng ta có: S f x d x . 
 a
Bước 2: Xét dấu biểu thức fx trên đoạn ab;  . 
Từ đó phân được đoạn ab; thành các đoạn nhỏ, giả sử: a; b  a ; c1  c 1 ; c 2   ...  ck ; b, 
trên mỗi đoạn chỉ có một dấu. 
 c1 b
Bước 3: Khi đó S f x d x ... f x d x . 
 ack
 Câu 3 
 [Mức độ 2] Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số yx log3 , trục Ox và đường 
 thẳng x 9 . 
 Lời giải 
 logxx 0 1
Ta có 3 và log3 x 0 ,  x 1;9 nên diện tích cần tìm là: 
 99
S | log x |d x log x d x .
 1133 
 1
 ux log3 ddux 
Đặt xln 3 . 
 ddvx 
 vx 
 9
 9 1 1 8
Ta có: S x.log31 x | dx 18 0 9 1 18 . 
 1 ln3 ln3 ln3
 Câu 4 
 [Mức độ 2] Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y 3x , trục Ox , trục Oy và 
 đường thẳng x 2 ? 
 Lời giải 
 x
 2 38
Ta có diện tích cần tìm là: Sx 3x d |2 .
 0 ln 30 ln 3 
 Câu 5 
 [Mức độ 2] Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số yx sin 1, trục hoành và hai 
 7 
 đường thẳng x 0 và x . 
 6
 Lời giải 
 7 
Ta thấy sinx 1 0,  x 0; nên diện tích S cần tìm bằng: 
 6
 77 7 7 3 7 
S 66sin x 1d x sin x 1 d x cos cos0 0 1. 
 00 6 6 2 6
 III HỆ THỐNG BÀI TẬP TỰ LUYỆN. 
 === 
 I 
Câu 1: [mức độ 1] Cho hàm số y f x có đồ thị như hình vẽ dưới đây. Diện tích hình phẳng 
 (phần tô màu trong hình vẽ) được tính bằng công thức nào? 
Câu 4: [Mức độ 2] Tính diện tích S của hình phẳng giới hạn bởi các đường y ex , y 2 , x 0 , 
x 1. 
 A. S 4ln2 e 5. B. S 4ln 2 e 6. C. S e72 . D. S e3. 
 Lời giải 
 Chọn A 
 1
 Gọi S là diện tích cần tìm. Ta có Sx ex 2 d . 
 0
 Xét ex 2 0 x ln2 . 
 Bảng xét dấu e2x : 
 x 0 ln 2 1
 x
 e2 0 
 1 ln 2 1
 ln2 1
 Ta có Sx ex 2 d exx 2 dxx e 2 d 2xx exx e 2 
 0 ln2
 0 0 ln 2
 4ln2 e 5 . Vậy S 4ln2 e 5. 
Câu 5: [Mức độ 2] Diện tích hình phẳng được giới hạn bởi đồ thị hàm số yxcos 2 , trục hoành và 
hai đường thẳng xx0, là x, x ,..., x a ; b x x ... x 
 2 12 n 12 n
 A. 2 . B. 1. C. 3 . D. 4 . 
 Lời giải 
 Chọn B. 
 Ta có cos2xx 0 0; . 
 42
 2 4 2 1142
 Nên Scos 2 x d x cos 2 x d x cos 2 x d x sin 2 x sin 2 x 1 .
 00 220
 4 4 
DẠNG 4.3: Ứng dụng của tích phân để tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm 
số y f x và y g x 
Phương pháp giải cơ bản 
Diện tích hình phẳng giới hạn bởi hai đồ thị: C1 : y f x , C2 : y g x và hai đường thẳng 
 b
x a, x b được xác định bởi công thức: S f x g x d x .
 a 
Chú ý: Để phá bỏ dấu giá trị tuyệt đối ta thường làm như sau: 
-Giải phương trình: f x g x tìm nghiệm , . 
 x x b
- Tính: S 12 fxgxx d fxgxx d ... fxgxx d 
 a x x
 1 n
 xb
 1 f x g x d x ... f x g x d x . 
 ax 
 n
Ngoài cách trên, ta có thể dựa vào đồ thị để khử dấu giá trị tuyệt đối.