Chuyên đề Tứ giác - Bồi dưỡng HSG Toán 8

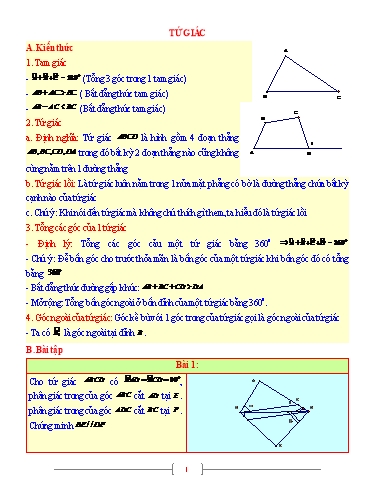
 TỨ GIÁC
A. Kiến thức A
1. Tam giỏc 
- àA Bà +Cà = 1800 (Tổng 3 gúc trong 1 tam giỏc) 
- AB AC BC ( Bất đẳng thức tam giỏc)
 B C
- AB AC BC (Bất đẳng thức tam giỏc)
 C
2. Tứ giỏc B
a. Định nghĩa: Tứ giỏc ABCD là hỡnh gồm 4 đoạn thẳng 
 1
 AB, BC,CD, DA trong đú bất kỳ 2 đoạn thẳng nào cũng khụng A D
cựng nằm trờn 1 đường thẳng
b. Tứ giỏc lồi: Là tứ giỏc luụn nằm trong 1 nửa mặt phẳng cú bờ là đường thẳng chứa bất kỳ 
cạnh nào của tứ giỏc
c. Chỳ ý: Khi núi đến tứ giỏc mà khụng chỳ thớch gỡ them, ta hiểu đú là tứ giỏc lồi
3. Tổng cỏc gúc của 1 tứ giỏc
- Định lý: Tổng cỏc gúc cảu một tứ giỏc bằng 3600 àA Bà +Cà +Dà = 3600
- Chỳ ý: Để bốn gúc cho trước thỏa món là bốn gúc của một tứ giỏc khi bốn gúc đú cú tổng 
bằng 3600
- Bất đẳng thức đường gấp khỳc: AB BC CD DA
- Mở rộng: Tổng bốn gúc ngoài ở bốn đỉnh của một tứ giỏc bằng 3600.
4. Gúc ngoài của tứ giỏc: Gúc kề bự với 1 gúc trong của tứ giỏc gọi là gúc ngoài của tứ giỏc
 à
- Ta cú B1 là gúc ngoài tại đỉnh B .
B. Bài tập
 Bài 1:
 0
 Cho tứ giỏc ABCD cú Bã AD Bã CD 90 , A
 phõn giỏc trong của gúc ABC cắt AD tại E . 
 E
 1
 phõn giỏc trong của gúc ADC cắt BC tại F . B D
 
 Chứng minh BE / /DF
 C
 1 à ả
Từ (1)(2) B1 B2 (đpcm)
 Bài 4:
 C
Cho tứ giỏc ACBD cú BD là phõn giỏc của E
 2 1
gúc ABC , AD CD, AB AC . Chứng minh B
rằng Bã AD Bã CD 1800
 A 1 D
 Lời giải
 +) Trờn cạnh BC lấy điểm E sao cho BE BA
 à à
 A1 E1 (1)
 ả à
+) BED BAD(cgc) AD ED ED CD ECD cõn tại D E2 C1 (2) . 
 ED DA
 à à à ả 0
Từ (1)(2) A1 C1 E1 E2 180
 Bài 1:
Cho tứ giỏc ABCDD cú: àA: Bà :Cà : Dà E
 5:8:13:10
 1 2
a. Tớnh cỏc gúc của tứ giỏc ABCD
 B
b. AB cắt CD tại E , AD cắt BC tại F . 1
Phõn giỏc gúc AED và gúc AFB cắt nhau tại C
 M 75
O , phõn giỏc gúc AFB cắt CD và AB tại M O N
 1
và N . Chứng minh rằng O là trung điểm 
 A D F
của MN
 Lời giải
a. àA 500 , Bà 800 ,Cà 1300 , Dà 1000
b. ãAED 1800 àA Dà 300 ; ãAFB 1800 àA Bà 500
 ã 0 à à 0 ã 0 0 0 0
EMN 180 F1 B1 75 ; ENM 180 75 30 75 EMN cõn O là trung điểm của MN
 3 HèNH THANG, HèNH THANG CÂN
A. HèNH THANG
 A B B C A B
 D C A D D C
 H1. HèNH THANG H2. THANG VUễNG H3. THANG CÂN
1. Định nghĩa: Hỡnh thang là tứ giỏc cú hai cạnh đối song song.
 ABCD la 
 ABCD là hỡnh thang (đỏy AB,CD ) 
 AB / /CD
+) AB : đỏy nhỏ +) CD : đỏy lớn +) AD, BC : cạnh bờn
Nhận xột
- Nếu một hỡnh thang cú hai cạnh bờn song song thỡ hai cạnh bờn bằng nhau
- Nếu một hỡnh thang cú hai cạnh đỏy bằng nhau thỡ hai cạnh bờn song song và bằng nhau
Dựa vào nhận xột ta cú A
 B
Hỡnh thang ABCD AB / /CD , cú:
+) AD / /BC AD BC; AB CD
 D C
+) AB CD AD / /BC; AD BC
2. Hỡnh thang vuụng là hỡnh thang cú 1 gúc vuụng
B. HèNH THANG CÂN
 A B B C A B
 D C A D D C
 H1. HèNH THANG H2. THANG VUễNG H3. THANG CÂN
1. Định nghĩa
Hỡnh thang cõn là hỡnh thang cú hai gúc kề 1 đỏy bằng nhau
 ABCD (là hỡnhthang)
 ABCD là hỡnh thang cõn (đỏy AB,CD ) 
 à à à à
 C = D hoac A B
 5 Bài 1:
Cho tam giỏc ABC cú trọng tõm G và A
đường thẳng d nằm ngoài tam giỏc. Gọi D , P
E, F, H lần lượt là hỡnh chiếu của A, B,C, D G
 d M
lờn đường thẳng . Chứng minh rằng B C
AD BE CF 3GH
 E
 D
 Q H
 K
 F
 Lời giải
+) Gọi M là trung điểm của BC
+) P là trung điểm của AG
+) K là hỡnh chiếu của M lờn d
Ta cú: BE CF 2MK ; AD GH 2PQ;MK PQ 2GH
2 MK PQ 4GH; BE AD CF 3GH (đpcm).
 Bài 1:
Cho hỡnh thang ABCD AB / /CD , trong đú A B
 2
 2 1
CD BC AD . Hai đường phõn giỏc của hai 1
gúc A và B cắt nhau tại K . Chứng minh 
rằng C, D, K thẳng hàng. 2 1
 D E C
 Lời giải
 à à
Trờn CDD lấy điểm E sao cho CE CB AD DE CBE cõn tại C E1 B1 
 à ả à ả
Mặt khỏc E1 B2 (slt) B1 B2
 à ả ả ả à ả
 ADE cõn tại D A1 E2 mà E2 A2 (slt) A1 A2
 7 Khoảng cỏch từ M đến 3 đỉnh là MA MB MC
Ta cần chứng minh DE DF EF MA MB MC
+) Ta cú hỡnh thang BDME là hỡnh thang cõn ( MD / /BE, Bà Eà Cà 600 ) DE MB
Chứng minh tương tự ta cú: DF MA; EF MC DE DF EF MA MB MC (đpcm).
 Bài 1:
Cho tam giỏc ABC cõn tại A , điểm I thuộc A
đường cao AH, BI giao với AC tại D , CI 1 2
 D E
giao với AB tại E 2
 I
a. Chứng minh rằng AD AE
b. Xỏc định dạng của tứ giỏc BEDC
 1 1
c. Xỏc định I sao cho BE ED DC
 2 2
 C H B
 Lời giải
 à à
a. AIC AIB(cgc) C1 B1 ACE ABD(gcg) AE AD
b. ADE, ACB cõn tại A cú chung gúc A
 1800 Aˆ DE / /BC
 ãADE ãAEB ãACB ãABC dpcm 
 à à
 2 C B
 ả ả
c. DE / /BC B2 D2 . 
 Bà Dả
 1 2 à ả
Để BE ED BED cõn tại E B1 B2 
 ả ả
 B2 D2
 à ả
Chứng minh tương tự: C1 C2
Vậy CE và BD là giao điểm của gúc C và B
Vậy I là giao điểm của 3 đường phõn giỏc của tam giỏc ABC
 9 Mà Chu vi hỡnh thang là 20cm nờn ta cú: a a a 2a 20 a 4
 11 Nếu EA ED; EF / / AB / /CD BF CF
b. Định lý 2: Đường trung bỡnh của hỡnh thang song song với hai đỏy và bằng nửa tổng hai 
đỏy
 1
Ta cú: EF / / AB / /CD và EF AB CD 
 2
3. Mở rộng
- Trong hỡnh thang cú hai cạnh bờn khụng song song, đoạn thẳng nối trung điểm của hai 
đường chộo thỡ song song với hai đỏy và bằng một nửa hiệu hai đỏy
 A B
 M N
 D C
 CD AB
Ta cú: MN / / AB / /CD và MN 
 2
C. BÀI TẬP VẬN DỤNG
 Bài 1:
 Cho tứ giỏc ABCD . Gọi E, K, F lần lượt là 
 B
 trung điểm của AD, BC, AC
 A
 a. Chứng minh EK / /CD, FK / / AB
 E F
 1
 b. So sỏnh EF và (AB CD)
 2 K
 D
 c. Tỡm điều kiện của tứ giỏc ABCD để 3 
 C
 điểm E, F, K thẳng hàng, chứng minh 
 1
 EF= (AB CD)
 2
 Lời giải
 1 1 1
 b. Xột EFK ,cú: EF EK KF= CD AB (AB CD) 
 2 2 2
 c. Để E, F, K thẳng hàng, khi đú EF đồng thời song song với AB,CD . Tức là tứ giỏc ABCD 
 13