Chuyên đề Tính thể tích khối đa diện - Hình học 12

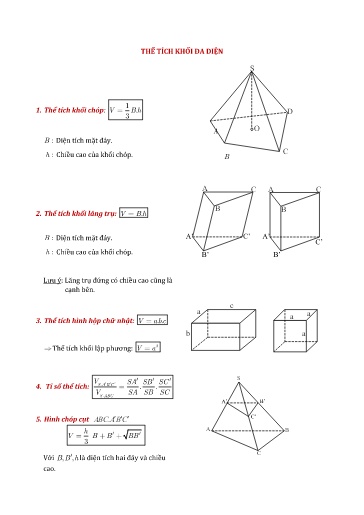
 THỂ TÍCH KHỐI ĐA DIỆN 
 S 
 1
1. Thể tích khối chóp: V B. h D 
 3
 A O 
 B : Diê ̣n tích mă ̣t đắy. 
 C 
 h : Chiều căo củă khói chóp. B 
 A C A C 
 B B 
2. Thể tích khối lăng trụ: V B. h 
 Diê ̣n tích mă ̣t đắy. A’ C’ A’ 
 C’ 
 Chiều căo củă khói chóp. B’ B’ 
 Lưu ý: Lă ng trụ đứng có chiều căo cũng lằ 
 cặnh bê n. 
 c 
 a 
 a a 
3. Thể tích hình hộp chữ nhật: V a.. bc 
 b a 
 Thể tích khói lă ̣p phương: Va3 
 V SA SB SC S 
4. Tỉ số thể tích: SABC. .. 
 VS. ABC SA SB SC 
 A’ B’ 
 C’ 
5. Hình chóp cụt ABC. A B C 
 h A B 
 V B B BB 
 3
 C 
 Với B,, B h lằ diê ̣n tích hăi đắy vằ chiều 
 cao. 2
 SaABCD S
 5a2
 HD2 AH 2 AD 2 
 4
 13aa22 5
 SH SD22 HD a 2 A
 44 D
 12a3 H
 VS. ABCD SH.S ABCD . 
 33 B C 
Câu 4. Cho lăng trụ ABCD.'''' A B C D có ABCD là hình chữ nhật, AAABAD''' . Tính thể tích 
 khối lăng trụ ABCD.'''' A B C D biết AB a , AD a 3 , AA'2 a . 
 A. 3a3 . B. a3 . C. a3 3 . D. 33a3 . 
 Hướng dẫn giải: 
 Gọi O là giăo điểm của AC và BD . 
 ABCD là hình chữ nhật OA OB OD 
 Mà AAABAD nên A' O ABD (vì 
 AO' là trực tâm giác ABD ) 
 ABD vuông tại A 
 22 
 BD AB AD 2 a 
 OA OB OD a 
 AA' O vuông tại O 
 22
 A' O AA ' AO a 3 
 2 
 SABCD AB.3 AD a 
 3
 VABCDA'''' B C D A' O . S ABCD 3 a . 
Câu 5. Lăng trụ tam giác ABC. A B C có đáy tăm giác đều cạnh a , góc giữa cạnh bên và mặt đáy bằng 
 300. Hình chiếu A lên ABC là trung điểm I củă BC . Thể tích khối lăng trụ là 
 a3 3 a3 3 a3 3 a3 3
 A.  B.  C.  D.  
 6 2 12 8
 Hướng dẫn giải: Hướng dẫn giải: S
 Dựng AM CD tại M . 
 Dựng AH SM tại H . 
 36
 Ta có: AH a . 
 4
 AD BC
 S .4 AB a2 
 ABCD 2
 H
 CD AD BC 2 AB2 22 a A D
 1
 S AB. BC a2 M
 ABC 2
 B
 2 C 
 SACD S ABCD S ABC 3 a 
 12S 3 2
 S AM. CD AM ACD a 
 ACD 22CD
 1 1 1AH . AM 3 6
 Ta có: 2 2 2 AS a 
 AH AM AS AM22 AH 2
 1
 V SA. S 2 6 a3 
 S. ABCD3 ABCD
Câu 8. Cho lăng trụ ABCD.'''' A B C D có ABCD là hình thoi. Hình chiếu của A' lên ABCD là 
 trọng tâm của tam giác ABD . Tính thể tích khối lăng trụ ABCA''' B C biết AB a , 
 ABC 1200 , AA' a . 
 a3 2 a3 2 a3 2
 A. a3 2 . B.  C.  D.  
 6 3 2
 Hướng dẫn giải: 
 Gọi H là trọng tâm của tam giác ABD 
 A'
 B '
 A' H ABCD . 
 D ' C '
 Ta có: BAD 18000 ABC 60 . 
 Tam giác ABD cân có BAD 600 
 A
 nên tam giác ABD đều. B
 H
 a 3
 ABD là tăm giác đều cạnh a AH D C 
 3 Dựng tam giác MNP sao cho C, 
 B, D lần lượt là trung điểm các 
 A
 cạnh MN, MP, NP. 
 Do BD là đường trung bình tam 
 1
 giác MNP nên BD MN hay z
 2 x
 11
 1
 AC MN . 20 21
 2 y
 Tam giác AMN vuông tại A (do B
 M P
 có trung tuyến bằng một nửa 21 20
 cạnh tương ứng), hay 11
 C D
 AM AN . Tương tự, 
 AP AN và N 
 AM AP . 
 1 1 1 1
 Ta có SS , SS , SS .Suy ra SS . 
 MBC4 MNP NCD4 MNP BPD4 MNP BCD4 MNP
 xy2 24.20 2
 1 AM AN AP 2 2 2
 Từ đó, VVABCD AMNP . Đặt x ,, y z . Ta có yz 4.21 , 
 4 m m m
 2 2 2
 xz 4.11
 x2 160
 2311
 suy ra y 1440 xyz 1440 VABCD V AMNP 360 m 
 64
 2
 z 324
 1
 (AM, AN, AP đôi một vuông góc nên V AM.. AN AP ) 
 AMNP 6
 2
 V ( a2 b 2 c 2 )( a 2 b 2 c 2 )( a 2 b 2 c 2 ) 
 12
Câu 11. Cho tứ diện S. ABC , M và N là các điểm thuộc các cạnh SA và SB sao cho MA 2 SM , 
 SN 2 NB , () là mặt phẳng qua MN và song song với SC . Kí hiệu ()H1 và ()H2 là các khối 
 đă diện có được khi chia khối tứ diện S. ABC bởi mặt phẳng () , trong đó, ()H1 chứă điểm 
 V1
 S , ()H2 chứă điểm A ; V1 và V2 lần lượt là thể tích của ()H1 và ()H2 . Tính tỉ số . 
 V2
 4 5 3 4
 A. B. C. D. 
 5 4 4 3
 Hướng dẫn giải Gọi J là chân đường cao của hình chóp S
S.ABC; H, K và L lần lượt là hình chiếu của 
J trên các cạnh AB, BC và CA . Suy ra, SHJ , 
SLJ và SKJ lần lượt là góc tạo bởi mặt 
phẳng ()ABC với các mặt phẳng (SAB ), 
()SBC và ()SAC . Theo giả thiết, ta có 
SHJ SLJ SKJ , suy ra các tam giác z=17 K y=9
 C
vuông SJH, SJL và SJK bằng nhau. Từ A
 z=17 J
 y=9
đó, JH JL JK . Mà J nằm trong tam H
 L
giác ABC nên J là tâm đường tròn nội tiếp x=8
tam giác ABC. x=8
 B 
Áp dụng công thức Hê-rông, tă tính được 
diện tích S của tam giác ABC là S 204 . 
Kí hiệu p là nửa chu vi tam giác ABC, r là 
 z K y C
bán kính đường tròn nội tiếp của ABC. Ta A
 S 204
có r 6 . Đặt x BH BL , y
 p 34
 z J
y CL CK , 
 L
 z AH AK . H
 x
 xy 17 x
Ta có hệ phương trình xz 25 . B 
 yz 26
Giải ră được (x ; y ; z ) (8;9;17) 
JB JH2 BH 2 6 2 8 2 10 .Ta có SBJ ( SB ,( ABC )) 45  , suy ra SJB là tam giác 
vuông cân tại J. SJ JB 10 . 
 1
Thể tích V của khối chóp S.ABC là V SJ. S 680 
 3 ABC