Chuyên đề Tính khoảng cách từ một điểm đến đường thẳng, mặt phẳng - Hình học 11

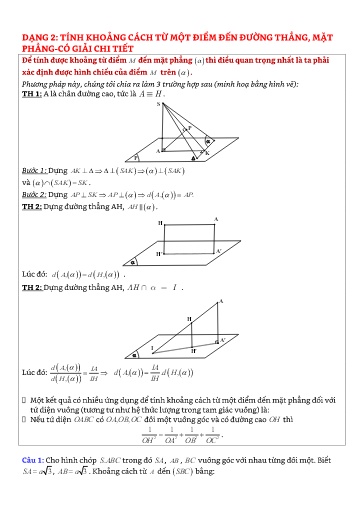
DẠNG 2: TÍNH KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN ĐƯỜNG THẲNG, MẶT 
PHẲNG-CÓ GIẢI CHI TIẾT 
Để tính được khoảng từ điểm M đến mặt phẳng α thì điều quan trọng nhất là ta phải 
xác định được hình chiếu của điểm trên . 
Phương pháp này, chúng tôi chia ra làm 3 trường hợp sau (minh hoạ bằng hình vẽ): 
TH 1: A là chân đường cao, tức là AH. 
 S
 P
 A K
 P 
Bước 1: Dựng AK  SAK  SAK 
và  SAK SK . 
Bước 2: Dựng AP SK AP  d A,. AP 
TH 2: Dựng đường thẳng AH, AH . 
 A
 H
 A'
 H'
Lúc đó: d A , d H , . 
TH 2: Dựng đường thẳng AH, AH I . 
 A
 H
 A'
 I
 H'
 dA , IA IA
Lúc đó: d A , . d H , 
 dH , IH IH
 Một kết quả có nhiều ứng dụng để tính khoảng cách từ một điểm đến mặt phẳng đối với 
 tứ diện vuông (tương tư như hệ thức lượng trong tam giác vuông) là: 
 Nếu tứ diện OABC có OA,, OB OC đôi một vuông góc và có đường cao OH thì 
 1 1 1 1
 . 
 OH2 OA 2 OB 2 OC 2
Câu 1: Cho hình chóp S. ABC trong đó SA , AB , BC vuông góc với nhau từng đôi một. Biết 
SA a 3 , AB a 3 . Khoảng cách từ A đến SBC bằng: 
 a 3
 a 3.
 SO.OM 3 a 3
 OH 3 a . 
 22 3 30 10
 SO OM 3aa22 
 9
Câu 4: Cho tứ diện đều ABCD có cạnh bằng a . Khoảng cách từ A đến BCD bằng: 
 a 6 a 6 a 3 a 3
 A. . B. . C. . D. . 
 2 3 6 3
Hướng dẫn giải: 
Chọn B. 
Ta có: AO BCD O là trọng tâm tam giác BCD. 
 36aa2
d A; BCD AO AB2 BO 2 a 2 . 
 93
Câu 5: Cho hình chóp S. ABCD có đáy là hình thoi tâm O cạnh a và có góc BAD 60o . Đường 
 3a
thẳng SO vuông góc với mặt phẳng đáy ABCD và SO . Khoảng cách từ O đến mặt 
 4
phẳng SBC là: 
 a 3a
A. . B. . C. 
 3 4
3a a 3
 . D. . 
8 4
Hướng dẫn giải: 
 Trong mặt phẳng ABCD: kẻ 
OK BC K BC . 
 Mà BC SO nên suy ra hai mặt phẳng SOK 
và SBC vuông góc nhau theo giao tuyến SK. 
 Trong mặt phẳng SOK : kẻ OH SK H SK . 
 Suy ra: OH SBC d O,. SBC OH 
Câu 6: Cho hai tam giác ABC và ABD nằm trong hai mặt phẳng hợp với nhau một góc 60o , 
 ABC cân ởC, ABD cân ở D. Đường cao DK của bằng12cm . Khoảng cách từ D đến 
 ABC bằng 
Ta có: AB' AC AD ' B ' D ' B ' C CD ' a 2 
Nên tứ diện AB'' CD là tứ diện đều. 
Gọi I là trung điểm BC' , G là trọng tâm tam giác B'' CD . 
Khi đó ta có: d A;'' B CD AG 
 36a
Vì tam giác đều nên D' I a 2. . 
 22
 26a
Theo tính chất trọng tâm ta có: DGDI'' . 
 33 
Trong tam giác vuông AGD' có: 
 2
 2 aa6 2 3
 22 . Chọn C 
 AG D' A D ' G a 2 
 33
Câu 10: Cho hình chóp S. ABC có đáy ABC là tam giác vuông cân tại A với AB a. Mặt bên 
chứa BC của hình chóp vuông góc với mặt đáy, hai mặt bên còn lại đều tạo với mặt đáy một 
góc 45 . Tính khoảng cách từ điểm S đến mặt phẳng đáy ()ABC . 
 a a 2 a 3 3a
 A. . B. . C. . D. . 
 2 2 2 2
Hướng dẫn giải: 
Gọi H là hình chiếu của lên ABC , vì mặt bên SBC 
vuông góc với nên H BC. 
Dựng HI AB, HJ AC , theo đề bài ta có SIH SJH 450 . 
Do đó tam giác SHI SHJ (cạnh góc vuông - góc nhọn) 
Suy ra HI HJ . 
Lại có B C 450 BIH CJH HB HC 
 Vậy trùng với trung điểm của . Từ đó ta có HI là 
 AC a
đường trung bình của tam giác nên HI . 
 22 
Tam giác SHI vuông tại và có SIH 450 SHI vuông 
cân. 
 a
Do đó: SH HI .Chọn đáp án A. 
 2
Câu 11: Cho hình chóp tam giác đều có cạnh bên bằng b, cạnh đáy bằng d , với 
db 3. Hãy chọn khẳng định đúng trong các khẳng định bên dưới. 
 1
 A. d S,() ABC b22 d . B. d S,() ABC b22 d . 
 2
 1
 C. d S,() ABC b22 d . D. d S,() ABC b22 d . 
 3
Hướng dẫn giải: 
 Gọi là trung điểm của , là trọng tâm tam giác . 
 Do S.ABC là hình chóp đều nên SH ABC d S, ABC SH . 
 A. 4.a B. 3.a C. a. D. 2.a 
Hướng dẫn giải: 
 Gọi G là trọng tâm tam giác ABC . Do S. ABC là chóp đều 
nên SG ABC . 
 3a 3 2
 AM AG AM a 3. 
 23
 SAG vuông tại SG SA2 AG 2 4 a 2 3 a 2 a . 
Chọn đáp án C. 
Câu 15: Cho hình chóp tứ giác đều S. ABCD có cạnh đáy bằng 
a và chiều cao bằng a 2 . Tính khoảng cách từ tâm O của đáy ABCD đến một mặt bên: 
 a 3 a 2 2a 5 a 10
 A. . B. . C. . D. . 
 2 3 3 5
Hướng dẫn giải: 
Chọn B. 
SO ABCD , với là tâm của hình vuông 
 . M là trung điểm của CD . 
Kẻ OH SM , ta có: 
 DC SO
 DC  SOM DC  OH . 
 DC MO
nên suy ra d O; SCD OH . 
 1 a
Ta có: OM AD 
 22
 1 1 1 SO.OM 2 a
 2 2 2 OH . 
OH SO OM SO22 OM 3
Câu 16: Cho hình chóp có đáy là n a lục giác đều nội tiếp trong đường tr n 
đường k nh AD 2 a và có cạnh SA vuông góc với mặt phẳng đáy ABCD với SA a 6 . 
Khoảng cách từ A và B đến mặt phẳng SCD l n lượt là: 
 a 2 a 3
 A. a 2 ; B. ; C. a 3 ; D. ; 
 2 2
Hướng dẫn giải: 
 1 1 1 1
 d A, SCD AH ; AH a 2 . 
 AH26 a 2 3 a 2 2 a 2
 12a
 d B,,.,. SCD d I SCD d A SCD 
 22
 Chọn đáp án A. 
Hướng dẫn giải: 
Kẻ HK CD 
 góc giữa hai mặt phẳng SCD và ABCD 
 là SKH 60 
Có HK AD2 a , SH HK.tan60  2 a 3 
Có BC SAB , 
Kẻ HJ SB , mà HJ BC HJ SBC 
d A, SBC BA
 3 
d H, SBC BH
d A, SBC 3. d H , SBC 3 HJ 
 1 1 1 1 1 13
Mà 
 HJ2 HB 2 SH 2 a 212 a 2 12 a 2
 2aa 39 6 39
 HJ d A, SBC . 
 13 13
Chọn C . 
Câu 20: Cho hình chóp S. ABCD có mặt đáy ABCD là hình thoi cạnh a; ABC 120 . Hình 
chiếu vuông góc của đỉnh S lên mặt phẳng là trọng tâm G của tam giác ABD,
ASC 90 . Khoảng cách từ điểm A đến mặt phẳng SBD tính theo a bằng 
 a 3 a 3 a 2 a 6
 A. . B. . C. . D. . 
 6 3 3 3
Hướng dẫn giải: 
Xác định khoảng cách: 
- Đặc điểm của hình: Có đáy là hình thoi, góc 
 nên tam giác ABD đều cạnh 
 a 3
AC a3; AG 
 3
Tam giác SAC vuông ở , có đường cao SG nên 
 a 3 a 6
SA AG. AC . a 3 a ; SG 
 3 3
Xét hình chóp S. ABD có chân đường cao trùng với tâm của đáy nên SA SB SD a . 
- Dựng hình chiếu của lên mặt phẳng : Kẻ đường cao AH của tam giác SAO với O là 
tâm của hình thoi. 
 BD AC
 BD  SAO BD  AH 
 BD SG
 AH BD
 AH SBD . Vậy d A, SBD AH 
 AH SO
- T nh độ dài 
 SG. AO
AH 
 SO