Chuyên đề Tiệm cận của đồ thị hàm số - Đại số 12

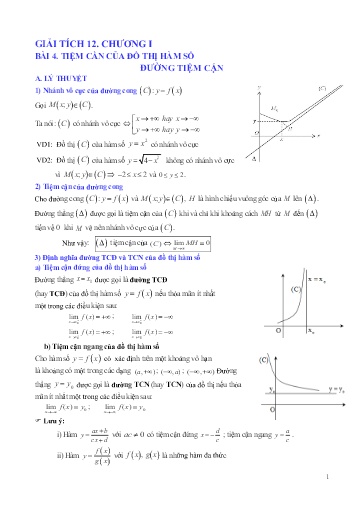
GIẢI TÍCH 12. CHƯƠNG I 
BÀI 4. TIỆM CẦN CỦA ĐỒ THỊ HÀM SỐ 
 ĐƯỜNG TIỆM CẬN 
A. LÝ THUYẾT 
1) Nhánh vô cực của đường cong C : y f x 
Gọi M x; y C . 
 x hay x 
Ta nói: C có nhánh vô cực 
 y hay y 
 2
 VD1: Đồ thị của hàm số yx có nhánh vô cực 
 VD2: Đồ thị của hàm số yx 4 2 không có nhánh vô cực 
 vì 22 x và 02 y . 
2) Tiệm cận của đường cong 
Cho đường cong và , H là hình chiếu vuông góc của M lên . 
Đường thẳng được gọi là tiệm cận của C khi và chỉ khi khoảng cách MH từ M đến 
tiến về 0 khi M vẽ nên nhánh vô cực của C . 
 Như vậy: tiệm cận của ()C limMH 0 
 M 
3) Định nghĩa đường TCĐ và TCN của đồ thị hàm số 
a) Tiệm cận đứng của đồ thị hàm số 
Đường thẳng xx 0 được gọi là đường TCĐ 
(hay TCĐ) của đồ thị hàm số y f x nếu thỏa mãn ít nhất 
một trong các điều kiện sau: 
 limfx ( ) ; limfx ( ) 
 xx 0 xx 0
 limfx ( ) ; limfx ( ) 
 xx 0 xx 0
 b) Tiệm cận ngang của đồ thị hàm số 
Cho hàm số có xác định trên một khoảng vô hạn 
là khoảng có một trong các dạng (,)a ; (,) a ; (,) Đường 
thẳng yy 0 được gọi là đường TCN (hay TCN) của đồ thị nếu thỏa 
mãn ít nhất một trong các điều kiện sau: 
 limf ( x ) y0 ; limf ( x ) y0 
 x x 
 Lưu ý: 
 ax b d a
 i) Hàm y với ac 0 có tiệm cận đứng x ; tiệm cận ngang y . 
 cx d c c
 fx 
 ii) Hàm y với f x , g x là những hàm đa thức 
 gx 
 1 
 Với kết quả này, rõ ràng x 0 không là tiệm cận đứng của đồ thị hàm số. 
  Tìm tiệm cận ngang: Do tập xác định D  9; \ 0;1  nên không 
tồn tại giới hạn khi x dần tới . 
 Xét giới hạn khi x dần tới ta được kết quả như sau: 
 Với kết quả này, ta hiểu rằng limy 0 nên đồ thị hàm số có một tiệm cận 
 x 
ngang là y 0. 
 Vậy ta chọn B. 
MỘT SỐ DẠNG TOÁN 
 DẠNG 1: TÌM TIỆM CẬN CỦA ĐTHS BIẾT BBT CỦA HÀM SỐ, ĐỒ THỊ CỦA HÀM SỐ 
 ĐÓ HOẶC HÀM SỐ LIÊN QUAN 
 Câu 1 
 Cho hàm số có bảng biến thiên 
 Số tiệm cận ngang và đứng của đồ thị hàm số là: 
 Lời giải 
Vì limyy ; lim 3 nên đồ thị hàm số có 1 tiệm cận ngang y 3 
 xx 
Vì lim y nên đồ thị hàm số có 1 tiệm cận đứng xx 
 4
 xx 4
Do đó đồ thị hàm số có tổng số 2 tiệm cận kể cả đứng và ngang. 
 3 
 Câu 4 
 Cho hàm số xác định trên , liên tục trên mỗi khoảng xác định và có bảng biến 
 thiên như sau: 
 Hỏi đồ thị hàm số trên có bao nhiêu đường tiệm cận đứng và ngang? 
 Lời giải 
Tập xác định D \0 . Ta có 
 lim fx ; lim fx do đó đồ thị hàm số không có tiệm cận ngang. 
x x 
limf x x 0 là đường tiệm cận đứng duy nhất của đồ thị hàm số. 
x 0 
 Câu 5 
 Cho hàm số xác định trên , liên tục trên mỗi khoảng xác định và có bảng biến 
 thiên như sau: 
 Tìm các giá trị nguyên của để đồ thị hàm số có 3 đường tiệm cận đứng và 
 ngang? 
 Lời giải 
Tập xác định D \1 . Ta có 
 limf x 2 y 2 là đường tiệm cận ngang. 
x 
limf x x 1 là tiệm cận đứng. 
x 1 
 lim f x m y m là đường tiệm cận ngang. 
x 
Do đó, để đồ thị hàm số có 3 đường tiệm cận thì m 2 , mà m 0;5 nên m 0;1;3;4. 
 5 
Vậy đồ thị 2 đường tiệm cận là: tiệm cận đứng x 1 và tiệm cận ngang y 2 . 
 Câu 8 
 Cho đồ thị hàm số như hình bên. Tìm phương trình các đường tiệm cận đứng và tiệm 
 cận ngang của đồ thị hàm số? 
 Lời giải 
Nhìn vào đồ thị, ta có: lim fx và lim fx . Do đó, đồ thị có một tiệm cận đứng là 
 x 0 x 0 
đường thẳng x 0 . 
Theo đồ thị, ta cũng có: limfx 1 và limfx 1. Do đó, đồ thị có tiệm cận ngang là đường 
 x x 
thẳng y 1. 
Vậy đồ thị có tiệm cận đứng x 0 tiệm cận ngang y 1 
 Câu 9 
 Cho đồ thị một hàm số có hình vẽ như hình dưới đây. 
 Hỏi đồ thị trên có bao nhiêu đường tiệm cận? 
 Lời giải: 
 Nhìn đồ thị ta thấy nhánh bên phải có một tiệm cận đứng, một tiệm cận ngang và nhánh bên 
trái cũng vậy. Tổng cộng có 4 tiệm cận. 
 7 
 Phương pháp giải: Gọi G là đồ thị hàm số y g x . 
 1)Tìm tiệm cận ngang. 
 ux()
 Xét hàm số dạng gx . Một dấu hiệu thường dùng để nhận biết G 
 vx() 
có tiệm cận ngang: 
 + Hàm số y g x xác định trên a; hoặc trên ;a . 
 + Bậc của u(x) Bậc của v(x) . 
 + limg ( x ) y0 hoặc limg ( x ) y0 Đường thẳng yy 0 là tiệm cận 
 x x 
ngang của G . 
 2)Tìm tiệm cận đứng. 
 ux()
 Xét dạng hàm số gx . Một dấu hiệu thường dùng để nhận biết đường thẳng 
 vx()
xx 0 là tiệm cận đứng của : 
 + vx(0 ) 0 và ux(0 ) 0 , gx xác định trên ax; 0 hoặc xb0; . 
 + Ít nhất một trong hai giới hạn limg x , lim g x là giới hạn vô cực. 
 x x00 x x
 xx G
 Đường thẳng 0 là tiệm cận đứng của . 
 Trong chủ đề này, các dấu hiệu nhận biết ở trên dựa vào bảng biến thiên hoặc đồ thị của 
hàm số y f x . 
 Câu 1 
 (Dạng )Cho hàm số có bảng biến thiên như hình dưới đây 
 Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số . 
 Lời giải 
 Dựa vào bảng biến thiên ta có: 
 9 
 1 1
 limgx ( ) lim , limgx ( ) lim Đường thẳng xx 
 1
 x x11 x x 23fx x x11 x x 23fx 
 1
là một tiệm cận đứng của đồ thị hàm số y .
 23fx 
 1 1
 limgx ( ) lim , limgx ( ) lim Đường thẳng
 x x22 x x 23fx x x22 x x 23fx 
xx 2 là một tiệm cận đứng của đồ thị hàm số . 
 1 1
 limgx ( ) lim 0 , limgx ( ) lim 0 Đường thẳng y 0 là 
 xx 23fx xx 23fx 
tiệm cận ngang của đồ thị hàm số . 
 Vậy đồ thị hàm số có 2 đường tiệm cận đứng là ; và 1 tiệm cận 
ngang là . 
 11