Chuyên đề Thể tích (Vận dụng cao) - Ôn thi THPT Quốc gia

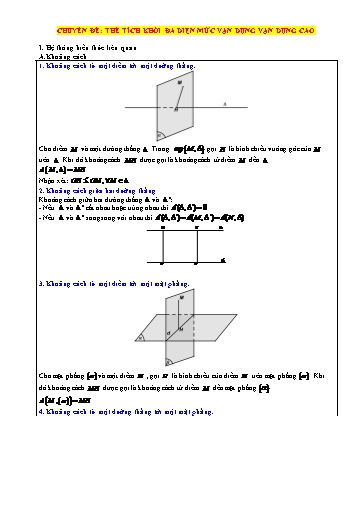
 CHUYấN ĐỀ: THỂ TÍCH KHỐI ĐA DIỆN MỨC VẬN DỤNG VẬN DỤNG CAO
I. Hệ thụng kiến thức liờn quan
A.Khoảng cỏch
1. Khoảng cỏch từ một điểm tới một đường thẳng.
 M
 H
Cho điểm M và một đường thẳng . Trong mp M , gọi H là hỡnh chiếu vuụng gúc của M 
trờn . Khi đú khoảng cỏch MH được gọi là khoảng cỏch từ điểm M đến .
d M , MH
Nhận xột: OH OM ,M 
2. Khoảng cỏch giữa hai đường thẳng 
Khoảng cỏch giữa hai đường thẳng và ' :
- Nếu và ' cắt nhau hoặc trựng nhau thỡ d( , ') 0 .
- Nếu và ' song song với nhau thỡ d( , ') d(M , ') d(N, )
 M K 
 '
 H N
3. Khoảng cỏch từ một điểm tới một mặt phẳng.
 M
 H
 d
 
Cho mặt phẳng α và một điểm M , gọi H là hỡnh chiếu của điểm M trờn mặt phẳng α . Khi 
đú khoảng cỏch MH được gọi là khoảng cỏch từ điểm M đến mặt phẳng α .
d M , α MH 
4. Khoảng cỏch từ một đường thẳng tới một mặt phẳng. 
Phương phỏp 2: Sử dụng tớch vụ hướng: nếu u và v lần lượt là hai vecto chỉ phương ( hoặc vecto 
phỏp tuyến ) của hai đường thẳng a vàb thỡ gúc φ của hai đường thẳng này được xỏc định bởi 
cụng thức
 u.v
 cosφ cos u,v .
 u . v
2.Gúc giữa đường thẳng và mặt phẳng
Nếu đường thẳng a  P thỡ gúc giữa đường thẳng a và P bằng 900 .
Nếu đường thẳng a khụng vuụng gúc với P thỡ gúc giữa đường thẳng a và P là gúc giữa a và 
hỡnh chiếu a của a trờn P .
 a
 a'
 P
3.Gúc giữa hai mặt phẳng
a. Định nghĩa
- Gúc giữa hai mặt phẳng α và β là gúc giữa hai đường thẳng lần lượt vuụng gúc với hai mặt 
phẳng đú.
- Nếu hai mặt phẳng đú song song hoặc trựng nhau thỡ gúc giữa chỳng bằng 0 .
b. phương phỏp tớnh gúc giữa hai mặt phẳng cắt nhau 
 Phương phỏp 1: Dựng hai đường thẳng a , b lần lượt vuụng gúc với hai mặt phẳng α và 
 β . Khi đú, gúc giữa hai mặt phẳng α và β là ãα , β aả,b . Tớnh gúc aả,b .
 Phương phỏp 2: 
 Xỏc định giao tuyến c của hai mặt phẳng α và β .
 Dựng hai đường thẳng a , b lần lượt nằm trong hai mặt phẳng và cựng vuụng gúc với giao 
tuyến c tại một điểm trờn c . Khi đú: ãα , β aả,b .
Hay ta xỏc định mặt phẳng phụ γ vuụng gúc với giao tuyến c mà α  γ a , β  γ b . 
Suy ra ãα , β aả,b . Gọi O là giao điểm của AC và BD ; I A/C /  SO . Suy ra B/ , I, D/ thẳng hàng.
Kẻ AM / / A/C / ;CN / / A/C / . Ta cú: 
 1 1 SA SC SM SN SM SN 2SO
 x z SA/ SC / SI SI SI SI
 1 1 2SO
Chứng minh tương tự ta cũng cú: , Suy ra điều phải chứng minh.
 y t SI
 V
 SA/ B/C/ 1
2)Ta cú V / / / V / / / V / / / x.z.y V / / / xzy.VS.ABCD .
 S.A B C/ D S.A B C S.A D C SA B C
 VSABC 2
 1 1
Chứng minh tương tự ta cú V / / / xzt.VS.ABCD Suy ra V / / / xz(y t) (1)
 SA D C 2 S.A B C/ D 2
 1
Tương tự ta cú V / / / yt(x z) (2)
 S.A B C/ D 2
 xyzt x z y t xyzt 1 1 1 1 
Từ (1) và (2) ta được V / / / .
 S.A B C/ D 4 xz yt 4 x y z t 
Bài toỏn 3: Cho hỡnh lăng trụ tam giỏc ABC.A1B1C1 . Trờn AA1 , BB1 , CC1 lấy lần lượt cỏc điểm 
 AM BN CP V a b c
M , N, P sao cho a , b , c . Khi đú: ABC.MNP 
 AA BB CC V 3
 1 1 1 ABC.A1B1C1
 Lời giải VABCD.MNPQ a 2 b d c VABCD.MNPQ a c b d
Tiếp theo, ta cú .
 V 6 V 2 2
 ABCD.A1B1C1D1 ABCD.A1B1C1D1
II. Cỏc dạng bài tập thường gặp
Dạng I: Tớnh thể tớch khối chúp
1. Vớ dụ minh hoạ 
Vớ dụ 1. Cho hỡnh chúp S.ABCD cú đỏy ABCD là hỡnh vuụng, cỏc mặt bờn SBC , SAD cựng tạo 
với đỏy gúc 60 , mặt bờn SAB vuụng gúc với đỏy. Biết khoảng cỏch từ A đến mặt phẳng SCD 
 21
bằng , tớnh thể tớch khối chúp S.ABC .
 7
 3 3 3 3
A. . B. . C. . D. .
 12 6 8 8
 Lời giải.
ChọnA
 S
 I
 C
 B
 H M
 A D
Hạ SH  AB, H AB , do SAB  ABCD nờn SH  ABCD 
 SH  BC
Cú ABCD là hỡnh vuụng AB  BC
 BC  SAB BC  SB
 SB  BC, BC  AB 
Cú   ABCD , SBC SBH
 SBC  ABCD BC 
(Do SAH 90 )
Chứng minh tương tự  ABCD , SAD SAH
Từ giả thiết suy ra: SAH SBH 60mà H AB suy ra tam giỏc SAB đều và H là trung 
điểm của AB .
Gọi M là trung điểm của CD HM  CD
Cú SH  ABCD SH  CD
 3
 SHM  SCD . Hạ HI  SM thỡ HI  SCD HI 
 12
 1 1 1 1 1 1
Cú 2 2 2 2 2 2 AB 1 (Do AB BC HM )
 HI SH HM 21 AB 3 BC
 7 2 
 1 1 3 1 3
 V SH.S . . .
 S.ABC 3 ABC 3 2 2 12 1 1 a a2 3 a3 3
Thể tớch khối chúp S.ABC là: V SG.S . . 
 3 ABC 3 2 4 24
Chọn đỏp ỏn D. 
Vớ dụ 3. Cho hỡnh chúp S.ABC cú tam giỏc SAB nhọn và nằm trong mặt phẳng vuụng gúc với mặt 
đỏy ABC , tam giỏc ABC vuụng tại C cú AC a, ãABC 30 . Mặt bờn SAC và SBC cựng 
tạo với đỏy gúc bằng nhau và bằng 60 . Thể tớch của khối chúp S.ABC theo a là:
 a3 3a3 2a3 2a3
A. V . B. V . C. V . D. .V 
 2(1 5) 2(1 3) 1 3 2(1 2)
 Hướng dẫn giải
ChọnB.
 S
 P
 A C
 H Q
 30°
 B
+ Theo đề SAB  ABC theo giao tuyến AB . Dựng SH  AB SH  SAB .
 AC
+ ABC vuụng nờn tan30 BC a 3 .
 BC
 1 a2 3
S AC.BC (1) .
 ABC 2 2
 ã ã 0
+ Dựng HP  AC, HQ  BC Sã PH SãQH SAC , ABC SBC , ABC 60 .
 SPH SQH HP HQ .
 HPCQ là hỡnh vuụng. Đặt HQ x,0 x a 3 QB a 3 x .
 QB a 3
 HQB vuụng nờn tan 60 x 3 a 3 x x HQ .
 HQ 3 1
 SH 3a
 SHQ vuụng nờn tan 60 SH (2) .
 HQ 3 1
 3a3
Từ (1) và (2) : V .
 2 3 1 
Vớ dụ 4. Cho khối chúp S.ABC cú đỏy ABC là tam giỏc vuụng cõn tại A , AB a; Sã BA Sã CA 90o
, gúc giữa hai mặt phẳng SAB và SAC bằng 60o . Thể tớch của khối đó cho bằng
 a3 a3 a3
A. a3. B. . C. . D. .
 3 2 6
Lời giải
Chọn D A
 P k
 I
 B N
 M D
 C
Gọi I MN  DC, K AD  PI.
Áp dụng định lý Menelaus cho tam giỏc BCD và3 điểm M , N, I ta cú
 IC ND MB IC 1 IC
 . . 1 .1. 1 3
 ID NB MC ID 3 ID
Áp dụng định lý Menelaus cho tam giỏc ACD và3 điểm P, K, I ta cú
 KD PA IC KD 1 KD 2
 . . 1 . .3 1 
 KA PC ID KA 2 KA 3
 V CP CM CN 2 3 2 1
 CPMN . . . .1 
 V CA CB CN 3 4 4 2
 CABN
 1 1
 V V V (3)
 CPMN 2 CABN 4 ABCD
V AP AK AN 1 3 1
 APKN . . . .1 
VACDN AC AD AN 3 5 5
 VNCPKD 4 4 4 1 2
 VNCPKD VACDN VABCD VABCD (4)
 VACDN 5 5 5 2 5
 13
 3 , 4 V V V V
 CMPKDN CPMN NCPKD 20 ABCD
 V 7
 ABMNKP 
 VCMNDK 13
Vớ dụ 6. Cho hỡnh chúp đều S.ABC cú đỏy là tam giỏc đều cạnh a . Gọi E , F lần lượt là trung điểm 
của cỏc cạnh SB, SC . Biết mặt phẳng (AEF) vuụng gúc với mặt phẳng (SBC) . Tớnh thể tớch khối 
chúp S.ABC .
 a3 5 a3 5 a3 3 a3 6
A. . B. . C. . D. .
 24 8 24 12
 Lời giải
Chọn A
 S
 F
 N
 E
 A C
 O
 M
 B