Chuyên đề Sự tương giao đồ thị hàm số hợp (Phần 2) - Đại số 12

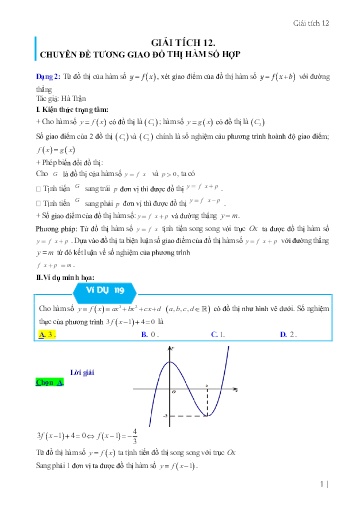
 Giải tích 12 
 GIẢI TÍCH 12. 
 CHUYÊN ĐỀ TƯƠNG GIAO ĐỒ THỊ HÀM SỐ HỢP 
Dạng 2: Từ đồ thị của hàm số y f x , xét giao điểm của đồ thị hàm số y f x b với đường 
thẳng 
Tác giả: Hà Trần 
I. Kiến thức trọng tâm: 
+ Cho hàm số y f x có đồ thị là C1 ; hàm số y g x có đồ thị là C2 
Số giao điểm của 2 đồ thị C1 và C2 chính là số nghiệm cảu phương trình hoành độ giao điểm; 
 f x g x 
+ Phép biến đổi đồ thị: 
Cho G là đồ thị của hàm số y f x và p 0 , ta có 
 G y f x p
 Tịnh tiến sang trái p đơn vị thì được đồ thị . 
 G y f x p
 Tịnh tiến sang phải p đơn vị thì được đồ thị . 
+ Số giao điểm của đồ thị hàm số: và đường thẳng ym . 
Phương pháp: Từ đồ thị hàm số tịnh tiến song song với trục Ox ta được đồ thị hàm số 
 . Dựa vào đồ thị ta biện luận số giao điểm của đồ thị hàm số với đường thẳng
 từ đó kết luận về số nghiệm của phương trình 
 f x p m . 
II.Ví dụ minh họa: 
 Ví DỤ 119
 Ví 
 Cho hàm số y f x ax32 bx cx d a,,, b c d có đồ thị như hình vẽ dưới. Số nghiệm 
 thực của phương trình 3fx 1 4 0 là 
 A. 3 . B. 0 . C. 1. D. 2 . 
 Lời giải 
Chọn A. 
 4
3f x 1 4 0 f x 1 
 3
Từ đồ thị hàm số y f x ta tịnh tiến đồ thị song song với trục 
Sang phải 1 đơn vị ta được đồ thị hàm số y f x 1 . 
 1 | Giải tích 12 
 A. 8 . B. 4 . C. 7 . D. 3. 
 Lời giải 
Chọn B. 
Xét đồ thị hàm số y f x 2019 có được bằng cách tịnh tiến đồ thị hàm số y f x song song 
với trục Ox sang phải 2019 đơn vị. 
Khi đó đồ thị hàm số y f x 2019 gồm hai phần: 
+ Phần đồ thị của hàm số y f x 2019 nằm phía trên trục hoành. 
+ Và phần đối xứng của đồ thị y f x 2019 nằm phía dưới trục hoành. 
 3
Dựa vào đồ thị hàm số y f x 2019 ta thấy: chỉ khi đường thẳng y cắt đồ thị hàm số 
 2
 3
 tại 4 điểm phân biệt nên phương trình fx 2019 có tất cả 4 4 nghiệm 
 2
thực phân biệt. 
 Ví DỤ 122
 Ví 
 Cho hàm số y f x có đồ thị như hình vẽ 
 Hỏi phương trình fx 2018 2019 2020 có bao nhiêu nghiệm thực phân biệt? 
 A. 6 . B. 2 . C. 4 . D. 3 . 
 Lời giải 
Chọn C. 
Xét đồ thị hàm số y f x 2018 2019 có được bằng cách tịnh tiến đồ thị hàm số song 
song với trục sang trái 2018 đơn vị, rồi sau đó tịnh tiến song song với trục Oy xuống dưới 
 2019 đơn vị. 
Ta được đồ thị hàm số y g x f x 2018 2019. 
Khi đó đồ thị hàm số y f x 2018 2019 gồm hai phần: 
+ Phần đồ thị của hàm số y f x 2018 2019 nằm phía trên trục hoành. 
+ Và phần đối xứng của đồ thị y f x 2018 2019 nằm phía dưới trục hoành. 
Dựa vào đồ thị hàm số ta thấy phương trình fx 2018 2019 2020 
có 4 nghiệm thực phân biệt. 
 3 | Giải tích 12 
Hướng 1: Từ Bảng biến thiên hoặc đồ thị hàm số y f() x , sử dụng các phép biến đổi đồ thị ta sẽ 
chuyển được đồ thị hàm số ()C : y f() x sang đồ thị y f() ax b bằng cách như sau: 
Bước 1: Tịnh tiến đồ thị y f() x theo vecto vb ( ;0) ta được (C1 ); 
 1 1
Bước 2: Phép co đồ thị tỉ số k (biến điểm x00;f(x ) thành .;()x00 f x , biến C1 thành C2 
 a a
Khi đó C2 là đồ thị của hàm số y f() ax b . Sau đó biện luận số giao điểm dựa trên đồ thị. 
Lưu ý: 
1. Qua hai phép biến đổi thì đồ thị y f() ax b và đồ thị y f() x đều có cùng số giao điểm với 
đường thẳng có dạng ym . 
2. Qua 2 phép biến đổi đồ thị ta nhận thấy mặc dù điểm cực trị có thể thay đổi nhưng giá trị cực đại 
và cực tiểu của hàm số là không đổi, do đó trong quá trình giải toán, ta hoàn toàn có thể sử dụng giá 
trị cực đại, cực tiểu của hàm số để biện luận. 
Hướng 2: Sử dụng cách đặt ẩn phụ đưa về hàm số theo ẩn mới có chứa y f t . 
 tb 
+ Đặt t ax b( a 0) x . ( tìm điều kiện của t nếu có) 
 a
+ Đưa về hàm số theo ẩn mới có chứa . 
Nhận xét: 
1. với mỗi giá trị của t cho ta một và chỉ một giá trị của x, suy ra số giao điểm của đồ thị hàm số 
 y f t với đường thẳng ym cũng là số giao điểm của đồ thị hàm số y f() ax b với đường 
thẳng . 
2. Hướng giải này phù hợp trong các bài toán tìm m để hai đồ thị cắt nhau tại n điểm thỏa mãn điều 
kiện x  a; b . 
VÍ DỤ MINH HỌA 
 Ví DỤ 124
 Ví 
 Cho hàm số y f x có bảng biến thiên như sau: 
 x 1 1 
 y + 0 0 + 
 0 
 y
 4 
 Số nghiệm thực của phương trình fx 12 là 
 A. 0 . B. 1. C. 3 . D. 2 . 
 Lời giải 
Chọn B 
 5 | Giải tích 12 
 1
Đặt 12 x t t R . Ta có phương trình ft 1 . 
 5
 1
Số nghiệm của phương trình 1 là số giao điểm của đồ thị hàm số y f t và đường thẳng y 
 5
. Ta có bảng biến thiên sau: 
Dựa vào bảng biến thiên ta thấy đường thẳng cắt đồ thị hàm số tại 2 điểm phân 
biệt nên phương trình 1 có 2 nghiệm phân biệt. 
 1 t
Ta có 12 x t x nên ứng với 2 nghiệm t sẽ cho 2 nghiệm x . 
 2
Vậy phương trình ban đầu có 2 nghiệm phân biệt. 
 Ví DỤ 126
 Ví 
 Cho hàm số có bảng biến thiên như sau: 
 y f x 
 Đồ thị hàm số y f 31 x cắt đường thẳng y m2 m tại 3 điểm phân biệt khi: 
 m 2
 A. 21 m B. 12 m C. m 1 D. 
 m 1 
 Lời giải 
Xét phương trình f 31 x m2 m 
Đặt 31x t t R . Ta có phương trình f t m2 m . 
 7 | Giải tích 12 
 m
Phương trình * có 4 nghiệm phân biệt khi 21 42 m . 
 2
 Ví DỤ 128 
 Ví 
 Cho hàm số y f x có bảng biến thiên dưới đây: 
 Để phương trình 3f 2 x 1 m 2 có 3 nghiệm phân biệt thuộc 0;1 thì giá trị của tham số m 
 thuộc khoảng nào dưới đây? 
 A. ;3 B. 1;6 C. 6; D. 3;1 
 Lời giải 
Chọn B 
Đặt tx 21. Ta thấy t là hàm đồng biến theo x và xt 0;1  1;1 . 
 m 2
Do đó phương trình 3f 2 x 1 m 2 có 3 nghiệm phân biệt thuộc 0;1 ft() có 3 
 3
nghiệm phân biệt thuộc  1;1. 
 m 2
Dựa vào bảng biến thiên suy ra 1 m 5. 
 3
 Ví DỤ 129
 Ví 
 Cho hàm số y f x có bảng biến thiên như hình vẽ bên: 
 9 |