Chuyên đề Rèn luyện cho học sinh năng lực giải toán phần quan hệ song song thông qua các bài toán cơ bản

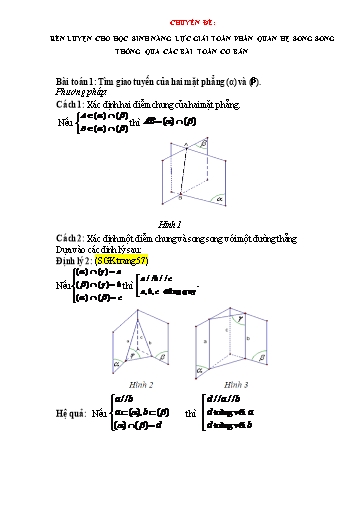
 CHUYÊN ĐỀ: 
RÈN LUYỆN CHO HỌC SINH NĂNG LỰC GIẢI TỐN PHẦN QUAN HỆ SONG SONG 
 THƠNG QUA CÁC BÀI TỐN CƠ BẢN
 Bài tốn 1: Tìm giao tuyến của hai mặt phẳng (α) và ().
 Phương pháp:
 Cách 1: Xác định hai điểm chung của hai mặt phẳng.
 A ( )  ( )
 Nếu thì AB ( )  ( ) 
 B ( )  ( )
 Hình 1
 Cách 2: Xác định một điểm chung và song song với một đường thẳng
 Dựa vào các định lý sau:
 Định lý 2: (SGK trang 57) 
 ( )  ( ) a
 a / /b / /c
 Nếu ( )  ( ) b thì .
 a,b,c đồng quy
 ( )  ( ) c
 a / /b d / /a / /b
 Hệ quả: Nếu a  ( ),b  ( ) thì d a. 
 trùng với 
 ( )  ( ) d d trùng với b * Nhận xét: Để tìm giao tuyến của hai mặt phẳng ta ưu tiên cho cách 1 là tìm hai 
điểm chung lần lượt nằm trên hai mặt phẳng đĩ bằng cách dựa vào hình vẽ. Nếu hình vẽ chỉ 
cĩ một điểm chung thì ta chuyển sang cách hai ( dựa vào các định lý và hệ quả trên)
Ví dụ 1: Trong mp(α) cho tứ giác ABCD cĩ AB và CD cắt nhau tại E, AC và BD cắt nhau 
tại F. Gọi S là một điểm nằm ngồi mp(α). Tìm giao tuyến của:
a) mp(SAC) và mp(SBD) b) mp(SAB) và mp(SCD)
c) mp(SEF) và mp(SAD)
Nhận xét: Với câu a, b học sinh dễ dàng tìm được giao tuyến. 
 Với câu c) GV cần gợi ý cho HS phát hiện ra được điểm chung thứ hai.
 Lời giải:
a) Ta cĩ S (SAC)  (SBD) (1) ; F = AC  BD F (SAC)  (SBD) (2) 
 Từ (1) và (2) suy ra : SF = (SAC)  (SBD).
b) Ta cĩ S (SAB)  (SCD) (1) ; E = AB  CD E (SAB)  (SCD) (2) 
 Từ (1) và (2) suy ra : SE = (SAB)  (SCD).
c) Trong mp(ADE) kéo dài EF cắt AD tại N.
 Xét hai mp(SAD) và (SEF) cĩ: S (SAD)  (SEF); N (SAD)  (SEF) 
 Vậy : SN = (SAD)  (SEF). 
 Ví dụ 2. Cho hình chĩp S.ABCD cĩ đáy ABCD là hình bình hành. Tìm giao tuyến của 
 các mặt phẳng: - Tìm giao tuyến a của hai mp và mp  .(hình 9)
* Nhận xét: Vấn đề của bài tốn là xác định cho được đường thẳng a . Nhiệm vụ của giáo 
viên là hướng dẫn, gợi mở cho học sinh biết cách tìm đường thẳng a và chọn mp  sao 
cho phù hợp với từng yêu cầu của bài tốn trong trường hợp đường thẳng a chưa cĩ trên 
hình vẽ.
Ví dụ 1: Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của AB và AD sao cho 
 2
 AJ AD . Tìm giao điểm của đường thẳng IJ với mp(BCD).
 3
Nhận xét : - HS dễ dàng phát hiện ra đường thẳng a chính là đường thẳng BD.
 - GV cần lưu ý cho học sinh điều kiện để hai đường thẳng cắt nhau là hai đường 
 thẳng phải cùng nằm trên một mặt phẳng và khơng song song.
 Lời giải:
 2 1
Trong ABD cĩ: AJ AD và AI AB , suy ra IJ khơng song song BD. 
 3 2
 K IJ
 Gọi K IJ  BD Vậy K = IJ  (BCD).
 K BD  (BCD)
Ví dụ 2: Cho hình chĩp S.ABCD cĩ đáy ABCD là hình thang (AB // CD). Gọi I, J lần lượt 
 là trung điểm của SA và SB, M là điểm tùy ý thuộc đoạn SD.
 a) Tìm giao điểm của đường thẳng BM với mp(SAC)
 b) Tìm giao điểm của đường thẳng IM với mp(SBC)
 c) Tìm giao điểm của đường thẳng SC với mp(IJM)
 Nhận xét: Câu a) HS dễ nhầm lẫn đường BM cắt SC. Khơng nhìn ra được đường 
thẳng nào nằm trong mp(SAC) để cắt được BM. Trong mp(SAE) cĩ IM cắt SE tại F. Vậy F = IM  (SBC) 
c) Ta cĩ SC  (SBC)
 Xét 2 mp(IJM) và (SBC) ta cĩ : JF = (IJM)  (SBC)
 Trong mp(SBE) cĩ JF cắt SC tại H. Vậy H = SC  (IJM).
Bài tốn 3: Chứng minh quan hệ song song.
 3.1. Chứng minh hai đường thẳng song song.
 Để chứng minh hai đường thẳng a và b song song với nhau trong khơng gian GV cĩ 
thể định hướng và cho học sinh rèn luyện chứng minh theo các cách sau:
 Cách 1: Chứng minh chúng cùng thuộc một mặt phẳng rồi dùng các phương pháp 
chứng minh hai đường thẳng song song trong mặt phẳng.
 Cách 2: Chứng minh hai đường thẳng đĩ cùng song song với đường thẳng thứ ba .
 Cách 3: Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì 
giao tuyến của chúng( nếu cĩ )cũng song song với hai đường thẳng đĩ .
 Cách 4: Sử dụng định lý về giao tuyến của ba mặt phẳng .
 Trong 4 cách nêu trên thì cách 2 và cách 3 hay được sử dụng khi chứng minh 2 đường 
thẳng song song trong khơng gian. Tùy vào bài tốn cụ thể mà ta nên chọn cách chứng minh 
cho phù hợp và hiệu quả. Trong trường hợp hai đường thẳng a và b đồng phẳng ta cĩ thể 
sử dụng các kết quả đã biết trong hình học phẳng để chứng minh .
Ví dụ 1. Cho hình chĩp S.ABCD cĩ đáy ABCD là một hình thang với đáy lớn AB . Gọi 
 M , N lần lượt là trung điểm của SA và SB . Gọi P là giao điểm của SC và ADN 
 , I là giao điểm của AN và DP . Khẳng định nào sau đây là đúng?
 A. SI song song với CD . B. SI chéo với CD .
 C. SI cắt với CD . D. SI trùng với CD .
 (Trích nhĩm giáo viên tốn Việt Nam)
 Hướng dẫn giải:
 Chọn A.
 S I
 N
 M
 A B
 P
 D C
 E
 Trong ABCD gọi E AD  BC , trong SCD gọi P SC  EN . AD  SAD 
 BC  IBC 
Vậy .
 AD//BC
 SAD  IBC PQ
 PQ//AD//BC 1 .
Tương tự J SBC J SBC  ADJ .
 AD  ADJ 
 BC  SBC 
Vậy .
 AD//BC
 SBC  ADJ MN
 MN //AD//BC 2 .
Từ 1 và 2 suy ra MN //PQ .
b) Chọn D.
 S
 P I
 Q
 A
 K
 E D
 M J N F
 B
 C
 E AMND F AMND 
Ta cĩ E AM  BP ; F DN  CQ .
 E PBCQ F PBCQ 
 AD//BC
Do đĩ EF AMND  PBCQ . Mà EF //AD//BC//MN //PQ .
 MN //PQ
Tính EF : Gọi K CP  EF EF EK KF.
 EK PE PE PM
Ta cĩ EK //BC 1 , PM //AB .
 BC PB EB AB
 PM SP 2 PE 2
Mà .
 AB SA 3 EB 3
 EK PE PE 1 2 2 2
Từ 1 suy ra EK BC b.
 EB
 BC PB PE EB 1 5 5 5
 PE
 2 2
Tương tự KF a . Vậy EF EK KF a b .
 5 5 Ở Ví dụ 1 này giáo viên đưa ra ở mức độ đơn giản để chứng minh đường thẳng song 
song với mặt phẳng ta đi chứng minh nĩ song song với 1 đường thẳng dễ nhìn thấy trong 
mặt phẳng. Để giúp học sinh cĩ tư duy tốt hơn ta nâng dần khả năng tìm đường thẳng khĩ 
hơn ở Ví dụ 2, Ví dụ3, Ví dụ4.
Ví dụ 2: Cho hình thang ABCD cĩ AB / /CD và S ABCD . Trên SA,BD lấy hai điểm 
 SM DN 2
 M , N sao cho . Kẻ NI / / AB I AD . Chứng minh MN / / SCD .
 SA DB 3
 Lời giải
 AM 1 AI BN 1
Ta cĩ . Do NI / / AB nên .
 AS 3 AD BD 3
 AM AI
Suy ra MI / /SD MI / / SCD 
 AS AD
Do NI / /AB ta suy ra NI / /CD . 
Vậy MNI / / SCD MN / / SCD .
Ví dụ 3. Cho hình hộp ABCD.A'B'C'D' cĩ tất cả các mặt đều là hình vuơng cạnh a . Các 
điểm M,N lần lượt trên AD',BD sao cho AM DN x 0 x a 2 .
a) Chứng minh khi x biến thiên, đường thẳng MN luơn song song với một mặt phẳng cố 
định.
 a 2
b) Chứng minh khi x thì MN / /A'C .
 3
 Lời giải 3.3. Chứng minh hai mp(α) và mp() song song nhau.
 * Phương pháp: Để chứng minh hai mặt phẳng song song ta cĩ thể thực hiện một 
trong ba hướng sau :
 Cách 1: Chứng minh trong mặt phẳng này cĩ hai đường thẳng cắt nhau cùng song song 
với mặt phẳng kia.
 a,b  (P)
 Nếu a  b I thì (P) // (Q). 
 a / /(Q),b / /(Q)
 Cách 2: Chứng minh hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba.
 Cách 3 :Chứng minh hai mặt phẳng phân biệt khơng cĩ điểm chung.
 * Nhận xét: Tương tự như bài tốn chứng minh đường thẳng song song với mặt 
phẳng, vấn đề đặt ra là chọn hai đường thẳng a,b như thế nào ? Nằm trên mặt phẳng P hay 
mp Q ? GV cần hướng dẫn, gợi mở cho HS phát hiện ra được vấn đề của bài tốn.
Ví dụ 1. Cho hình chĩp S.ABCD cĩ đáy ABCD là hình bình hành tâm O , gọi M,N lần 
lượt là trung điểm của SA,SD . Chứng minh OMN / / SBC .
 Lời giải
 S
 M
 N A
 B
 O
 C
 D
Ta cĩ M,O lần lượt là trung điểm của SA,AC nên OM là đường trung bình của tam 
giác SAC ứng với cạnh SC do đĩ OM / /SC .
 OM / /SC
Vậy OM / / SBC 1 .
 SC  SBC 
Tương tự, Ta cĩ N,O lần lượt là trung điểm của SD,BD nên ON là đường trung bình 
của tam giác SBD ứng với cạnh SBdo đĩ OM / /SB .
 ON PSB
Vậy OM P SBC 2 . Từ 1 và 2 ta cĩ 
 SB  SBC 
 OM / / SBC 
 ON / / SBC OMN / / SBC .
 OM ON O
Ví dụ 2. Cho hai hình vuơng ABCD và ABEF ở trong hai mặt phẳng phân biệt. Trên các 
đường chéo AC và BF lần lượt lấy các điểm M,N sao cho AM BN . Các đường thẳng