Chuyên đề Phân thức đại số (Phần 1) - Bồi dưỡng HSG Toán 8

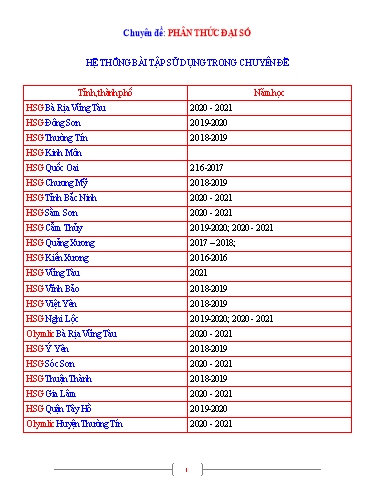
 Chuyên đề: PHÂN THỨC ĐẠI SỐ
 HỆ THỐNG BÀI TẬP SỬ DỤNG TRONG CHUYÊN ĐỀ
 Tỉnh, thành phố Năm học
HSG Bà Rịa Vũng Tàu 2020 - 2021
HSG Đông Sơn 2019-2020
HSG Thường Tín 2018-2019
HSG Kinh Môn
HSG Quốc Oai 216-2017
HSG Chương Mỹ 2018-2019
HSG Tỉnh Bắc Ninh 2020 - 2021
HSG Sầm Sơn 2020 - 2021
HSG Cẩm Thủy 2019-2020; 2020 - 2021
HSG Quảng Xương 2017 – 2018;
HSG Kiến Xương 2016-2016
HSG Vũng Tàu 2021
HSG Vĩnh Bảo 2018-2019
HSG Việt Yên 2018-2019
HSG Nghi Lộc 2019-2020; 2020 - 2021
Olymlic Bà Rịa Vũng Tàu 2020 - 2021
HSG Ý Yên 2018-2019
HSG Sóc Sơn 2020 - 2021
HSG Thuận Thành 2018-2019
HSG Gia Lâm 2020 - 2021
HSG Quận Tây Hồ 2019-2020
Olymlic Huyện Thường Tín 2020 - 2021
 1 x y z 0 x2 y2 z2 2(xy yz zx) (x2 y2 z2 )2 4(xy yz zx)2 (2)
Từ (1)(2) x4 y4 z4 2(x2 y2 y2 z2 z2 x2 ) 4(x2 y2 y2 z2 z2 x2 2xy2 z 2x2 yz 2xyz2 )
 4 x2 y2 y2 z2 z2 x2 2xyz(x y z) =4(x2 y2 y2 z2 z2 x2 ) x4 y4 z4 2(x2 y2 y2 z2 z2 x2 )
  Thay 
 =0 
vào (1), ta được : (x2 y2 z2 )2 2(x4 y4 z4 )
 1
b. VT x5 y5 z5 x2 y2 (x y) x2 z2 (x z) y2 z2 (y z)
 5
 1
Từ x y z 0 x y z; x z y; y z x VT x5 y5 z5 xyz(xy yz zx)(1)
 5
 x2 y2 z2
x y z 0 (x y z)2 0 x2 y2 z2 2(xy yz zx) xy yz zx 
 2
Theo câu a, ta có : x3 y3 z3 3xyz khi x + y + z = 0 
 x2 y2 z2 x3 y3 z3
 (xy yz zx).xyz . (2)
 2 3
Thay vào (1), ta được: 5(x3 y3 z3 )(x2 y2 z2 ) 6(x5 y5 z5 )(*)
c. Ta có : x3 y3 z3 3xyz , thay vào (*) ta được : 
5.3xyz(x2 y2 z2 ) 6(x5 y5 z5 ) 5xyz(x2 y2 z2 ) 2(x5 y5 z5 )(dpcm) 
 Bài 4: Chứng minh rằng
 3 3 3 2 2 2
a. 2(a b c 3abc) (a b c) (a b) (b c) (c a) 
b. (a b)(b c)(c a) 4abc c(a b)2 a(b c)2 b(c a)2
 Lời giải
a. VP (a b c)(a2 b2 c2 ab bc ca)
1
 VT a3 b3 c3 3abc (a b)3 c3 3ab(a b) 3abc (a b)3 c3 3ab(a b c)
2
 2 2 2 2 2
 (a b c) (a b) (a b)c c 3ab (a b c)(a b c ab bc ca) VT VP
b. VT 6abc ca2 ac2 ab2 a2b bc2 b2c
VP 6abc ca2 ac2 ab2 a2b bc2 b2c VT
 Bài 5:
Cho a b c 4m . Chứng minh rằng:
 3 2 2 3 a 0
 1 a 1 a (1 a) 0 a a ,'' '' 
 a 1
 3 3 2 2 5 b 0
 1 b 1 b 1 (1 b ).b 0 b b ,'' '' 
 b 1
 2 7 c 0
Tương tự : c c ,'' '' 
 c 1
Mặt khác ta lại có : a2 b2 c2 a3 b5 c7 1 a2 a3;b2 b5;c2 c7 a,b,c
Có 1 số = 1 và 2 số = 0 A 1
 Bài 8:
Tìm các số a,b,c sao cho x3 ax2 bx c (x a)(x b)(x c)x R
 Lời giải
Ta có: (x a)(x b)(x c) (a b c)x2 (ab bc ac)x abc x3 x3 ax2 bx c
 a b c a b c 0
 b c 0,a
 ab bc ca b a(b c) bc b bc b 
 a b 1;c 1
 abc c c(1 ab) 0
 Bài 9:
Cho a,b thỏa mãn a3 3a2 5a 17 0;b3 3b2 5b 11 0. Tính A a b
 Lời giải
 3 3 2 2 3 2
(a b ) 3(a b ) 5(a b) 6 0 (a b) 3ab(a b) 3 (a b) 2ab 5(a b) 6 0
 (a b)3 3(a b)2 5(a b) 6 3ab(a b) 6ab 0
 (a b)3 3(a b)2 5(a b) 6 3ab(a b 2) 0(a b 2 a b 2 0)
 (a b)3 2(a b)2 (a b)2 2(a b) 3(a b) 6 3ab(a b 2) 0
 (a b)2 (a b 2) (a b)(a b 2) 3(a b 2) 3ab(a b 2) 0
 a b 2 0
 (a b 2)[(a+b)2 (a b) 3 3ab] 0
 2
 (a b) (a b) 3 3ab 0
 A 2
 2 2 2 2 A 2
 a ab b a b 3 0 2a 2ab 2b 
 (a b)2 (a 1)2 (b 1)2 4 0(voly)
 2a 2b 6 0
 A 2
 5 Bài 3:
Chứng minh rằng A x12 x9 x4 x 1 0x R
 Lời giải
 x9 (x3 1) 0
+) Với x 1 A 1 0x R
 3
 x(x 1) 0
 x 0
 x 0 A 0
+) Với 9 
 x 0
 1 x 0
+) Với 0 x 1 A 0
 4 9 4 5 
 x x x (1 x ) 0
Do dấu “ =” không xảy ra.
 Bài 4:
Chứng minh rằng
a. Nếu a b c 0 thì a3 b3 c3 3abc 0(a,b,c R)
b. a4 b4 c4 d 4 4abcd 0a,b,c,d R
 Lời giải
a. Có a3 b3 c3 3abc (a b c)(a2 b2 c2 ab bc ca)
mà a b c 02(gt);(a b)2 0 a2 2ab b2 0 a2 b2 2ab;a2 c2 2ac;b2 c2 2bc
 a2 b2 c2 ab bc ca a2 b2 c2 ab bc ca 0
b. a4 b4 c4 d 4 4abcd a4 b4 2a2b2 c4 d 4 2c2d 2 2a2b2 2c2d 2 4abcd
 (a2 b2 )2 (c2 d 2 )2 2(ab cd)2 a,b,c,d R
 7 a 0
 2 2 2 2 2 
Mà 1 a b c a b c 2 ab bc ca ab bc ca 0 abc 0 b 0
 c 0
 b c 1
 2 2 2 2
- Nếu a 0 b c 1 b c 2bc 1 2bc 0 a;b;c 0;0;1 hoặc 0;1;0 
 3 3
 b c 1
 0;0;1 
- Nếu b 0 a;b;c 
 1;0;0 
 0;1;0 
- Nếu b 0 a;b;c 
 1;0;0 
Vậy mọi trường hợp ta có: a2017 b2017 c2017 1
 Bài 4:
Cho biế x2 y2 z2 xy yz zx và x2017 y2017 z2017 91009. Tính giá trị của biểu thức 
 2017
 2017x 2018y 4034z 
P 2018.
 3 
 Lời giải
Ta có x2 y2 z2 xy yz zx 2x2 2y2 2z2 2xy 2yz 2zx x y 2 y z 2 z x 2 0
 1009
 x y z x2017 y2017 z2017 91009 3.x2017 32 3.x2017 32019 x 3 y z
 2017 2017
 2017x 2018y 4034z z 
Khi đó P 2018 2018 2019 .
 3 3 
 Bài 5:
 3a 2b 3b a
a) Cho a 2b 5 . Tính giá trị biểu thức A 
 2a 5 b 5
 5a b 3b 2a
b) Biết 2a b 7 . Tính B 
 3a 7 2b 7
 2a b 5b a
c) Biết 10a2 3b2 5ab 0;9a2 b2 0 . Tính C 
 3a b 3a b
 a b
d) Cho 3a2 3b2 10ab và b a 0. Tính D 
 a b
 9 Vậy M 1 với a b c 1.
 Bài 7:
 x y z 3 3 3
Tính A 1 1 1 , biết x, y, z 0; x y z 3xyz
 y z x 
 Lời giải
 x y z 0
x3 y3 z3 3xyz .... (x y z)(x2 y2 z2 xy yz zx) 0
 2 2 2
 x y z xy yz zx 0
 x y y z x z xyz
TH1: x y z 0 x y z; x z y; y z x A . . 1
 y y x xyz
TH2: x2 y2 z2 xy yz zx 0 (x y)2 (x z)2 (y z)2 0
 x y 0
 y z 0 x y z A 8
 z x 0
 BÀI TẬP TƯƠNG TỰ
 Bài 1:
 ab
Cho 4a2 b2 5ab và 2a b 0 . Tính giá trị của A 
 4a2 b2
 Hướng dẫn giải
Từ 4a2 b2 5ab 4a2 4ab ab b2 0 4a b a b 0
TH 1: 4a b 0 4a b ( mâu thẫn vì 2a > b)
 a2 1
TH 2: a b 0 a b A 
 4a2 a2 3
 Bài 2:
 3x 2y
Cho 9x2 4y2 20xy 2y 3x 0 . Tính A 
 3x 2y
 Hướng dẫn giải
Từ: 9x2 4y2 20xy x 2y 9x 2y 0
 3x x 1
TH1: x 2y A 
 3x x 2
TH2: 9x 2y (mâu thuẫn vì 2y 3x 0 )
 11