Chuyên đề Ôn thi vào lớp 10 môn Toán - Tứ giác nội tiếp

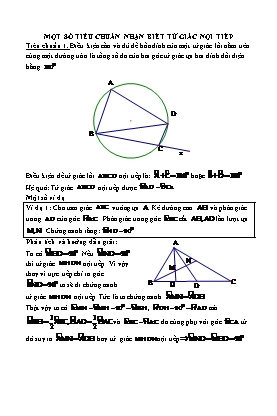
 MỘT SỐ TIÊU CHUẨN NHẬN BIẾT TỨ GIÁC NỘI TIẾP
Tiêu chuẩn 1. Điều kiện cần và đủ để bốn đỉnh của một tứ giác lồi nằm trên 
cùng một đường tròn là tổng số đo của hai góc tứ giác tại hai đỉnh đối diện 
bằng 1800 .
 A
 D
 B
 C
 x
Điều kiện để tứ giác lồi ABCD nội tiếp là: Aµ Cµ 1800 hoặc Bµ Dµ 1800
Hệ quả: Tứ giác ABCD nội tiếp được B· AD D· Cx
Một số ví dụ
Ví dụ 1: Cho tam giác ABC vuông tại A . Kẻ đường cao AH và phân giác 
trong AD của góc H· AC . Phân giác trong góc A· BC cắt AH,AD lần lượt tại 
M,N . Chứng minh rằng: B· ND 900 .
Phân tích và hướng dẫn giải: A
Ta có M· HD 900 . Nếu M· ND 900 
thì tứ giác MHDN nội tiếp. Vì vậy N
 M
thay vì trực tiếp chỉ ra góc 
· 0 C
BND 90 ta sẽ đi chứng minh B H D
tứ giác MHDN nội tiếp. Tức là ta chứng minh A· MN A· DH . 
Thật vậy ta có A· MN B· MH 900 M· BH , N· DH 900 H· AD mà 
 1 1
M· BH A· BC,H· AD H· AC và A· BC H· AC do cùng phụ với góc B· CA từ 
 2 2
đó suy ra A· MN A· DH hay tứ giác MHDN nội tiếp M· ND M· HD 900 Chú ý: Đường thẳng qua N,H,P chính là đường thẳng Steiners của điểm 
M . Thông qua bài toán này các em học sinh cần nhớ tính chất. Đường thẳng 
Steiners của tam giác thì đi qua trực tâm của tam giác đó . (Xem thêm phần 
“Các định lý hình học nổi tiếng’’).
c). Ta có M· AN 2B· AM,M· AP 2M· AC N· AP 2B· AC . Mặt khác ta có 
AM AN AP nên các điểm M,N,P thuộc đường tròn tâm A bán kính 
AM . Áp dụng định lý sin trong tam giác NAP ta có: 
NP 2R.sin N· AP 2AM.sin 2·BAC . Như vậy NP lớn nhất khi và chỉ khi 
AM lớn nhất. Hay AM là đường kính của đường tròn (O)
Ví dụ 3: Cho tam giác ABC và đường cao AH gọi M,N lần lượt là trung 
điểm của AB,AC . Đường tròn ngoại tiếp tam giác BHM cắt đường tròn 
ngoại tiếp tam giác CNH tại E . Chứng minh AMEN là tứ giác nội tiếp và 
HE đi qua trung điểm của MN . A
Phân tích, định hướng cách giải: 
Để chứng minh AMEN 
là tứ giác nội tiếp ta sẽ M I N
chứng minh: M· AN M· EN 1800 . 
Ta cần tìm sự liên hệ của các góc E
M· AN;M· EN với các góc có sẵn 
 B K C
của những tứ giác nội tiếp khác. H
 Ta có 
M· EN 3600 M· EH N· EH 3600 1800 A· BC 1800 A· CB A· BC A· CB 
 1800 B· AC suy ra M· EN M· AN 1800 . Hay tứ giác AMEN là tứ giác nội 
tiếp.
Kẻ MK  BC , giả sử HE cắt MN tại I thì IH là cát tuyến của hai đường 
tròn (BMH) , (CNH) . Lại có MB MH MA (Tính chất trung tuyến tam 
giác vuông). Suy ra tam giác MBH cân tại M KB KH MK luôn đi qua 
tâm đường tròn ngoại tiếp tam giác MBH . Hay MN là tiếp tuyến của 
(MBH) suy ra IM2 IE.IH , tương tự ta cũng có MN là tiếp tuyến của 
 HNC suy ra IN2 IE.IH do đó IM IN .
Xem thêm phần: ‘’Các tính chất của cát tuyến và tiếp tuyến’’ A,D,O cùng nằm trên đường tròn
đường kính OA .Ta mong muốn tìm 
ra được một góc bằng A· DO 900 . 
Điều này làm ta nghỉ đến tính chất
quen thuộc ‘’Đường kính đi qua trung 
điểm của một dây cung thì vuông góc
 với dây đó’’. Vì vậy nếu ta gọi M,N 
là trung điểm của AB,AC thì ta sẽ có:
 O· MA O· NA 900 . Do đó tứ giác OMAN nội tiếp. Công việc còn lại là ta 
chứng minh AMDO hoặc ANOD hoặc DMAN là tứ giác nội tiếp. Mặt 
khác ta có: A· BD C· AD và A· CD B· AD (Tính chất góc tạo bởi tiếp tuyến và 
dây cung) BDA và ADC đồng dạng nên ta suy ra D· MA D· NC 
 D· MA D· NA D· NC D· NA 1800 AMDN nội tiếp suy ra năm điểm 
A,M,D,O,N nằm trên đường tròn đường kính OA A· DO 900
Ví dụ 6: Cho tam giác ABC vuông cân tại A một đường tròn O tiếp xúc 
với AB,AC tại B,C . Trên cung B»C nằm trong tam giác ABC lấy một điểm 
M M B;C . Gọi I,H,K lần lượt là hình chiếu của M trên BC;CA; AB và 
P là giao điểm của MB với IK, Q là giao điểm của MC với IH . Chứng 
minh PQ / /BC .
Phân tích định hướng giải: A
Để chứng minh PQ / /BC 
 H
ta chứng minh M· PQ M· BC 
 K M
nhưng tứ giác BIMK nội tiếp
 Q
 nên M· BC M· KI . Mặt khác P
 B C
AC là tiếp tuyến của (O) nên I
 · ·
ta có: ACK MBC và CIMH O
nội tiếp nên A· CK M· IH .Như vậy để chứng minh PQ / /BC ta cần chứng 
minh M· IH M· PQ . Tức là ta cần chứng minh tứ giác MPIQ nội tiếp . Để ý 
rằng B· MC K· MH 1350 , P· IQ P· IM I·MQ 
 1
 K· BM K· CH sđ B¼M M¼ C 450 suy ra đpcm.(Các em học sinh tự 
 2 
hoàn thiện lời giải) Kẻ đường kính AM cắt d tại N . Ta có A· NE A· BE 900 nên tứ giác 
ABNE nội tiếp, suy ra B· EN B· AN .
 A
Mặt khác B· AN B· CM , 
do đó B· CM B· EN hay B· CD B· ED .
Vậy B,C,D,E cùng thuộc một đường tròn.
 O
 C
 B
 M
 E
 N
 D
Ví dụ 3) Cho tam giác ABC có các đường cao AD,BE,CF đồng quy tại H . 
Gọi K là giao điểm của EF và AH , M là trung điểm của AH . Chứng 
minh rằng K là trực tâm của tam giác MBC . A
Lời giải:
Lấy điểm S đối xứng với H qua 
 M E
BC , R là giao điểm của KC với MB . R
Vì ME MA MH (Tính chất trung F K
 tuyến), kết hợp tính đối xứng của điểm H
S ta có M· SB B· HD M· HE M· EB 
 B C
nên tứ giác MESB nội tiếp. Suy ra D
 R· BE M· SE (1).
Lại có K· SC C· HD A· HF A· EK nên tứ giác KSCE cũngS nội tiếp, do đó 
M· SE R· CE (2).Từ (1) và (2) suy ra R· BE R· CE nên tứ giác RBCE nội tiếp. 
Từ đó suy ra B· RC B· EC 900 . Trong tam giác MBC , ta có MK  BC và 
CK  MB nên K là trực tâm của tam giác MBC .
Ví dụ 4) Cho tam giác ABC nội tiếp đường tròn tâm O . Đường tròn (O') 
tiếp xúc với các cạnh AB,AC tại E,F tiếp xúc với (O) tại S . Gọi I là tâm 
đường tròn nội tiếp tam giác ABC .Chứng minh BEIS,CFIS là các tứ giác 
nội tiếp. 
Lời giải: A
 M
 N
 O
 I E
 F
 O'
 C B
 S x là góc nội tiếp chắn nữa đường 
tròn. Vì vậy để chứng minh AE  MH 
ta phải chứng minh AD2  ME , tức là 
ta chứng minh H là trực tâm của tam 
giác MAE . Khi đó ta sẽ có:
· ·
 AD1E AD2E 
hay tứ giác AD1D2E là tứ giác nội tiếp. 
+ Gọi N là giao điểm của CD2 và AM .
 Xét tiếp tuyến chung của (O1) và (O2 ) qua B cắt ( ) tại I . Khi đó ta có: 
ID1 IB ID2 BD1D2 vuông tại B , D1E / /CN (cùng vuông góc với BD2
 · ·
). Do đó BAD1 BD1D2 (Góc tạo bởi tia tiếp tuyến và dây cung), mặt khác 
· · · ·
BD1D2 D1D2N (so le trong). Suy ra CAD1 ND2D1 AD1D2C là tứ giác 
nội tiếp. (1) Xét tứ giác ED1D2C ta có: 
 · · · ·
ED1 / /CD2 ,BEC IBD1 ( góc đồng vị). Suy ra ED1D2 D1EC suy ra tứ giác 
ED1D2C là hình thang cân nên nội tiếp được (2). Từ (1), (2) ta suy ra 5 
điểm A,D1 ,D2 ,C,E cùng thuộc một đường tròn. Suy ra tứ giác AD1D2E nội 
tiếp được.
Ví dụ 6) Cho tam giác ABC có hai đường cao BD,CE cắt nhau tại H gọi I 
là trung điểm của BC . Hai đường tròn ngoại tiếp tam giác BEI và CDI cắt 
nhau ở K , DE cắt BC tại M . Chứng minh tứ giác BKDM nội tiếp.
Phân tích định hướng giải:
Ta thấy ngay đường tròn ngoại tiếp các tam giác ADE,BEI,CDI sẽ cắt nhau 
tại điểm K (Định lý Miquel). Như vậy ta sẽ thấy AEKD là tứ giác nội tiếp, 
mặt khác từ giả thiết ta cũng có: AEHD là tứ giác nội tiếp. Nên suy ra 5 
điểm A,E,H,K,D thuộc một đường tròn đường kính AH . Đây chính là chìa 
khóa để giải quyết bài toán .
Lời giải: Trước tiên ta chứng minh: tứ giác AEKD nội tiếp (Bạn đọc có thể 
tham khảo ở phần ‘’Các định lý hình họcA nổi tiếng’’) Ta có: 
Aµ Bµ Cµ E· KC E· KI I·KD 5400. Theo giả thiết Bµ E· KI I·KD Cµ 1800
 Aµ E· KD 1800 tứ giác AEKD nội tiếp A· DE A· KE , 
BD  AC,CE  AB tứ giác BEDC nội tiếp A· DDE Bµ . Kết hợp với 
 E
 K
 H
 M C
 B I FA EA
ME,MF . Ta có tính chất quen thuộc: (Xem phần chùm bài tập cát 
 FB EB
 FB FA
tuyến và tiếp tuyến). Từ đó suy ra thay vào (*) ta quy bài toán về 
 EB EA
 EP FA EP EA
chứng minh: . 1 EPA : FQA nhưng ta có: 
 FQ EA FQ FA
E· PA F· QA góc nội tiếp chắn cung AB . A· EP A· FQ (tứ giác AEBF nội 
tiếp) . Qua đó ta có kết quả cần chứng minh:
Các em học sinh tự hoàn chỉnh lời giải dựa trên những phân tích định hướng 
mà tác giải vừa trình bày.
Nếu không dùng định lý Menaleuyt ta có thể giải theo các khác như 
sau:
 · ·
Vì MF là tiếp tuyến của đường tròn (O1) nên ta có: MFB FAB (Tính chất 
góc tạo bởi tiếp tuyến và dây cung). Suy ra MFB, MAF đồng dạng 
 MF FB
 . Tương tự ta cũng có: MEB, MAE đồng dạng suy ra 
 MA FA
 ME EB FB EB
 , mà ME MF (1) , mặt khác A· FE A· BE (chắn 
 MA EA FA EA
cung AE ) và A· BE A· QP (do tứ giác ABPQ nội tiếp). Suy ra 
A· FE A· QP AFIQ là tứ giác nội tiếp, suy ra A· FQ A· IQ A· FB A· IP , ta 
 BF PI
cũng có: A· BF A· PQ suy ra FBA, IPA đồng dạng suy ra (2). 
 AF AI
 QI BE
Tương tự ta chứng minh được: ABE, AQI đồng dạng suy ra 
 IA AE
 QI PI
(3).Từ (1), (2), (3) suy ra IP IQ
 IA IA
Ví dụ 8) Cho tam giác ABC . Đường tròn O đi qua A và C cắt AB,AC 
theo thứ tự tại K và N . Đường tròn tâm I ngoại tiếp tam giác ABC và 
đường tròn tâm J ngoại tiếp tam giác KBN cắt nhau tại B và M . Chứng 
minh BIOJ là hình bình hành từ đó suy ra O· MB vuông.
Phân tích định hướng giải:
 x B
Để chứng minh BIOJ là 
hình bình hành ta chứng minh M
BI / /OJ,BJ / /OI . J N
 Q
 K I
 O
 A C