Chuyên đề Ôn thi vào lớp 10 môn Toán - Tiếp tuyến, cát tuyến

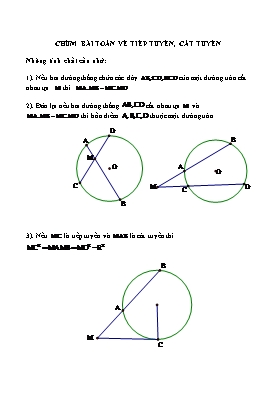
 CHÙM BÀI TOÁN VỀ TIẾP TUYẾN, CÁT TUYẾN
Những tính chất cần nhớ: 
1). Nếu hai đường thẳng chứa các dây AB,CD,KCD của một đường tròn cắt 
nhau tại M thì MA.MB MC.MD
2). Đảo lại nếu hai đường thẳng AB,CD cắt nhau tại M và 
MA.MB MC.MD thì bốn điểm A,B,C,D thuộc một đường tròn.
 D
 A B
 M
 O A
 O
 C
 M C D
 B
3). Nếu MC là tiếp tuyến và MAB là cát tuyến thì 
MC2 MA.MB MO2 R2
 B
 A
 M
 C BC KC AC BC
Tương tự ta cũng có: mà KA KB nên suy ra 
 BD KB AD BD
 AC BC
Chú ý: Những tứ giác quen thuộc ACBD như trên thì ta luôn có: 
 AD BD
 CA DA
và 
 CB DB
 NHỮNG BÀI TOÁN TIÊU BIỂU
Bài 1: Từ điểm K nằm ngoài đường tròn ta kẻ các tiếp tuyến KA,KB cát 
tuyến KCD đến (O) . Gọi M là giao điểm OK và AB . Vẽ dây DI qua M . 
Chứng minh
 a) KIOD là tứ giác nội tiếp 
 b) KO là phân giác của góc IKD
Giải:
 A
 D
 C
 M
 K O
 I
 B
 a) Để chứng minh KIOD là tứ giác nội tiếp việc chỉ ra các góc là rất 
 khó khăn.
Ta phải dựa vào các tính chất của cát tuyến , tiếp tuyến.
Ta có: AIBD là tứ giác nội tiếp và AB  ID M nên ta có: MA.MB MI.MD
Mặt khác KAOB là tứ giác nội tiếp nên MA.MB MO.MK Tia KD thuộc nửa mặt phẳng chứa A và bờ là KO (h1)
Hai góc A· MC,A· MD có 2 góc phụ với nó tương ứng là K· MC,O· DC mà 
K· MC O· DC nên A· MC A· MD hay MA là tia phân giác của góc C· MD
Trường hợp 2:
Tia KD thuộc nửa mặt phẳng chứa B và bờ là KO (h2) thì tương tự ta cũng 
có MB là tia phân giác của góc C· MD
Suy ra Đường thẳng AB chứa phân giác của góc C· MD .
Bài 3. Từ điểm K nằm ngoài đường tròn ta (O) kẻ các tiếp tuyến KA,KB 
cát tuyến KCD đến (O) . Gọi H là trung điểm CD . Vẽ dây AF đi qua H . 
Chứng minh BF / /CD
Giải:
 A D
 H
 C
 K O
 F
 B
Để chứng minh BF / /CD ta chứng minh A· HK A· FB
 1
Ta có A· FB A· OB ( Tính chất góc nội tiếp chắn cung AB ).
 2 (O) tại A cắt IB ở K . Gọi C là giao điểm thứ hai của KD với đường tròn 
(O) . Chứng minh rằng BC / /AI .
Giải:
 K
 C B
 O
 A
 D I
Ta cần chứng minh: A· IK K· BC
 1
Mặt khác ta có: K· BC C· AB sđC»B nên ta sẽ chứng minh A· IK C· AB hay 
 2
 CB DB
 BID : BCA Thật vậy theo tính chất 5 ta có: mà 
 CA DA
 CB DB
DA DI 
 CA DI
Tứ giác ACBD nội tiếp nên B· CA B· DI BID : BCA A· IK C· AB
Hay A· IK K· BC BC / /AI
Bài 6 Từ điểm K nằm ngoài đường tròn ta (O) kẻ các tiếp tuyến KA,KB Giải:
 E
 a) Theo bài toán 2, ta có CMOD
 D
là tứ giác nội tiếp nên C· MK O· DC O· CD . A
 H
 C
Do đó các góc phụ với chúng 
 K
 M O
bằng nhau: C· ME C· OE .
Suy ra CMOE là tứ giác nội tiếp (theo cung chứa góc). B
 c) Cũng theo bài toán 2, CMOD nội tiếp. 
Mặt khác CMOE là tứ giác nội tiếp nên E,C,M,O,D thuộc một đường tròn.
Từ đó dễ chứng minh CE,DE là tiếp tuyến của đường tròn (O)
Bài 8) Từ điểm K nằm ngoài đường tròn ta (O) kẻ các tiếp tuyến KA,KB 
cát tuyến KCD đến (O) . Vẽ đường kính AI . Các dây IC,ID cắt KO theo 
thứ tự ở G,N . Chứng minh rằng OG ON .
Giải:
 A
 1 D
 C
 1
 K
 G M O N
 1
 I Kẻ OH  CD , cắt AB ở E .
Theo bài 7 , EC là tiếp tuyến của đường tròn O , nên theo bài toán quen 
thuộc 3, ta có ECMD là tứ giác nội tiếp, suy ra E· BD E· CD (2).
Từ (1) và (2) suy ra C· BD E· MD .
Do đó hai góc bù với nhau chúng bằng nhau: C· AD B· MD 
 · ·
 CAD : BMD (g.g) nên ADC MDB