Chuyên đề Ôn thi TN THPT - Chuyên đề 14: Mũ, logarit

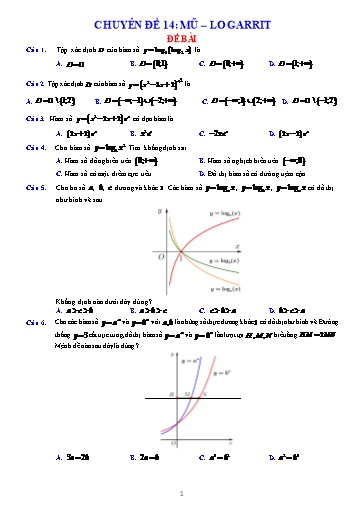
 CHUYÊN ĐỀ 14: MŨ – LOGARRIT 
 ĐỀ BÀI
Câu 1. Tập xác định D của hàm số y log3 log2 x là
 A. D ¡ . B. D 0;1 . C. D 0; . D. D 1; .
 2
Câu 2. Tập xác định D của hàm số y x2 3x 2 là 
A. D ¡ \ 1;2. B. D ; 1  2; . C. D ;1  2; . D. D ¡ \ 1;2
Câu 3. Hàm số y x2 2x 2 ex có đạo hàm là
 A. 2x 2 ex . B. x2ex . C. 2xex . D. 2x 2 ex .
 2
Câu 4. Cho hàm số y log2 x . Tìm khẳng định sai.
 A. Hàm số đồng biến trên 0; . B. Hàm số nghịch biến trên ;0 .
 C. Hàm số có một điểm cực tiểu. D. Đồ thị hàm số có đường tiệm cận.
Câu 5. Cho ba số a , b , c dương và khác 1. Các hàm số y loga x , y logb x , y logc x có đồ thị 
 như hình vẽ sau
 Khẳng định nào dưới đây đúng?
 A. a c b . B. a b c . C. c b a . D. b c a .
Câu 6. Cho các hàm số y a x và y bx với a,b là những số thực dương khác 1 có đồ thị như hình vẽ. Đường 
 x x
 thẳng y 3 cắt trục tung, đồ thị hàm số y a và y b lần lượt tại H, M , N biết rằng HM 2MN . 
 Mệnh đề nào sau đây là đúng ?
 A. 3a 2b . B. 2a b . C. a3 b2 . D. a2 b3 .
 1 2a b a
Câu 15. Cho các số thực dương a , b thỏa mãn log a log b log . Tính tỉ số T .
 16 20 25 3 b
 1 1 2
 A. 0 T . B. T . C. 2 T 0 . D. 1 T 2 .
 2 2 3
 40
Câu 16. Cho a log 5 , b log 9. Biểu diễn của P log theo a và b là:
 2 2 2 3
 1 3a
 A. P 3 a 2b . B. P 3 a b . C. P . D. P 3 a b .
 2 2b
 xab ya zb 1
Câu 17. Cho a log 5,b log 3 , log 150 x, y, z,m,n, p,q ¢ . 
 2 5 30 mab na pb q
 Tổng S x y z m n p q bằng
 A. S 5. B. S 4 . C. S 6 . D. S 1.
 x x
Câu 18. Gọi x1, x2 là hai nghiệm của phương trình 9 4.3 3 0 . Tính tổng S x1 x2 . 
 A. S 1. B. S 4 . C. S 9 . D. S 10 .
Câu 19. Tìm nghiệm của phương trình 2x 1 2x 1 2x 28 .
 1
 A. x 2 . B. x 3. C. x . D. x 16 .
 3
 3
 x2 x 
 2
Câu 20. Gọi x1, x2 là hai nghiệm thực phân biệt của phương trình 7 49 7 . 
 Tính giá trị biểu thức P x1.x2 .
 A. P 1. B. P 0 . C. P 1. D. P 4 .
Câu 21. Nghiệm của phương trình log x log x log x 6 là 
 3 3 1
 3
 A. x 312 . B. x 3 3 . C. x 27 . D. x 9 .
 x 1
 x x
Câu 22. Gọi các nghiệm của phương trình 5 .8 500 là x a và x logb 2 với a 0 , 0 b,c 1. 
 Tổng a b là
 A. 8 . B. 9 . C. 10. D. 11 .
 a b
Câu 23. Cho hai số thực dương a b thỏa mãn log a log b log 5a 12b . Tính P .
 20 8 125 b
 A. P 3. B. P 4 . C. P 2 . D. P 8 .
 2
Câu 24. Gọi x1 x2 là các nghiệm của phương trình log5 x 4log5 x 2 0 . Tính x1.x2 
 A. x1.x2 2 . B. x1.x2 4 . C. x1.x2 625 . D. 
 x1.x2 32 .
Câu 25. Tổng tất cả các nghiệm của phương trình 32 x 2.3x 2 27 0 bằng 
 A. 18. B. 27. C. 9. D. 3.
 2 3
Câu 26. Tìm tất cả các giá trị thực của tham số a để phương trình log3 x a log3 x a 1 0 có 
 nghiệm duy nhất. 
 A. a 1. B. a 1. C. a 1. D. a 1.
 1 2 1 1
Câu 27. Phương trình 1 có hai nghiệm x1,x2 thì là 
 5 log2 x 1 log2 x x1 x2
 3 33
 A. B. . C. 5. D. 66.
 8 64
 3 3x 7 
Câu 41. Bất phương trình log2 log1 0 có tập nghiệm là a;b . Tính giá trị P 6a b . 
 3 x 3 
 A. P 12 . B. P 11. C. P 10 . D. P 9 .
Câu 42. Biết S a;b là tập nghiệm của bất phương trình 3.9x 10.3x 3 0 . Tìm T 2a2 3b 6 .
 A. T 2 . B. T 1. C. T 2 . D. T 1.
 1
 x 
Câu 43. Tìm tập nghiệm S của bất phương trình 4 2 20.2x 32 0 là.
 A . S ;1  3; .B . S 1;3 .
 C . S 1;4 .D . S ;1  4; .
 2
 3
Câu 44. Tìm tất cả các giá trị thực của tham số m để bất phương trình 9 log3 x log3 x 2m 0 
 nghiệm đúng với mọi giá trị x 3;81 .
 A. m 1. B. m 10 . C. m 10 . D. m 1.
Câu 45. Tìm giá trị gần đúng tổng các nghiệm của bất phương trình sau:
 22 22 2 4 
 2log2 2log 5 13 4 24x6 2x5 27x4 2x3 1997x2 2019 0
 x x 2 
 3 3 log x log x
 22 22 
 3 3 
 A. 12,3 . B. 12. C. 12,1. D. 12,2 .
Câu 46. Số nghiệm nguyên của bất phương trình log2 x log3 x 1 log2 x.log3 x là
 A. 1. B. 2 . C. 3 . D. Vô số.
 2
Câu 47. Bất phương trình 2x x 2.3x 3 9.41 x có tập nghiệm 
 S ;log2 alog2 b; . Tính a b 
 1 5
 A. 5 . B. . C. . D. 5 .
 6 6
 2
 2x 1 1 
Câu 48. Bất phương trình log4 x 2 x 3 log2 1 2 x 2 có tập nghiệm là 
 x x 
 S a;b  c;d . Tính a b c d
 13 2 13 3 3 13
 A. . B. . C. . D. 2 .
 2 2 2
Câu 49. Cho phương trình m 3 9log2 x 2 m 1 xlog2 3 m 1 0 1 . Biết rằng tập các giá trị của tham 
 số m để phương trình có hai nghiệm phân biệt là một khoảng a;b . Tổng S a b bằng 
 A. 4 . B. 6 . C. 8 . D. 10.
Câu 50. Gọi S là tập tất cả các giá trị nguyên của m để phương trình 
 2 2 2 2 2
 5x 4x 3 5x 2mx 2m 6m 1 25x m 2 x m 3m 1 1 có bốn nghiệm phân biệt. Số phần tử của tập S là
 A. 1. B. 3 . C. 4 . D. 5.
 5 (x2 ) 2x 2
 Đạo hàm: y .
 x2 ln 2 x2 ln 2 xln 2
 Bảng biến thiên:
 Từ bảng biên thiên ta thấy hàm số đồng biến trên 0; và nghịch biến trên ;0 ; Đồ thị 
 hàm số có tiệm cận đứng là đường thẳng x 0 và không có điểm cực trị. Do đó khẳng định ở 
 đáp án C là sai. 
nguyenhotu@gmail.com
Câu 5. Cho ba số a , b , c dương và khác 1. Các hàm số y loga x , y logb x , y logc x có đồ thị 
 như hình vẽ sau
 Khẳng định nào dưới đây đúng?
 A. a c b . B. a b c . C. c b a . D. b c a .
 Lời giải
 Chọn A
 Dựa vào đồ thị ta thấy:
 Hàm số y loga x đồng biến trên tập xác định nên a 1.
 Hàm số y logb x và y logc x nghịch biến trên tập xác định nên 0 b 1, 0 c 1.
 Suy ra a b và a c .
 Mặt khác, với x 1 ta có logb x logc x b c . Vậy a c b .
 Phương pháp trắc nghiệm:
 7