Chuyên đề Ôn thi THPTQG - Chuyên đề 8: Tương giao đồ thị hàm số (Mức 9-10 điểm) - Phần 2

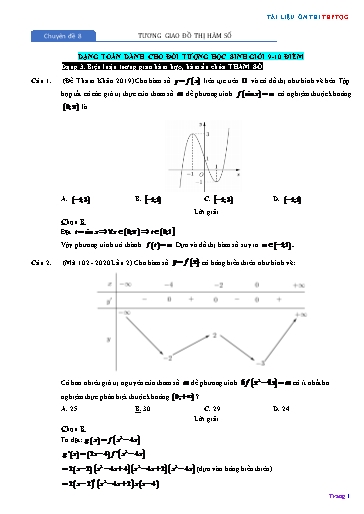
 TÀI LIỆU ÔN THI THPTQG
 Chuyên đề 8 TƯƠNG GIAO ĐỒ THỊ HÀM SỐ
 DẠNG TOÁN DÀNH CHO ĐỐI TƯỢNG HỌC SINH GIỎI 9-10 ĐIỂM
 Dạng 3. Biện luận tương giao hàm hợp, hàm ẩn chứa THAM SỐ
Câu 1. (Đề Tham Khảo 2019) Cho hàm số y f x liên tục trên ¡ và có đồ thị như hình vẽ bên. Tập 
 hợp tất cả các giá trị thực của tham số m để phương trình f sin x m có nghiệm thuộc khoảng 
 0; là
 A. 1;3 B.  1;1 C.  1;3 D. 1;1 
 Lời giải
 Chọn B
 Đặt t sin x x 0; t 0;1
 Vậy phương trình trở thành f t m . Dựa và đồ thị hàm số suy ra m  1;1 .
Câu 2. (Mã 102 - 2020 Lần 2) Cho hàm số y f x có bảng biến thiên như hình vẽ:
 Có bao nhiêu giá trị nguyên của tham số m để phương trình 6 f x2 4x m có ít nhất ba 
 nghiệm thực phân biệt thuộc khoảng 0; ?
 A. 25. B. 30. C. 29. D. 24.
 Lời giải
 Chọn B
 Ta đặt: g x f x2 4x .
 g x 2x 4 f x2 4x 
 2 x 2 x2 4x 4 x2 4x 2 x2 4x (dựa vào bảng biến thiên)
 2 x 2 3 x2 4x 2 x x 4 .
 Trang 1 TÀI LIỆU ÔN THI THPTQG
 + Với u 4 , phương trình (1) vô nghiệm.
 + Với u 4, phương trình (1) có một nghiệm x 2 0 .
 + Với 4 u 0 , phương trình (1) có hai nghiệm x 0 .
 + Vơi u 0 , phương trình (1) có một nghiệm x 0
 m
 Khi đó 3 f x2 4x m f u (2), ta thấy:
 3
 m
 + Nếu 3 m 9 , phương trình (2) có một nghiệm u 0 nên phương trình đã cho có một 
 3
 nghiệm x 0 .
 m
 + Nếu 3 2 9 m 6 , phương trình (2) có một nghiệm u 0 và một nghiệm 
 3
 u 2;0 nên phương trình đã cho có ba ngiệm x 0 .
 m
 + Nếu 2 m 6 , phương trình (2) có một nghiệm u 4, một nghiệm u 2;0 và 
 3
 một nghiệm u 0 nên phương trình đã cho có bốn nghiệm x 0 .
 m
 + Nếu 2 2 6 m 6 , phương trình (2) có một nghiệm u 4 , hai nghiệm u 4;0 
 3
 và một nghiệm u 0 nên phương trình đã cho có năm nghiệm x 0 .
 m
 + Nếu 2 m 6 , phương trình (2) có một nghiệm u 4 , một nghiệm u 2 và một 
 3
 nghiệm u 0 nên phương trình đã cho có ba nghiệm x 0 .
 m
 + Nếu 2 m 6 , phương trình (2) có một nghiệm u 4 và một nghiệm u 0 nên 
 3
 phương trình đã cho có một nghiệm x 0 .
 Vậy 9 m 6 có 15 giá trị m nguyên thỏa ycbt.
Câu 4. (Mã 101 – 2020 Lần 2) Cho hàm số f x có bảng biến thiên như sau:
 Có bao nhiêu giá trị nguyên của tham số m để phương trình 5 f x2 4x m có ít nhất 3 nghiệm 
 phân biệt thuộc khoảng 0; 
 A. 24 . B. 21. C. 25 . D. 20 .
 Lời giải
 ChọnC.
 Đặt t x2 4x . Ta có t 2x 4 0 x 2
 Bảng biến thiên
 Trang 3 TÀI LIỆU ÔN THI THPTQG
Câu 6. (Chuyên Biên Hòa - Hà Nam - 2020) Cho hàm số f x . Hàm số y f x có đồ thị như hình 
 sau.
 Tìm tất cả các giá trị thực của tham số m để bất phương trình 
 2sin3 x 5cos 2x 
 2 f sin x 2 sin x m nghiệm đúng với mọi x ; .
 3 4 2 2 
 11 19
 A. m 2 f 3 . B. m 2 f 1 .
 12 12
 19 11
 C. m 2 f 1 . D. m 2 f 3 .
 12 12
 Lời giải
 Chọn C
 Ta có
 2sin3 x 5cos 2x
 2 f sin x 2 sin x m 
 3 4
 2
 2sin3 x 5 1 2sin x 
 m 2 f sin x 2 sin x 
 3 4
 Đặt t sin x 2 (với x ; thì t 3; 1 , khi đó bất phương trình được viết lại thành:
 2 2 
 2
 2 t 2 3 5 1 2 t 2 
 m 2 f t t 2 .
 3 4
 2 3 65
 hay m 2 f t t3 t 2 3t * .
 3 2 12
 2 3 65
 Xét hàm số g t 2 f t t3 t 2 3t trên đoạn  3; 1 .
 3 2 12
 3 3
 Ta có g t 2 f t 2t 2 3t 3. Do đó g t 0 f t t 2 t .
 2 2
 Trang 5 TÀI LIỆU ÔN THI THPTQG
 f (x) 2 0 f (x) 2 1 
 f (x) 2 m 0 f (x) m 2 2 
 Dựa vào đồ thị hàm số y f (x) ax3 bx2 cx d ta có đồ thị hàm số y f (x) như sau:
 Dựa vào đồ thị hàm số y f (x) suy ra phương trình 1 có 4 nghiệm phân biệt.
 Suy ra phương trình đã cho có 6 nghiệm phân biệt 2 có 2 nghiệm phân biệt khác các nghiệm 
 của phương trình 1 .
 Ta có phương trình 2 là phương trình hoành độ giao điểm của hai đường y f (x) và 
 y m 2 . Số nghiệm phương trình 2 là số giao điểm của 2 đồ thị hàm số y f (x) và 
 y m 2 . Dựa vào hình vẽ đồ thị hàm số y f (x) ta được phương trình f (x) m 2 có 2 
 m 2 0
 m 2
 nghiệm phân biệt khác các nghiệm của phương trình f (x) 2 m 2 4 
 m 2
 m 2 2
 Do m ¢ và m 5;5 m 2;3;4 .
 Vậy có 3 giá trị nguyên m 5;5 thỏa mãn điều kiện bài toán.
Câu 8. (Chuyên Lam Sơn - 2020) Cho hàm số y f x , hàm số y f x liên tục trên ¡ và có đồ 
 thị như hình vẽ bên. Bất phương trình f x x2 2x m (m là tham số thực) nghiệm đúng với 
 mọi x 1;2 khi và chỉ khi
 A. m f 2 2 . B. m f 1 1. C. m f 1 1. D. m f 2 .
 Lời giải
 Chọn D
 Trang 7 TÀI LIỆU ÔN THI THPTQG
 3m min f x 
  1;4
 với mọi x thuộc đoạn  1;4 .
 m max f x 
  1;4
 Từ đồ thị hàm số y f x ta suy ra min f x 2; max f x 3 .
  1;4  1;4
 3m min f x 2
  1;4 3m 2 m 
 3 m 3 (thỏa mãn điều kiện m 0 )
 m max f x m 3 
  1;4 m 3
 Vậy trên đoạn  10;10 có 7 giá trị nguyên của m thỏa mãn điều kiện bài toán.
Câu 10. (Chuyên Bến Tre - 2020) Cho hàm số y f x . Đồ thị hàm số y f ' x như hình vẽ. Cho bất 
 phương trình 3f x x 3 3x m (m là tham số thực). Điều kiện cần và đủ để bất phương trình 
 3f x x 3 3x m đúng với mọi x 3; 3 là
 y
 2
 - 3 O 3 x
 -1
 A. m 3 f 1 . B. m 3 f 3 . C. m 3f 0 . D. m 3 f 3 .
 Lời giải
 Chọn D
 Ta có 3f x x 3 3x m 3f x x 3 3x m
 Đặt g x 3 f x x3 3x . Tính g ' x 3 f ' x 3x2 3
 Có g ' x 0 f ' x x2 1
 Nghiệm của phương trình g ' x 0 là hoành độ giao điểm của đồ thị hàm số y f ' x và 
 parabol y x2 1
 y
 2
 - 3 O 3 x
 -1
 x 3
 2 
 Dựa vào đồ thị hàm số ta có: f ' x x 1 x 0
 x 3
 BBT
 Trang 9