Chuyên đề Ôn thi THPTQG - Chuyên đề 34: Tập hợp điểm số phức

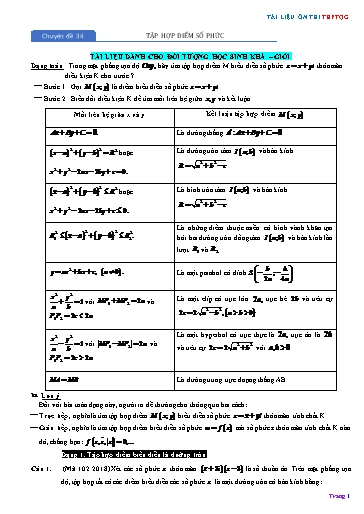
 TÀI LIỆU ÔN THI THPTQG
 Chuyên đề 34 TẬP HỢP ĐIỂM SỐ PHỨC
 TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ – GIỎI
Dạng toán. Trong mặt phẳng tọa độ Oxy, hãy tìm tập hợp điểm M biểu diễn số phức z x yi thỏa mãn 
 điều kiện K cho trước ? 
  Bước 1. Gọi M x; y là điểm biểu diễn số phức z x yi .
  Bước 2. Biến đổi điều kiện K để tìm mối liên hệ giữa x, y và kết luận.
 Mối liên hệ giữa x và y Kết luận tập hợp điểm M x; y 
 Ax By C 0. Là đường thẳng d : Ax By C 0 .
 2 2
 x a y b R2 hoặc Là đường tròn tâm I a;b và bán kính 
 R a2 b2 c .
 x2 y2 2ax 2by c 0.
 2 2
 x a y b R2 hoặc Là hình tròn tâm I a;b và bán kính 
 R a2 b2 c .
 x2 y2 2ax 2by c 0.
 Là những điểm thuộc miền có hình vành khăn tạo 
 R2 x a 2 y b 2 R2.
 1 2 bởi hai đường tròn đồng tâm I a;b và bán kính lần 
 lượt R1 và R2 .
 2 b 
 y ax bx c, a 0 . Là một parabol có đỉnh S ; .
 2a 4a 
 x2 y2
 1 với MF MF 2a và Là một elíp có trục lớn 2a, trục bé 2b và tiêu cự 
 a b 1 2
 2c 2 a2 b2 , a b 0 .
 F1F2 2c 2a .
 Là một hyperbol có trục thực là 2a, trục ảo là 2b 
 x2 y2
 1 với MF MF 2a và 2 2
 a b 1 2 và tiêu cự 2c 2 a b với a,b 0 .
 F1F2 2c 2a .
 MA MB . Là đường trung trực đoạng thẳng AB.
 Lưu ý
 Đối với bài toán dạng này, người ra đề thường cho thông qua hai cách:
 Trực tiếp, nghĩa là tìm tập hợp điểm M x; y biểu diễn số phức z x yi thỏa mãn tính chất K.
 Gián tiếp, nghĩa là tìm tập hợp điểm biểu diễn số phức w f z mà số phức z thỏa mãn tính chất K nào 
 đó, chẳng hạn: f z, z, z 0,...
 Dạng 1. Tập hợp điểm biểu diễn là đường tròn
Câu 1. (Mã 102 2018) Xét các số phức z thỏa mãn z 3i z 3 là số thuần ảo. Trên mặt phẳng tọa 
 độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng:
 Trang 1 TÀI LIỆU ÔN THI THPTQG
 Ta có: z 2i z 2 a bi 2i a bi 2 a2 2a b2 2b 2 a b 2 i
 2 2
 Vì z 2i z 2 là số thuần ảo nên ta có a2 2a b2 2b 0 a 1 b 1 2 .
 Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán 
 kính bằng 2 .
Câu 5. (Đề Minh Họa 2017) Cho các số phức z thỏa mãn z 4. Biết rằng tập hợp các điểm biểu diễn 
 các số phức w (3 4i)z i là một đường tròn. Tính bán kính r của đường tròn đó
 A. r 22 B. r 4 C. r 5 D. r 20
 Lời giải
 Chọn D
 Giả sử z a bi;w x yi; a,b, x, y ¡ 
 Theo đề w 3 4i z i x yi 3 4i a bi i
 x 3a 4b x 3a 4b
 x yi 3a 4b 3b 4a 1 i Ta có 
 y 3b 4a 1 y 1 3b 4a
 x2 y 1 2 3a 4b 2 4a 3b 2 25a2 25b2 25 a2 b2 
 Mà z 4 a2 b2 16. Vậy x2 y 1 2 25.16 400
 Bán kính đường tròn là r 400 20 .
Câu 6. (Đề Tham Khảo 2019) Xét các số phức z thỏa mãn z 2i z 2 là số thuần ảo. Biết rằng tập 
 hợp tất cả các điểm biểu diễn của z là một đường tròn, tâm của đường tròn đó có tọa độ là
 A. 1;1 B. 1;1 C. 1; 1 D. 1; 1 
 Lời giải
 Chọn C
 Gọi z x yi z x yi
 z 2i z 2 
 z.z 2z 2iz 4i
 x2 y2 2 x yi 2i x yi 4i
 x2 y2 2x 2y 2x 2y 4 i
 z 2i z 2 là số thuần ảo x2 y2 2x 2y 0
 Vậy tập hợp các điểm biểu diễn của z là một đường tròn có tâm là I 1; 1 .
Câu 7. (Mã 101 2018) Xét các số phức z thỏa mãn z i z 2 là số thuần ảo. Trên mặt phẳng tọa độ, 
 tập hợp tất cả các điểm biểu diễn số phức z là một đường tròn có bán kính bằng
 3 5 5
 A. B. 1 C. D. 
 2 4 2
 Lời giải
 Chọn D
 Đặt z x yi x, y ¡ .
 Trang 3 TÀI LIỆU ÔN THI THPTQG
Câu 10. (Mã 103 - 2019) Xét các số phức z thỏa mãn z 2 . Trên mặt phẳng tọa độ Oxy , tập hợp các 
 2 iz
 điểm biểu diễn số phức w là một đường tròn có bán kính bằng
 1 z
 A. 10 . B. 2 . C. 2 . D. 10.
 Lời giải
 Chọn A
 Gọi số phức w x yi; x, y ¡ . Khi đó:
 2 iz
 w w 1 z 2 iz w 2 z i w w 2 z i w w 2 z  z i w 
 1 z
 x 2 2 y2 2 x2 1 y 2 x 2 2 y 2 2 10 * 
 Từ * suy ra điểm biểu diễn số phức w là một đường tròn có bán kính bằng 10 .
Câu 11. (THPT Gia Lộc Hải Dương -2019) Cho số phức z thỏa mãn z 2. Biết rằng tập hợp các 
 điểm biểu diễn số phức w 3 2i 2 i z là một đường tròn. Tìm tọa độ tâm I của đường tròn 
 đó?
 A. I 3; 2 . B. I 3;2 . C. I 3;2 . D. I 3; 2 .
 Lời giải
 Cách 1.
 Đặt w x yi .Ta có w 3 2i 2 i z .
 x yi 3 2i 2 i z .
 2 i z x 3 y 2 i .
 2
 4 i z x 3 y 2 i . 2 i .
 2x y 8 x 2 y 1
 z i .
 5 5
 2 2
 2x y 8 x 2y 1 
 Vì z 2 nên 4 .
 5 5 
 2 2
 x y 6x 4y 13 20.
 x 3 2 y 2 2 20 .
 Vây tập hợp biểu diễn số phức w là đường tròn tâm I 3; 2 .
 Cách 2.
 Đặt z a bi;w x yi .
 Vì z 2 nên a2 b2 4 .
 Ta có w 3 2i 2 i z .
 x yi 2i 3 2 i a bi .
 x 3 y 2 i 2a b 2b a i .
 x 3 2 y 2 2 2a b 2 2b a 2 .
 2 2
 x 3 y 2 5 a2 b2 .
 Trang 5 TÀI LIỆU ÔN THI THPTQG
 A. r 1. B. r 5. C. r 2. . D. r 3..
 Lời giải
 z
 Ta có: 1 z i 2 5 .
 i 2
 Suy ra tập hợp các điểm biểu diễn số phức z là một đường tròn có bán kính r 5.
Câu 16. (KTNL GV Bắc Giang 2019) Trong mặt phẳng tọa độ điểm biểu diễn số phức z thỏa mãn 
 z 1 2i 3 là
 A. đường tròn tâm I(1;2) , bán kính R 9. B. đường tròn tâm I(1;2) , bán kính R 3.
 C. đường tròn tâm I( 1; 2) , bán kính R 3. D. đường thẳng có phương trình x 2y 3 0 .
 Lời giải
 Chọn C
 Giả sử điểm M(x; y) là điểm biểu diễn số phức z . Ta có:
 z 1 2i 3 (x 1) (y 2)i 3 (x 1)2 (y 2)2 9
 2 2
 Vậy điểm M(x; y) thuộc đường tròn (x 1) (y 2) 9 có tâm I(1;2) , bán kính R 3.
Câu 17. (Sở Thanh Hóa 2019) Xét các số phức z thỏa mãn (2 z)(z i) là số thuần ảo. Tập hợp các 
 điểm biểu diễn của z trong mặt phẳng tọa độ là:
 1 5
 A. Đường tròn tâm I 1; ,bán kính R .
 2 2
 1 5
 B. Đường tròn tâm I 1; ,bán kính R .
 2 2
 C. Đường tròn tâm I 2;1 ,bán kính R 5 .
 1 5
 D. Đường tròn tâm I 1; ,bán kính R nhưng bỏ điểm A(2;0); B(0;1) .
 2 2
 Lời giải
 Gọi số phức z x yi x, y ¡ z x yi.
 Thay vào điều kiện ta được:
 (2 z)(z i).
 (2 x yi)(x yi i).
 2 x yi x 1 y i .
 (2 x)x y(1 y) (2 x)(1 y) xyi.
 (2 z)(z i) là số thuần ảo khi và chỉ khi:
 (2 x)x y(1 y) 0 .
 x2 y2 2x y 0.
 1 5
 Vậy số phức z x yi thuộc đường tròn tâm I 1; ,bán kính R .
 2 2
Câu 18. (Chuyên Bắc Giang 2019) Tìm tập hợp điểm biểu diễn số phức z thỏa mãn z i (1 i)z .
 Trang 7