Chuyên đề Ôn thi THPTQG - Chuyên đề 32: Ứng dụng hình học giải tích trong không gian

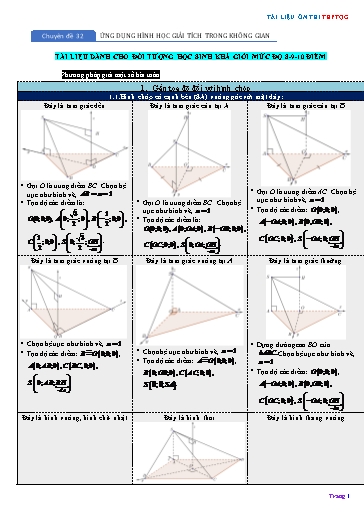
 TÀI LIỆU ÔN THI THPTQG
 Chuyên đề 32 ỨNG DỤNG HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
 TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ GIỎI MỨC ĐỘ 8-9-10 ĐIỂM
 Phương pháp giải một số bài toán
 1. Gắn tọa độ đối với hình chóp
 1.1.Hình chóp có cạnh bên (SA) vuông góc với mặt đáy:
 Đáy là tam giác đều Đáy là tam giác cân tại A Đáy là tam giác cân tại B
▪ Gọi O là trung điểm BC. Chọn hệ 
 trục như hình vẽ, AB a 1. ▪ Gọi O là trung điểm AC. Chọn hệ 
▪ Tọa độ các điểm là: ▪ Gọi O là trung điểm BC. Chọn hệ trục như hình vẽ, a 1.
 ▪ Tọa độ các điểm: O 0;0;0 , 
 3 1 trục như hình vẽ, a 1.
 O(0;0;0), A 0; ;0 , B ;0;0 , ▪ Tọa độ các điểm là: 
 2 2 A OA;0;0 , B 0,OB;0 ,
 O(0;0;0), A 0;OA;0 , B OB;0;0 ,
 1 3 C OC;0;0 , S OA;0;OH .
 C ;0;0 , S 0; ;OH . 
 C OC;0;0 , S 0;OA;OH . SA
 2 2 SA 
 SA 
 Đáy là tam giác vuông tại B Đáy là tam giác vuông tại A Đáy là tam giác thường
▪ Chọn hệ trục như hình vẽ, a 1. ▪ Dựng đường cao BO của 
▪ Tọa độ các điểm: B  O 0;0;0 , ▪ Chọn hệ trục như hình vẽ, a 1. ABC.Chọn hệ trục như hình vẽ, 
 ▪ Tọa độ các điểm: A  O 0;0;0 ,
 A 0; AB;0 , C BC,0;0 , a 1.
 B 0;OB;0 , C AC;0;0 , ▪ Tọa độ các điểm: O 0;0;0 , 
 S 0; AB; BH . S 0;0;SA . A OA;0;0 , B 0,OB;0 ,
 SA 
 C OC;0;0 , S OA;0;O H .
 SA 
 Đáy là hình vuông, hình chữ nhật Đáy là hình thoi Đáy là hình thang vuông
 Trang 1 TÀI LIỆU ÔN THI THPTQG
 AO 0;0;0 , O 0;0;0 ,
 B 0;AB;0 , A OA;0;0 ,
 C AD; AB;0 , B 0;OB;0 ,
 D AD;0;0 , C OC;0;0 ,
 A 0;0; AA , D 0; OD;0 ,
 B 0; AB; AA , A OA;0; AA ,
C AD; AB; AA , D AD;0; AA . B 0;OB; AA , C OC;0;CC , D 0; OD; DD 
 Lăng trụ tam giác đều Lăng trụ đứng có đáy tam giác thường
 Gọi O là trung điểm một Vẽ đường cao CO 
 cạnh đáy, chọn hệ trục trong tam giác ABC 
 như hình vẽ với a = 1. Ta và chọn hệ trục như 
 có: hình vẽ với a = 1.
 AB Tọa độ điểm là:
 O 0;0;0 , A ;0;0 ,
 2 O 0;0;0 , A OA;0;0 ,
 AB B OB;0;0 ,
 B ;0;0 , C 0;OC;0 ,
 2 C 0;OC;0 ,
 A OA;0;AA , A OA;0;AA ,
 AB 
B ;0;BB , C 0;OC;CC . B OB;0;BB , C 0;OC;CC .
 2 
 2.2.Lăng trụ nghiêng:
 Lăng trụ nghiêng có đáy là tam giác đều, hình chiếu Lăng trụ nghiêng có đáy là hình vuông hoặc hình 
 của đỉnh trên mặt phẳng đối diện là trung điểm một chữ nhật, hình chiếu của một đỉnh là một điểm 
 cạnh tam giác đáy thuộc cạnh đáy không chứa đỉnh đó
▪ Dựng hệ trục như hình vẽ, ta dễ dàng xác định được các ▪ Dựng hệ trục như hình vẽ, ta dễ dàng xác định được 
 điểm O, A , B , C , A. các điểm O, A , B , C , D , A. 
 ▪ Tìm tọa độ các điểm còn lại thông qua hệ thức vectơ 
▪ Tìm tọa độ các điểm còn  lại thông qua hệ thức vectơ     
 bằng nhau: AA BB CC . bằng nhau: AA BB CC DD .
 Dạng 1. Ứng dụng hình học giải tích OXYZ để giải quyết bài toán tìm GÓC
 Câu 1. (Mã 103 2018) Cho hình lập phương ABCD.A B C D có tâm O . Gọi I là tâm của hình vuông 
 A B C D và điểm M thuộc đoạn OI sao cho MO 2MI (tham khảo hình vẽ). Khi đó sin của góc tạo 
 bởi hai mặt phẳng MC D và MAB bằng
 Trang 3 TÀI LIỆU ÔN THI THPTQG
 Lời giải
 Không mất tính tổng quát ta đặt cạnh của khối lập phương là 1.
 Chọn hệ trục tọa độ sao cho A (0;0;0), B (1;0;0), D (0;1;0) và A(0;0;1) (như hình vẽ).
 1 1 1 
 Khi đó ta có: M ; ; .
 2 2 3 
   1 1 2   2 1 
 Suy ra: AB (1;0;0), MA ; ; AB, MA 0; ; n1 (0; 4;3) là VTPT của mặt 
 2 2 3 3 2 
 phẳng (MAB).
   1 1 1   1 1 
 D C (1;0;0), MD ; ; D C , MD 0; ; n2 (0;2; 3) là VTPT của mặt 
 2 2 3 3 2 
 phẳng (MC D ) .
 cosin của góc giữa hai mặt phẳng (MAB) và (MC D ) bằng:
 n .n 0.0 4.2 3.( 3) 17 13
 cos(n ,n ) 1 2 .
 1 2 2 2 2 2 2 2
 n1 . n2 0 ( 4) 3 . 0 2 ( 3) 65
Câu 3. (THPT Hùng Vương Bình Phước 2019) Cho hình hộp chữ nhật ABCD.A B C D , có 
 AB a, AD a 2, góc giữa A C và mặt phẳng ABCD bằng 30 . Gọi H là hình chiếu vuông góc 
 Trang 5 TÀI LIỆU ÔN THI THPTQG
 3 6 5 2
 A. .B. .C. .D. .
 7 7 7 7
 Lời giải
 Chú ý: Ta có thể giải bài toán với cạnh hình vuông a 1.
 Gọi O, M lần lượt là trung điểm của AB,CD . Vì SAB là tam giác đều và SAB vuông góc với 
 ABCD nên SO  ABCD .
 1 3 
 Xét hệ trục Oxyz có O 0;0;0 , M 1;0;0 , A 0; ;0 , S 0;0; . Khi đó 
 2 2 
 1 1 
 C 1; ;0 , D 1; ;0 .
 2 2 
  1 3   1 3  
 Suy ra SA 0; ; , AC 1; 1;0 , SC 1; ; ,CD 0;1;0 .
 2 2 2 2 
    3 3 1 
 Mặt phẳng SAC có véc tơ pháp tuyến n SA, AC ; ; .
 1 
 2 2 2 
    3 
 Mặt phẳng SAD có véc tơ pháp tuyến n SC,CD ;0;1 .
 1 
 2 
   
 n1.n2 5
 Vậy cos   .
 7
 n1 . n2
Câu 5. (Chuyên Sơn La 2019) Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a , tâm 
 a 6
 O . Gọi M và N lần lượt là trung điểm của hai cạnh SA và BC , biết MN . Khi đó giá trị sin của 
 2
 góc giữa đường thẳng MN và mặt phẳng SBD bằng
 2 3 5
 A. . B. . C. . D. 3 .
 5 3 5
 Lời giải
 Trang 7