Chuyên đề Ôn thi THPTQG - Chuyên đề 23: Mặt cầu, khối cầu (Mức 9-10 điểm)

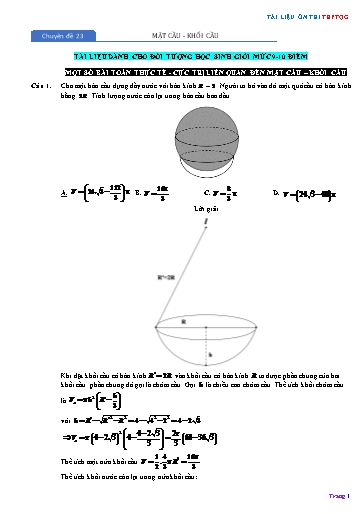
 TÀI LIỆU ÔN THI THPTQG
 Chuyên đề 23 MẶT CẦU - KHỐI CẦU
 TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH GIỎI MỨC 9-10 ĐIỂM
 MỘT SỐ BÀI TOÁN THỰC TẾ - CỰC TRỊ LIÊN QUAN ĐẾN MẶT CẦU – KHỐI CẦU
Câu 1. Cho một bán cầu đựng đầy nước với bán kính R 2 . Người ta bỏ vào đó một quả cầu có bán kính 
 bằng 2R . Tính lượng nước còn lại trong bán cầu ban đầu.
 112 16 8
 A. V 24 3 . B. V . C. V . D. V 24 3 40 .
 3 3 3 
 Lời giải
 I
 R'=2R
 R
 h
 Khi đặt khối cầu có bán kính R 2R vào khối cầu có bán kính R ta được phần chung của hai 
 khối cầu. phần chung đó gọi là chỏm cầu. Gọi h là chiều cao chỏm cầu. Thể tích khối chỏm cầu 
 2 h 
 là Vc h R .
 3 
 với h R R 2 R2 4 42 22 4 2 3 .
 2 4 2 3 2 
 V 4 2 3 4 64 36 3 .
 c 
 3 3
 1 4 16 
 Thể tích một nửa khối cầu V . R3 .
 2 3 3
 Thể tích khối nước còn lại trong nửa khối cầu:
 Trang 1 TÀI LIỆU ÔN THI THPTQG
 28a3
 S 2 Rl 2 R2 2 2 R2 với R 0
 R
 28a3 
 3
 S 2 2 2R 0 R a 14
 R 
 Bảng biến thiên
 3
 Vậy Smin R a 14
Câu 4. (Mã 104 2017) Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng 9, tính 
 thể tích V của khối chóp có thể tích lớn nhất.
 A. V 576 2 B. V 144 6 C. V 144 D. V 576
 Lời giải
 Chọn D
 S
 h l
 K
 I
 A
 B
 H R
 x
 D
 C
 Xét hình chóp tứ giác đều S.ABCD nội tiếp mặt cầu có tâm I và bán kính R 9.
 Gọi H AC  BD , K là trung điểm SC .
 Đặt AB x;SH h , x,h 0 .
 x x2
 Ta có HC l SC h2 .
 2 2
 SK SI
 Do SHI ∽ SHC l 2 2h.R x2 36h 2h2 .
 SH SC
 2 1 2 1 2
 Diện tích đáy của hình chóp SABCD x nên V h.x h 36h 2h .
 3 3
 3
 1 2 1 1 h h 36 2h 
 Ta có h. 36h 2h .h.h 36 2h . 576 V 576 , dấu bằng xảy ra 
 3 3 3 3 
 khi h h 36 2h h 12, x 12 . Vậy Vmax 576 .
Câu 5. (Sở Vĩnh Phúc 2019) Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng 
 9 , khối chóp có thể tích lớn nhất bằng bao nhiêu ?
 A. 576 2 . B. 144. C. 576 . D. 144 6 .
 Lời giải
 Trang 3 TÀI LIỆU ÔN THI THPTQG
 Bốn điểm O, A, B,C tạo thành 1 tam diện vuông.
 OA2 OB2 OC 2
 Bán kính mặt cầu ngoại tiếp tứ diện O.ABC là R .
 2
 Đặt OA a;OB b,a,b 0. Ta có a b 1 b 1 a .
 2 2 2
 OA2 OB2 OC 2 a2 b2 12 a 1 a 1
 Vậy R 
 2 2 2
 2
 1 3 
 2 a 
 2 4 6
 .
 2 4
 6 1
 Vậy R , tại a b ..
 min 4 2
Câu 7. (KTNL GV THPT Lý Thái Tổ 2019) Cho hình chóp S.ABCD có đáy ABCD là hình bình 
 hành, các cạnh bên của hình chóp bằng 6 cm , AB 4 cm . Khi thể tích khối chóp S.ABCD đạt 
 giá trị lớn nhất, tính diện tích mặt cầu ngoại tiếp S.ABCD .
 A. 12 cm2 . B. 4 cm2 . C. 9 cm2 . D. 36 cm2 .
 Lời giải
 Chọn D
 Trang 5 TÀI LIỆU ÔN THI THPTQG
 Gọi H là trung điểm của AC , Vì tam giác ABC vuông
 cân tại B và DA DB DC nên DH  (ABC) và tâm
 I của mặt cầu (S) thuộc tia DH . Đặt DH x và AH a
 ( 0 a 5,0 x 10 ).
 Có ID IA 5 và IH x 5 .
 Xét tam giác vuông AIH có a2 AH 2 AI 2 IH 2 25 (x 5)2 10x x2 .
 1
 Diện tích tam giác ABC là: S AC.BH a2 10x x2 .
 2
 1 1
 Thể tích khối chóp ABCD là: V S .DH (10x x2 )x .
 3 ABC 3
 1 1
 Xét f (x) (10x x2 )x (10x2 x3 ) với 0 x 10 .
 3 3
 Lập bảng biến thiên cho hàm số f (x) ta được giá trị lớn nhất của hàm số f (x) trên nửa
 4000 20
 khoảng 0;10 ta có kết quả là tại x .
 81 3
 Vậy a 4000,b 81 nên a b 4081.
Câu 9. Trong không gian cho tam giác ABC có AB 2R, AC R,·CAB 1200 . Gọi M là điểm thay đổi 
 thuộc mặt cầu tâm B , bán kính R . Giá trị nhỏ nhất của MA 2MC là
 A. 4R . B. 6R . C. R 19 . D. 2R 7 .
 Lời giải
 Chọn C
 A
 D
 B
 C
 2 2
   2         
 2 2 2 BA MB 1 
 Ta có MA MB BA MB 2MB.BA BA MB BA 2MB BA .
 MB BA 2 
  
  1  2  BA
 MA2 2MB BA MA 2 MB .
 2 4
  
  BA    
 Gọi D là điểm thỏa mãn BD , khi đó MA 2 MB BD 2 MD 2MD .
 4
 Do đó MA 2MC 2 MC MD 2CD .
 19 19
 Lại có CD2 AC 2 AD2 2AC.AD cos120 R2 CD R .
 4 2
 Dấu bằng xảy ra khi M là giao điểm của đoạn CD với mặt cầu tâm B bán kính R .
 Vậy giá trị nhỏ nhất của MA 2MC là R 19.
Câu 10. Cho mặt cầu S có bán kính bằng 3 m , đường kính AB . Qua A và B dựng các tia At1, Bt2 
 tiếp xúc với mặt cầu và vuông góc với nhau. M và N là hai điểm lần lượt di chuyển trên 
 Trang 7 TÀI LIỆU ÔN THI THPTQG
 Gọi H , I lần lượt là tâm đường tròn ngoại tiếp tam giác OMN và tâm bán mặt cầu ngoại tiếp tứ 
 a2
 diện SOMN R2 OH 2 IH 2 OH 2 .
 4
 MN MN
 Áp dụng định lý hàm số sin trong tam giác OMN ta có 2OH OH .
 sin60 3
 Áp dụng định lý hàm số cosin trong tam giác OMN ta có 
 MN 2 OM 2 ON 2 2.OM.ONcosM· ON 
 2 2
 2 OM ON a
 OM 2 ON 2 OM.ON OM ON 3OM.ON a2 3 
 4 4
 a2 a2 a2 a2 a2 a2
 MN 2 3OH 2 R2 OH 2 
 4 4 4 4 3.4 3
 a
 Bán kính nhỏ nhất của mặt cầu ngoại tiếp tứ diện SOMN bằng .
 3
 4 a2
Tính diện tích của mặt cầu S có bán kính nhỏ nhất ngoại tiếp tứ diện SOMN là 4 R2 
 3
Câu 12. Cho tứ diện ABCD có hình chiếu của A lên mặt phẳng BCD là H nằm trong tam giác BCD . 
 Biết rằng H cũng là tâm của một mặt cầu bán kính 3 và tiếp xúc các cạnh AB, AC, AD . Dựng 
 hình bình hành AHBS . Tính giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp hình chóp S.BCD
 3 3 3
 A. 3. B. 3 3 . C. . D. .
 2 2
 Lời giải
 Chọn D
 Trang 9