Chuyên đề Ôn thi THPTQG - Chuyên đề 23: Mặt cầu, khối cầu (Mức 7-8 điểm)

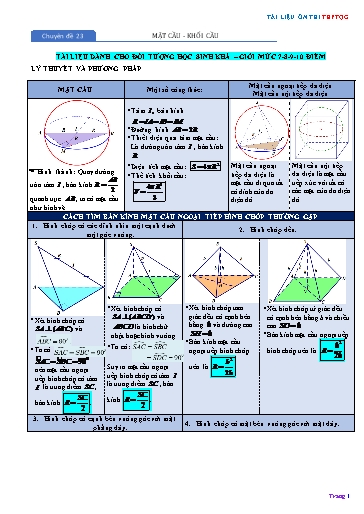
 TÀI LIỆU ÔN THI THPTQG
 Chuyên đề 23 MẶT CẦU - KHỐI CẦU
 TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ – GIỎI MỨC 7-8-9-10 ĐIỂM
LÝ THUYẾT VÀ PHƯƠNG PHÁP
 Mặt cầu ngoại tiếp đa diện
 MẶT CẦU Một số công thức:
 Mặt cầu nội tiếp đa diện
 ▪ Tâm I, bán kính 
 R IA IB IM .
 ▪ Đường kính AB 2R .
 ▪ Thiết diện qua tâm mặt cầu: 
 Là đường tròn tâm I , bán kính 
 R .
 ▪ Diện tích mặt cầu: S 4 R2 . Mặt cầu ngoại Mặt cầu nội tiếp 
Hình thành: Quay đường 
 ▪ Thể tích khối cầu: tiếp đa diện là đa diện là mặt cầu 
 AB mặt cầu đi qua tất tiếp xúc với tất cả 
tròn tâm I , bán kính R 4 R3
 2 V . cả đỉnh của đa các mặt của đa diện 
quanh trục AB , ta có mặt cầu 3 diện đó. đó.
như hình vẽ. 
 CÁCH TÌM BÁN KÍNH MẶT CẦU NGOẠI TIẾP HÌNH CHÓP THƯỜNG GẶP
1. Hình chóp có các đỉnh nhìn một cạnh dưới 
 2. Hình chóp đều.
 một góc vuông.
 ▪ Xét hình chóp có ▪ Xét hình chóp tam ▪ Xét hình chóp tứ giác đều 
 giác đều có cạnh bên 
▪ Xét hình chóp có SA  (ABCD) và có cạnh bên bằng b và chiều 
 bằng b và đường cao 
 SA  (ABC) và ABCD là hình chữ cao SO h .
 nhật hoặc hình vuông. SH h . ▪ Bán kính mặt cầu ngoại tiếp 
 · 0
 ABC 90 . ▪ Bán kính mặt cầu 2
 ▪ Ta có: S· AC S· BC b
▪ Ta có ngoại tiếp hình chóp hình chóp trên là R .
 · 0 2h
 S· AC S· BC 900 SDC 90 b2
 Suy ra mặt cầu ngoại trên là R .
 nên mặt cầu ngoại 2h
 tiếp hình chóp có tâm tiếp hình chóp có tâm I 
 I là trung điểm SC , là trung điểm SC , bán 
 SC SC
 bán kính R . kính R .
 2 2
 3. Hình chóp có cạnh bên vuông góc với mặt 
 4. Hình chóp có mặt bên vuông góc với mặt đáy.
 phẳng đáy.
 Trang 1 TÀI LIỆU ÔN THI THPTQG
 Lời giải
 A C 
 I M 
 B 
 O
 A C
 I M
 B
 Gọi I, I lần lượt là tâm hai đáy, O là trung điểm của II . Khi đó ta có O là tâm mặt cầu ngoại 
 tiếp lăng trụ.
 a 3 b
 Ta có: AI , IO suy ra bán kính mặt cầu ngoại tiếp lăng trụ là 
 3 2
 a2 b2 1
 R 4a2 3b2 
 3 4 2 3
 4 3 2 2 3
 Vậy V O;R R 4a 3b .
 3 18 3
Câu 3. Một mặt cầu ngoại tiếp hình hộp chữ nhật ABCD.A' B 'C ' D ' có kích thước AB 4a, 
 AD 5a, AA' 3a. Mặt cầu trên có bán kính bằng bao nhiêu?
 5 2a 3 2a
 A. . B. .6 a C. . 2 3a D. .
 2 2
 Lời giải
 Chọn A
 A' D'
 C'
 B'
 I
 A
 D
 B C
 Gọi I là tâm của hình hộp chữ nhật ABCD.A' B 'C ' D ' khi đó bán kính mặt cầu ngoại tiếp hình
 1 1 5 2a
 hộp này là R IA AC AB2 AD2 +A'A2 .
 2 2 2
Câu 4. (Chuyên Lê Hồng Phong Nam Định 2019) Thể tích khối cầu ngoại tiếp hình chữ nhật có ba 
 kích thước 1,2,3 là
 9 9 7 14 
 A. . B. . C. 36 . D. .
 8 2 3
 Lời giải
 Chọn D
 Trang 3 TÀI LIỆU ÔN THI THPTQG
 A’ D’
 B’ C’
 O
 A D
 B C
 Xét khối hộp chữ nhật ABCD.A B C D tâm O , với AB a , AD a 3 và AA 2a . Dễ thấy O 
 cách đều các đỉnh của khối hộp này nên mặt cầu ngoại tiếp khối hộp có tâm O , bán kính 
 AC 
 R .
 2
 Ta có
 AC 
 AC AB2 AD2 2a , AC AC 2 CC 2 2a 2 R a 2 .
 2
 Vậy diện tích mặt cầu ngoại tiếp khối hộp này là S 4 R2 8 a2 .
Câu 7. (Chuyên Đại học Vinh - 2019) Cho hình hộp chữ nhật ABCD.A B C D có AB a , 
 AD AA 2a . Diện tích của mặt cầu ngoại tiếp hình hộp đã cho bằng
 3 a2 9 a2
 A. 9 a2 . B. . C. . D. 3 a2 .
 4 4
 Lời giải
 Chọn A
 Ta có tâm mặt cầu ngoại tiếp hình hộp ABCD.A B C D cũng là trung điểm của một đường chéo 
 A C (giao các đường chéo) của hình hộp.
 Hình hộp chữ nhật có độ dài 3 cạnh dài, rộng, cao là: AD 2a , AB a , AA 2a .
 A C AD2 AB2 AA 2 3a
 Bán kính mặt cầu ngoại tiếp hình hộp là: R .
 2 2 2
 2
 2 3a 2
 Smc 4 R 4 . 9 a .
 2 
Câu 8. Cho hình lập phương có cạnh bằng a . Thể tích khối cầu ngoại tiếp hình lập phương đó bằng
 4 3 a3 3 a3 3
 A. V a3 . B. V 4 3 a3 . C. V . D. V .
 3 3 2
 Lời giải
 Chọn D
 Trang 5 TÀI LIỆU ÔN THI THPTQG
 Lời giải
 Chọn C
 B C
 a
 a
 a
 A D
 I
 B' C'
 A' a D'
 Gọi I là trung điểm của AC ' .
 Ta có ABC vuông tại B ( vì AB  (BB 'C 'C) ) và AB C vuông tại B (vì B C  (ABB A ) ).
 Khi đó IA IB IB IC , suy ra I là tâm mặt cầu ngoại tiếp tứ diện ABB C .
 a 3
 AC AB '2 B C 2 AB2 BB 2 B C 2 a 3. Vậy R .
 2
 Cách khác: Mặt cầu ngoại tiếp tứ diện ABB C cũng là mặt cầu ngoại tiếp tứ diện hình lập 
 phương ABCD.A B C D . Bán kính mặt cầu là nửa đường chéo hình lập phương cạnh a , tức là 
 a 3
 bằng .
 2
Câu 11. (Chuyên Quốc Học Huế 2019) Cho lăng trụ đứng ABC.A B C có đáy là tam giác ABC vuông 
 cân tại A , AB a , AA a 3 . Tính bán kính R của mặt cầu đi qua tất cả các đỉnh của hình lăng 
 trụ theo a .
 a 5 a a 2
 A. R . B. R . C. R 2a . D. R .
 2 2 2
 Lời giải
 Chọn A
 Hình vẽ.
 Gọi M là trung điểm BC , suy ra M là tâm đường tròn ngoại tiếp tam giác ABC .
 Gọi M là trung điểm B C , suy ra M là tâm đường tròn ngoại tiếp tam giác A B C .
 Gọi I là trung điểm MM , khi đó I chính là tâm đường tròn ngoại tiếp lăng trụ.
 Trang 7