Chuyên đề Ôn thi THPTQG - Chuyên đề 13: Tỉ số thể tích (Mức 7-10 điểm)

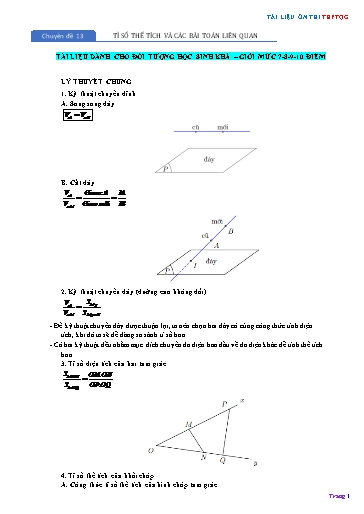
 TÀI LIỆU ễN THI THPTQG
Chuyờn đề 13 TỈ SỐ THỂ TÍCH VÀ CÁC BÀI TOÁN LIấN QUAN
 TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ – GIỎI MỨC 7-8-9-10 ĐIỂM
 Lí THUYẾT CHUNG
 1. Kỹ thuật chuyển đỉnh
 A. Song song đỏy
 Vcũ Vmới
 B. Cắt đỏy
 V Giaocũ IA
 cũ 
 Vmới Giao mới IB
 2. Kỹ thuật chuyển đỏy (đường cao khụng đổi)
 V S
 cũ đấy
 Vmới Sđấy mới
 - Để kỹ thuật chuyển đỏy được thuận lợi, ta nờn chọn hai đỏy cú cựng cụng thức tớnh diện
 tớch, khi đú ta sẽ dễ dàng so sỏnh tỉ số hơn.
 - Cả hai kỹ thuật đều nhằm mục đớch chuyển đa diện ban đầu về đa diện khỏc dễ tớnh thể tớch
 hơn.
 3. Tỉ số diện tớch của hai tam giỏc
 S OM.ON
 OMN 
 S APQ OP.OQ
 4. Tỉ số thể tớch của khối chúp
 A. Cụng thức tỉ số thể tớch của hỡnh chúp tam giỏc
 Trang 1 TÀI LIỆU ễN THI THPTQG
B. Mặt phẳng cắt cỏc cạnh bờn của lăng trụ tam giỏc
Gọi V1 , V2 và V lần lượt là thể tớch phần trờn, phần dưới và lăng trụ. Giả sử 
 AM CN BP
 m, n, p
 AA' CC' BB'
 m n p
Khi đú: V .V
 2 3
 AM CN
Khi M  A',N  C thỡ 1, 0
 AA' CC'
6. Khối hộp
A. Tỉ số thể tớch của khối hộp
Gọi V là thể tớch khối hộp, V 4 là thể tớch khối chúp tạo thành từ 4 trong 8 đỉnh của khối hộp. Khi 
đú:
 V
 V (hai đường chộo của hai mặt phẳng song song) 
 4 3
 V
 V (trường hợp cũn lại) 
 4 6
 V V
Vớ dụ: V ,V 
 A'C' BD 3 A'C' D' D 6
 Trang 3 TÀI LIỆU ễN THI THPTQG
 V 1 V 1 V 1 V 1
 A. SBMPN . B. SBMPN . C. SBMPN . D. SBMPN .
 VSABCD 16 VSABCD 6 VSABCD 12 VSABCD 8
 Lời giải
 Chọn B
 Dựng SO  MN I , SI  SD P , OE / /BP ;
 SP SI 1 DE DO 1
 Khi đú: I là tung điểm của MN, SO nờn ; 
 SE SO 2 DP DP 2
 SP 1
 Vậy: SP PE ED 
 SD 3
 V SP SM 1 1 1 V 1
 SMPB SMPB 
 VSADB SD SA 3 2 6 VSABCD 12
 V SP SN 1 1 1 V 1
 SNPB SNPB 
 VSCDB SD SC 3 2 6 VSABCD 12
 VSMPNB 1 1 1
 VSBMPN VSBMP VSBPN 
 VSABCD 12 12 6
Cõu 3. Cho tứ diện ABCD . Gọi B ,C lần lượt là trung điểm của AB và CD . Khi đú tỷ số thể tớch của 
 khối đa diện AB C D và khối tứ diện ABCD bằng
 1 1 1 1
 A. . B. . C. . D. .
 2 4 6 8
 Lời giải
 Chọn B
 Trang 5 TÀI LIỆU ễN THI THPTQG
 SP 1
 Suy ra SP PH HD .
 SD 3
 V 2V SM SP 1 1 1
 Theo cụng thức tỉ số thể tớch ta cú : S.BMPN S.BMP   ..
 VS.ABCD 2VS.BAD SA SD 2 3 6
Cõu 5. Cho hỡnh chúp S.ABCD cú đỏy ABCD là hỡnh bỡnh hành. Gọi K , M lần lượt là trung điểm của 
 cỏc đoạn thẳng SA , SB , ( ) là mặt phẳng qua K song song với AC và AM . Mặt phẳng ( ) 
 chia khối chúp S.ABCD thành hai khối đa diện. Gọi V1 là thể tớch của khối đa diện chứa đỉnh S 
 V1
 và V2 là thể tớch khối đa diện cũn lại. Tớnh tỉ số 
 V2
 V 7 V 5 V 7 V 9
 A. 1 = . B. 1 = . C. 1 = . D. 1 = .
 V2 25 V2 11 V2 17 V2 23
 Lời giải
 Chọn D
 Gọi V là thể tớch khối chúp S.ABCD ; I, H lần lượt là trung điểm SC, SM . Do ( ) / / (ACM ) 
 nờn ( ) cắt (SAD), (SBD), (SCD) lần lượt tại KL, HP, IJ cựng song song với OM .
 VB.HQP BH BQ BP 3 3 3 27 27 27 1 27
 Ta cú = . . = . . = . Suy ra VB.HQP = VB.SAC = . V = V .
 VB.SAC BS BA BC 4 2 2 16 16 16 2 32
 VA.KQL AK AQ AL 1 1 1 1 1 1 1 1
 = . . = . . = ị VA.KQL = VA.SBD = . V = V .
 VA.SBD AS AB AD 2 2 2 8 8 8 2 16
 1
 Tương tự: ị V = V .
 C.IPJ 16
 ổ ử
 ỗ27 1 1 ữ 23 9
 Do đú V2 = ỗ - - ữV = V ị V1 = V .
 ốỗ32 16 16ứữ 32 32
 V 9
 Vậy tỉ số 1 = .
 V2 23
Cõu 6. (THPT Hai Bà Trưng - Huế - 2019) Cho hỡnh chúp tứ giỏc đều S.ABCD . Mặt phẳng P qua 
 A và vuụng gúc với SC cắt SB, SC, SD lần lượt tại B , C , D . Biết C là trung điểm của SC . 
 V1
 Gọi V1,V2 lần lượt là thể tớch hai khối chúp S.AB C D và S.ABCD . Tớnh tỷ số .
 V2
 V 2 V 2 V 4 V 1
 A. 1 . B. 1 . C. 1 . D. 1 .
 V2 3 V2 9 V2 9 V2 3
 Lời giải
 Trang 7 TÀI LIỆU ễN THI THPTQG
 1 5 1 5 5 1
 A. x . B. x . C. x . D. x .
 2 2 3 3
 Lời giải
 Chọn B
 Ta cú:
 BC / / SAD SM SN
 SAD  BMC MN / /BC x .
 BC  BMC SA SD
 V 2V SM
 S.MBC S.MBC x
 VS.ABC V SA
 V 2V SM SN
 S.MCN S.MCN . x2
 VS.ACD V SA SD
 2 V V 2V V x x2
 S.MCN S.MBC x x2 S.MBCN x x2 S.MBCN 1 
 V V V 2
 V 1
 Mặt phẳng (MBC) chia khối chúp đó cho thành hai phần cú thể tớch bằng nhau S.MNBC 2 
 V 2
 5 1
 Từ 1 và 2 ta cú: 1 x x2 x .
 2
Cõu 9. Cho hỡnh chúp S.ABCD cú đỏy ABCD là hỡnh bỡnh hành. Gọi M , N lần lượt là trung điểm của 
 cỏc cạnh AB , BC . Điểm I thuộc đoạn SA . Biết mặt phẳng MNI chia khối chọp S.ABCD 
 7 IA
 thành hai phần, phần chứa đỉnh S cú thể tớch bằng lần phần cũn lại. Tớnh tỉ số k ?
 13 IS
 1 2 1 3
 A. . B. . C. . D. .
 2 3 3 4
 Lời giải
 Chọn B
 S
 E
 S
 I
 K E
 I
 P A D
 M
 B N C P
 A H D
 Q
 Hỡnh 1 Hỡnh 2
 Trang 9 TÀI LIỆU ễN THI THPTQG
 S
 2
 2
 2
 M B
 D
 2
 H E
 N
 2 10
 6
 A
 C
 o,
 Ta cú:
 • SA2 SB2 62 22 40 AB2 ãASB 90o .
 1
 • SBC vuụng tại B BN SC 2.
 2
 SN NB SB 2 SNB đều.
 Gọi D là điểm thuộc cạnh SA sao cho SD 2 , ta cú:
 DB2 22 22 8
 DN 2 22 22 2.2.2.cos120o 12
 NB2 4
 DB2 NB2 DN 2 DNB vuụng tại B .
 • Gọi H, E lần lượt là trung điểm của DN, NB, ta cú:
 NB  SE
 +) NB  SHE NB  SH .
 NB  HE
 SH  DN
 +) SH  DNB SDN  DNB D  M SM 2 .
 SH  NB
 V SM SN 2 2 1
 k S.BMN . . .
 VS.ABC SA SC 6 4 6
Cõu 11. (Đề tham khảo 2017) Cho khối tứ diện cú thể tớch bằng V . Gọi V là thể tớch của khối đa diện 
 V 
 cú cỏc đỉnh là cỏc trung điểm của cỏc cạnh của khối tứ diện đó cho, tớnh tỉ số .
 V
 V 1 V 1 V 2 V 5
 A. . B. . C. . D. .
 V 2 V 4 V 3 V 8
 Lời giải
 Chọn A
 Trang 11