Chuyên đề Ôn thi THPT Toán 12 - Chủ đề 5: Khối đa diện (Vận dụng cao)

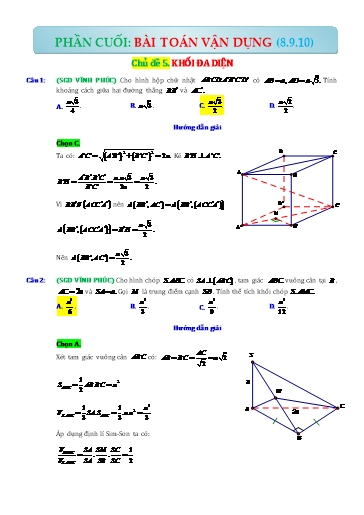
 PHẦN CUỐI: BÀI TOÁN VẬN DỤNG (8.9.10)
 Chủ đề 5. KHỐI ĐA DIỆN
Câu 1: (SGD VĨNH PHÚC) Cho hình hộp chữ nhật ABCD.A B C D có AB a, AD a 3. Tính 
 khoảng cách giữa hai đường thẳng BB và AC .
 a 3 a 3 a 2
 A. . B. a 3 . C. . D. .
 4 2 2
 Hướng dẫn giải
 Chọn C.
 2 2 D C
 Ta có: A C A B B C 2a. Kẻ B H  A C . 
 A
 A B .B C a.a 3 a 3 B
 B H . 
 B C 2a 2
 Vì BB // ACC A nên d BB , AC d BB , ACC A D' C'
 H
 a 3
 d BB , ACC A B H . A' B'
 2
 a 3
 Nên d BB , AC .
 2
Câu 2: (SGD VĨNH PHÚC) Cho hình chóp S.ABC có SA  ABC , tam giác ABC vuông cân tại B , 
 AC 2a và SA a. Gọi M là trung điểm cạnh SB . Tính thể tích khối chóp S.AMC.
 a3 a3 a3 a3
 A. . B. . C. . D. .
 6 3 9 12
 Hướng dẫn giải
 Chọn A.
 AC
 Xét tam giác vuông cân ABC có: AB BC a 2 S
 2
 1 2 a
 SABC AB.BC a 
 2 M
 1 1 a3 C
 V SA.S .a.a2 A 2a
 S.ABC 3 ABC 3 3
 Áp dụng định lí Sim-Son ta có:
 B
 VSAMC SA SM SC 1
 . . 
 VS.ABC SA SB SC 2 S
 K
 M
 N
 H
 4 2 D
 A
 B C
 SAB  ABCD , SAB  ABCD AB
 Theo giả thiết, ta có SA  ABCD .
 SA  AB
 Gọi N, H, K lần lượt là trung điểm các cạnh SA, SB và đoạn SH . 
 BC  SA
 Ta có BC  SAB BC  AH .
 BC  AB
 Mà AH  SB (VABC cân tại A có AH là trung tuyến).
 Suy ra AH  SBC , do đó KN  SBC (vì KN || AH , đường trung bình).
 Mặt khác MN || BC MN || SBC .
 1
 Nên d M , SBC d N, SBC NK AH 2 2 . 
 2
 Đáp án: B.
Câu 5: (NGUYỄN KHUYẾN TPHCM) Cho tứ diện đều ABCD có cạnh bằng 3. Gọi M , N lần lượt là 
 trung điểm các cạnh AD, BD. Lấy điểm không đổi P trên cạnh AB (khác A, B ). Thể tích 
 khối chóp PMNC bằng
 9 2 8 3 27 2
 A. B. C. 3 3 D. 
 16 3 12
 Hướng dẫn giải
 A
 Chọn A
 Do AB P CMN nên d P, CMN d A, CMN d D, CMN 
 M
 P
 1
 Vậy V V V V
 PCMN DPMN MCND 4 ABCD
 N
 B D
 (Do diện tích đáy và chiều cao đều bằng một nửa).
 C AHC ' vuông cân tại H.
 AC ' 8a
 AH 4a 2. 
 2 2
 2
 2 2 2 2a 2 . 3 16a3 6
 NX: V V AH.S .4a 2. .
 A.BCC 'B' 3 ABC.A'B'C ' 3 ABC 3 4 3
Câu 8: (T.T DIỆU HIỀN) Cho hình lập phương ABCD.A' B 'C ' D ' cạnh a . Tính khoảng cách giữa 
 hai đường thẳng BC ' và CD ' .
 a 3 a 2
 A. a 2 . B. . C. 2a . D. .
 3 3
 Hướng dẫn giải
 Chọn B
 A' D'
 O
 B' C'
 H
 A
 D
 B C
 Gọi O A'C ' B ' D ' và từ B ' kẽ B ' H  BO
 Ta có CD ' // (BA'C ') nên 
 BB '.B 'O a 3
 d(BC ';CD ') d(D ';(BA'C ')) d(B ';(BA'C ')) B ' H 
 BO 3
Câu 9: (T.T DIỆU HIỀN) Một hình hộp chữ nhật ABCD.A B C D có ba kích thước là 2cm , 3cm và 
 6cm . Thể tích của khối tứ diện A.CB D bằng
 A. 8 cm3 . B. 12 cm3 . C. 6 cm3 . D. 4 cm3 .
 Hướng dẫn giải
 Chọn B. 
 A' D'
 Ta có : 
 B'
 C'
 6 cm
 A
 D
 3 cm
 B 2 cm C D' C'
 30°
 A' B'
 x
 D C
 O y
 A B
 • Đặt x CD; y BC x y 
 • Áp dụng định lý hàm cos và phân giác trong tam giác BCD
 3a2 x2 y2 xy và x2 y2 5a2 
 x 2a; y a 
 • Với x 2y 2a và Cµ 60 BD  AD B·D ';(ADD'A') 30 DD ' 3a 
 2
 • SABCD xy.sin 60 a 3
 • Vậy V hình hộp = a33 3
 2
Câu 12: (NGÔ GIA TỰ - VP) Cho hình chóp tứ giác đều S.ABCD có thể tích V . Gọi M là 
 6
 trung điểm của cạnh SD . Nếu SB  SD thì khoảng cách từ B đến mặt phẳng MAC 
 bằng:
 1 1 2 3
 A. . B. . C. . D. .
 2 2 3 4
 Hướng dẫn giải
 Chọn A
 S
 M
 D
 A
 O
 B C
 Giả sử hình chóp có đáy ABCD là hình vuông cạnh a . Khi đó, BD a 2 .
 BD a 2
 Tam giác SBD vuông cân tại S nên SD SB a và SO .
 2 2 D. V a b c.
 Hướng dẫn giải
 B C
 x a
 A
 y D
 b
 z c
 B' C'
 A' D'
 Chọn A.
 Giả sử hình hộp chữ nhật có ba kích thước: x, y, z .
 x2 y2 a2 y2 a2 x2 y2 a2 x2
 2 2 2 2 2 2 2 2 2 2 2
 Theo yêu cầu bài toán ta có y z c y z c a x b x c
 2 2 2 2 2 2 2 2 2
 x z b z b x z b x
 2 2 2
 2 a b c
 y 
 2
 2 2 2 a2 c2 b2 a2 b2 c2 b2 c2 a2
 2 a b c 
 x V 
 2 8
 2 2 2
 2 b c a
 z 
 2
Câu 15: (SỞ GD HÀ NỘI) Cho hình lăng trụ ABCA B C có đáy là tam giác đều cạnh a . Hình chiếu 
 vuông góc của A lên mặt phẳng ABC trùng với trọng tâm tam giác ABC . Biết khoảng 
 a 3
 cách giữa hai đường thẳng AA và BC bằng . Tính thể tích V của khối lăng trụ 
 4
 ABCA B C .
 a3 3 a3 3 a3 3 a3 3
 A. V . B. V . C. V . D. V .
 24 12 3 6
 Hướng dẫn giải 
 Chọn B.
 A' C'
 M là trung điểm của BC thì BC  AA M .
 H
 B'
 Gọi MH là đường cao của tam giác A AM thì
 C
 MH  A A và HM  BC nên HM là khoảng cách A
 G
 M
 B