Chuyên đề Hình thang, hình thang cân và hình thang vuông Toán 8

 GV: Thạc sĩ Bùi Đức Phương – SĐT 0906 434 811 Facebook: https://www.facebook.com/feo.pro 
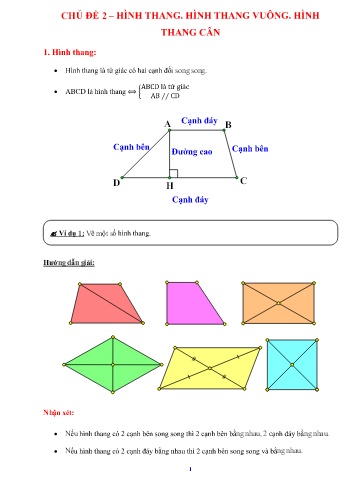
 CHỦ ĐỀ 2 – HÌNH THANG. HÌNH THANG VUÔNG. HÌNH 
 THANG CÂN 
1. Hình thang: 
 • Hình thang là tứ giác có hai cạnh đối song song. 
 ABCD là tứ giác
 • ABCD là hình thang ⟺ { 
 AB ∕∕ CD
 A Cạnh đáy B
 Cạnh bên
 Đường cao Cạnh bên
 D H C
 Cạnh đáy
  Ví dụ 1: Vẽ một số hình thang. 
Hư ớng dẫn giải: 
Nhận xét: 
 • Nếu hình thang có 2 cạnh bên song song thì 2 cạnh bên bằng nhau, 2 cạnh đáy bằng nhau. 
 • Nếu hình thang có 2 cạnh đáy bằng nhau thì 2 cạnh bên song song và bằng nhau. 
 1 
 GV: Thạc sĩ Bùi Đức Phương – SĐT 0906 434 811 Facebook: https://www.facebook.com/feo.pro 
Chứng minh: 
 AB // CD ⇒ Â1 = Ĉ2 
 AD // BC ⇒ Â2 = Ĉ1 
 Xét ∆ADC & ∆CBA có: Â1 = Ĉ2; Â2 = Ĉ1; AC chung 
 Suy ra ∆ADC = ∆CBA (g.c.g) ⇒ AD = BC; AB = CD 
Chứng minh nhận xét số 2: Nếu hình thang có 2 cạnh đáy bằng nhau thì 2 cạnh bên song song 
và bằng nhau. 
 Giả thiết Tứ giác ABCD 
 A B
 AB // CD; AB = CD 2 1
 Kết luận AD = BC; AD // BC 
 2 1
 D C
Chứng minh: 
 AB // CD ⇒ Â1 = Ĉ2 
 Xét ∆ADC & ∆CBA có: Â1 = Ĉ2; AC chung; AB = CD 
 Suy ra ∆ADC = ∆CBA (c.g.c) ⇒ AD = BC 
 ⇒ Â2 = Ĉ1 ⇒ AD // BC. 
 3 
 GV: Thạc sĩ Bùi Đức Phương – SĐT 0906 434 811 Facebook: https://www.facebook.com/feo.pro 
Chú ý: Kết luận tứ giác (hay tam giác) là hình gì phải sử dụng “suy ra” không được dùng “⇒” 
  Ví dụ 4: Hình thang vuông ABCD vuông tại A, D có AB = AD = 2 cm; CD = 4 cm. Tính 
 các góc của hình thang. 
 A 2 cm B
 2 cm
 D C
 4 cm
Hướng dẫn giải: 
 A 2 cm B
 1
 2
 2 cm
 D C
 H
 4 cm
 Dựng BH ⊥ CD với H ∈ CD 
 BH ⊥ CD 
 } suy ra AD // BH 
 AD ⊥ CD 
 Hình thang ABHD có AD // BH nên theo nhận xét Nếu hình thang có 2 cạnh bên song song 
 thì 2 cạnh bên bằng nhau, 2 cạnh đáy bằng nhau ta có: 
 DC 4
 AD = BH = 2 cm & DH = HC = = = 2 cm 
 2 2
 5 
 GV: Thạc sĩ Bùi Đức Phương – SĐT 0906 434 811 Facebook: https://www.facebook.com/feo.pro 
Hướng dẫn giải: 
 a) Tìm các hình thang cân + b) Tính các góc còn lại của mỗi hình thang cân đó. 
 Hình a) 
 Ta có Â + B̂ = 80° + 100° = 180° (Hai góc 
 A B
 trong cùng phía bù nhau) nên AB // CD. 
 80° 80°
 Suy ra ABCD là hình thang. 
 Ta có Â = B̂ = 80° (Hai góc kề một đáy bằng 
 100°
 nhau). 
 C D
 Do đó ABCD là hình thang cân. 
 Vì ABCD là hình thang cân nên Ĉ = D̂ = 80° 
 (Hai góc kề một đáy bằng nhau). 
 Hình b) 
 Ta có Ĝ + F̂ = 80° + 110° = 190° (Hai góc ở 
 E
 vị trị trong cùng phía) nên EF không song song F
 với GH. 110°
 80° 80°
 G H
 7 
 GV: Thạc sĩ Bùi Đức Phương – SĐT 0906 434 811 Facebook: https://www.facebook.com/feo.pro 
4.2. Tính chất: 
Định lý 1: Trong hình thang cân, hai cạnh bên bằng nhau. 
 Giả thiết Tứ giác ABCD Giả thiết ABCD hình thang cân 
 AB // CD; Ĉ = D̂ Hoặc (AB // CD) 
 Kết luận AD = BC Kết luận AD = BC 
CHỨNG MINH 
Trường hợp 1: Hai cạnh bên không song song. 
 S
 A 1 1 B
 2 2
 D C
 Gọi S là giao điểm của AD và BC. 
 ABCD hình thang cân ⇒ D̂ = Ĉ ⇒ ∆SDC cân ⇒ SD = SC (1) 
 ABCD hình thang cân ⇒ Â2 = B̂2 
 ⇒ 180° − Â1 = 180° − B̂1 ⇒ Â1 = B̂1 
 ⇒ ∆SAB cân ⇒ SA = SB (2) 
 Từ (1)(2) suy ra SD − SA = SC − SB ⇒ AD = BC 
 9 
 GV: Thạc sĩ Bùi Đức Phương – SĐT 0906 434 811 Facebook: https://www.facebook.com/feo.pro 
CHỨNG MINH 
 ̂ ̂
 ABCD hình thang cân ⇒ { D = C 
 AD = BC
 Xét ∆ADC & ∆BCD có: 
 ADĈ = BCD̂; AD = BC; DC chung 
 Suy ra ∆ADC = ∆BCD (c.g.c) ⇒ AC = BD 
Định lý 3: Hình thang có hai đường chéo bằng nhau là hình thang cân. 
Yêu cầu HS vẽ một hình thang và viết GT-KL và chứng minh định lý 3. 
 Giả thiết Tứ giác ABCD Giả thiết ABCD hình thang (AB // CD) 
 AB // CD; AC = BD Hoặc AC = BD 
 Kết luận Ĉ = D̂ Kết luận ABCD hình thang cân 
 A B
 1 1
 D C E
HƯỚNG DẪN CHỨNG MINH 
 Để chứng minh ABCD hình thang cân ⇒ chứng minh ADĈ = BCD̂ ⇒ chứng minh ∆ADC = 
 ∆BCD 
 Để chứng minh ∆ADC = ∆BCD ta đã có: AC = BD; DC chung ⇒ Cần chứng minh D̂1 = Ĉ1 
 HD: Kẻ đường thẳng qua B song song với AC cắt DC tại E. 
 ⇒ AC = BD (hình thang có 2 cạnh bên song song thì 2 cạnh bên bằng nhau) 
 11 
 GV: Thạc sĩ Bùi Đức Phương – SĐT 0906 434 811 Facebook: https://www.facebook.com/feo.pro 
Chú ý: Hình thang có 2 cạnh bên bằng nhau KHÔNG PHẢI là hình thang cân NHƯNG hình thang 
cân thì có 2 cạnh bên bằng nhau. 
4.4. Cách vẽ hình thang cân 
Cách vẽ 1: Cắt một tam giác cân bởi một cát tuyến không đi qua đỉnh và song song với đáy. (Sẽ được 
chứng minh ở  BÀI TẬP TỰ ÔN TẬP) 
 C
 F E
 A B A B
Cách vẽ 2: Vẽ hai đường thẳng song song , và lấy một đoạn thẳng AB nằm trên một đường thẳng 
ví dụ là đường thẳng . Từ A, B vẽ hai đường tròn có cùng bán kính sao cho nó cắt đường thẳng . 
Ta được hai hình thang cân là ABED và ABFC. 
 a C D E F
 b
 A B
 13 
 GV: Thạc sĩ Bùi Đức Phương – SĐT 0906 434 811 Facebook: https://www.facebook.com/feo.pro 
 ACD̂ = Ĉ1 + Ĉ2 = 45° + 45° = 90° ⇒ CD ⊥ AC (1) 
 ∆ABC vuông cân ở A ⇒ Â = 90° ⇒ AB ⊥ AC (2) 
 Từ (1)(2) suy ra CD // AB 
 Suy ra tứ giác ABDC là hình thang. 
 Hình thang ABDC có Â = 90° nên là hình thang vuông. 
 Vậy tứ giác ABDC là hình thang vuông ở C, D. 
  Bài 2: Cho hình thang ABCD (AB // CD) có ACD̂ = BDĈ. Chứng minh ABCD là hình thang 
 cân. 
Hướng dẫn giải: 
 D C
 1 1
 O
 1 1
 A B
 Vì AB // CD nên ta có Ĉ1 = Â1 và B̂1 = D̂1. 
 Mặt khác Ĉ1 = D̂1 nên ta có Â1 = B̂1. 
 Ta có Ĉ1 = D̂1 nên ∆ODC cân tại O ⇒ OD = OC. 
 Tương tự Â1 = B̂1 nên ∆OAB cân tại O ⇒ OA = OB. 
 Suy ra OA + OC = OB + OD hay AC = BD. 
 Hình thang ABCD (AB // CD) có AC = BD nên ABCD là hình thang cân. 
 15