Chuyên đề Hình học trực quan Toán 6 theo chương trình SGK mới

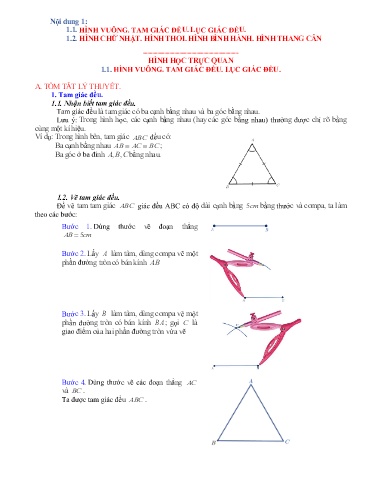
 Nội dung 1: 
 1.1. HÌNH VUÔNG. TAM GIÁC ĐỀU. LỤC GIÁC ĐỀU. 
 1.2. HÌNH CHỮ NHẬT. HÌNH THOI. HÌNH BÌNH HÀNH. HÌNH THANG CÂN 
 --------------------------------------- 
 HÌNH HỌC TRỰC QUAN 
 1.1. HÌNH VUÔNG. TAM GIÁC ĐỀU. LỤC GIÁC ĐỀU. 
A. TÓM TẮT LÝ THUYẾT. 
 1. Tam giác đều. 
 1.1. Nhận biết tam giác đều. 
 Tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng nhau. 
 Lưu ý: Trong hình học, các cạnh bằng nhau (hay các góc bằng nhau) thường được chỉ rõ bằng 
cùng một kí hiệu. 
Ví dụ: Trong hình bên, tam giác ABC đều có: 
 Ba cạnh bằng nhau AB AC BC ; 
 Ba góc ở ba đỉnh ABC,, bằng nhau. 
 1.2. Vẽ tam giác đều. 
 Để vẽ tam tam giác ABC giác đều ABC có độ dài cạnh bằng 5cm bằng thước và compa, ta làm 
theo các bước: 
 Bước 1. Dùng thước vẽ đoạn thẳng 
 AB 5 cm 
 Bước 2. Lấy A làm tâm, dùng compa vẽ một 
 phần đường tròn có bán kính AB 
 Bước 3. Lấy B làm tâm, dùng compa vẽ một 
 phần đường tròn có bán kính BA ; gọi C là 
 giao điểm của hai phần đường tròn vừa vẽ 
 Bước 4. Dùng thước vẽ các đoạn thẳng AC 
 và BC . 
 Ta được tam giác đều ABC . 
 Chu vi của hình vuông: Ca 4 ; 
 Diện tích của hình vuông: S a . a a2 . 
 3. Lục giác đều. 
 Hình ABCDEG ở là lục giác đều, có các đặc điểm sau: 
 Các tam giác OAB,,,,, OBC OCD ODE OEG OGA là tam giác đều nên các cạnh AB,,, BC CD DE,
 EG, GAcó độ dài bằng nhau. 
 Các đường chéo chính AD,, BE CG cắt nhau tại điểm O . 
 Các đường chéo chính AD,, BE CG có độ dài gấp đôi độ dài cạnh tam giác đều nên chúng bằng 
 nhau. 
 Mỗi góc ở đỉnh ABCDEG,,,,, của lục giác đều ABCDEG đều gấp đôi góc của một tam giác đều 
 nên chúng bằng nhau. 
Nhận xét: 
 Lục giác đều ABCDEG có: 
 Sáu cạnh bằng nhau: AB BC CD DE EG GA. 
 Ba đường chéo chính cắt nhau tại điểm O ; Ba đường chéo chính bằng nhau: AD BE CG ; sáu 
 góc ở các đỉnh ABCDEG,,,,, bằng nhau. 
 4. Các dạng toán thường gặp. 
 Dạng 1: Nhận dạng các hình: 
 Phương pháp giải: Áp dụng định nghĩa các hình: hình tam giác đều, hình vuông, hình lục giác đều. 
 Dạng 2: Vẽ hình: 
 Phương pháp giải: Áp dụng đúng các bước vẽ hình cơ bản: hình tam giác đều, hình vuông. 
 Dạng 3: Tính chu vi và diện tích các hình: 
 Phương pháp giải: Áp dụng công thức tính chu vi, diện tích các hình: hình tam giác đều, hình 
vuông, hình lục giác đều và thay số. 
B. BÀI TẬP TRẮC NGHIỆM. 
I – MỨC ĐỘ NHẬN BIẾT: 
Câu 1. Cho tam giác đều ABC . Khẳng định nào sau đây là đúng: 
 A. AB > AC > BC. 
 B. AB < AC < BC. 
 C. AB = AC = BC. 
 D. AB = AC < BC. 
Câu 2. Trong các hình dưới đây hình vẽ tam giác đều là: Câu 8. Cho hình vuông ABCD. Khẳng định nào sau đây là sai. 
 A. BC = AC 
 B. AB = CD 
 C. AC = BD 
 D. BD > AD 
Câu 9. Hình sau đây có bao nhiêu hình vuông. 
 A. 5 
 B. 6 
 C. 7 
 D. 8 
Câu 10. Hình sau đây có bao nhiêu hình vuông? 
 A. 6 hình vuông. 
 B. 7 hình vuông. 
 C. 8 hình vuông. 
 D. 9 hình vuông. 
III – MỨC ĐỘ VẬN DỤNG. 
Câu 11. Cho hình vẽ sau biết ABCDEF là hình lục giác đều, CD 5 cm . Độ dài đoạn thẳng AD là: 
 A.5cm 
 B.10cm 
 C.15cm 
 D. 20cm 
Câu 12. Một hình vuông có chu vi bằng 16cm, diện tích của hình vuông đó là: 
 A. 4.cm2 
 A. 15,7cm2 
 B. 157cm2 
 C. 78,5cm2 
 D. 314cm2 
Câu 20. Nối điểm chính giữa các cạnh hình vuông thứ nhất ta được hình vuông thứ hai. Nối điểm 
 chính giữa các cạnh hình vuông thứ hai ta được hình vuông thứ ba, và cứ tiếp tục như vậy. 
 Số hình tam giác có trong hình vẽ như vậy đến hình vuông thứ 4 là: 
 A. 12 hình tam giác. 
 B. 16 hình tam giác. 
 C. 20 hình tam giác. 
 D. 24 hình tam giác. 
C. BÀI TẬP TỰ LUẬN: 
I – MỨC ĐỘ NHẬN BIẾT: 
Bài 1. Hình dưới đây có phải là hình vuông không? Vì sao? 
Bài 2. Quan sát các hình sau và cho biết: Hình nào là hình tam giác đều, hình nào là hình vuông, hình 
nào là hình lục giác đều? 
Bài 4. Hình vẽ dưới đây có bao nhiêu hình vuông? 
Bài 5. Hình sau đây có bao nhiêu tam giác đều? 
III – MỨC ĐỘ VẬN DỤNG: 
Bài 1. Hãy xếp 9 que diêm giống hệt nhau thành 5 hình tam giác đều. 
Bài 2. Cho 11 que tính giống hệt nhau. Hãy dùng 11 que tính đó để tạo ra 6 tam giác đều. 
Bài 3. Hãy xếp que diêm giống hệt nhau thành 5 hình vuông. 
Bài 4. Hãy cắt một hình vuông thành 4 mảnh và ghép lại thành một hình tam giác. 
Bài 5. Hãy cắt một hình vuông thành 5 mảnh và ghép thành hai hình vuông. 
IV – MỨC ĐỘ VẬN DỤNG CAO: 
Bài 1. Bác Nam có 7 cây xanh muốn trồng trên một khu đất trống. Bác muốn trồng thành 6 hàng, mỗi 
hàng có 3 cây. Hỏi bác Nam phải trồng cây như thế nào? 
Bài 2. Thầy An muốn trồng 9 cây phượng trong vườn trường thành 8 hàng, mỗi hàng có 3 cây. Hỏi 
thầy An phải trồng như thế nào? 
Bài 3. Tháp tam giác là hình tam giác đều lớn cấu thành từ nhiều tam giác với nhiều tầng. Hỏi tháp tam 
giác với độ cao là 4 tầng có bao nhiêu hình tam giác. 
 D. HƯỚNG DẪN GIẢI CHI TIẾT BÀI TẬP TRẮC NGHIỆM 
 BẢNG ĐÁP ÁN BÀI TẬP TRẮC NGHIỆM 
 1 2 3 4 5 6 7 8 9 10 
 C C C A D A D A D A 
 11 12 13 14 15 16 17 18 19 20 
 A B C B D D B B C A 
 HƯỚNG DẪN GIẢI CHI TIẾT 
Câu 1. Cho tam giác đều . Khẳng định nào sau đây là đúng. 
 A. AB > AC > BC. 
 B. AB < AC < BC. 
 C. AB = AC = BC. 
 D. AB = AC < BC. 
 Lời giải 
 Chọn C 
 Tam giác đều có 3 cạnh bằng nhau. 
Câu 2. Trong các hình dưới đây hình vẽ tam giác đều là: 
 A. Hình a. 
 B. Hình b. 
 C. Hình c. 
 D. Hình d. 
 Lời giải 
 Chọn C 
 Tam giác đều có ba góc bằng nhau. 
Câu 3. Cho hình lục giác đều ABCDEF . Số tam giác đều có trong hình là: 
 ABC
 A. 4 tam giác đều. 
 B. 5 tam giác đều. 
 C. 6 tam giác đều. 
 D. 7 tam giác đều. 
 Lời giải 
 Chọn C 
 Hình lục giác đều được ghép từ 6 tam giác đều. 
Câu 4. Hãy khoanh tròn vào phương án đúng nhất trong các phương án sau: 
 A. Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau. Chọn A 
 Hình vuông có 2 đường chéo bằng nhau. 
Câu 9. Hình sau đây có bao nhiêu hình vuông. 
 A. 5 
 B.6 
 C. 7 
 D. 8 
 Lời giải 
 Chọn D 
 Hình trên có 8 hình vuông. 
Câu 10. Hình sau đây có bao nhiêu hình vuông? 
 A. 6 hình vuông. 
 B. 7 hình vuông. 
 C. 8 hình vuông. 
 D. 9 hình vuông. 
 Lời giải 
 Chọn A. 
 Trong hình đã cho có 4 vuông được ghép từ hai hình tam giác; 1 hình vuông được ghép từ 4 
hình tam giác và 1 hình vuông to bên ngoài. 
 Vậy hình đã cho có tất cả 6 hình vuông. 
III – MỨC ĐỘ VẬN DỤNG: 
Câu 11. Cho hình vẽ sau biết là hình lục giác đều, . Độ dài đoạn thẳng là: 
 A. 
 B. 
 C. 
 D. 
 Lời giải 
 Chọn B 
 Độ dài đường chéo chínhABCDEF gấp hai lần đường chéo phụ nênCD AD 5 cm BE CG 5.2 10 cmAD 
Câu 12. Một5cm hình vuông có chu vi bằng , diện tích của hình vuông đó là: 
 A. 10cm 
 B.1615cmcm2 . 
 C.3220cmcm2 . 
 D. 64cm2 . 16cm
 2
 4.cm Lời giải 2 . 2 4 m2 
 Diện tích còn lại là: 
 225 – 4 221 m2 
 Đáp số: 221m2. 
Câu 17. Một hình vuông có chu vi bằng 36 cm . Người ta kéo dài cạnh của hình vuông đó về bên phải 
 2 cm . Diện tích của hình sau khi mở rộng là: 
 A. 72 cm2. 
 B. 99 cm2. 
 C. 144 cm2. 
 D. 81 cm2. 
 Lời giải 
 Chọn B 
 Độ dài một cạnh của hình vuông lúc ban đầu là: 
 36 : 4 9 cm 
 Chiều dài của hình chữ nhật mới là: 
 9 2 11 cm 
 Diện tích của hình sau khi mở rộng là: 
 11 . 9 99 cm2 
 Đáp số: 99 cm2 . 
Câu 18. Để lát nền một phòng học hình chữ nhật người ta dùng loại gạch men hình vuông có cạnh 
 30cm . Hỏi cần bao nhiêu viên gạch để lát kín nền phòng học đó, biết rằng nền phòng học có 
 chiều rộng 6m và chiều dài 12m và phần mạch vữa không đáng kể? 
 A. 750 viên gạch. 
 B. 800viên gạch. 
 C. 900viên gạch. 
 D. 1000 viên gạch. 
 Lời giải 
 Chọn B. 
 Diện tích một viên gạch là: 
 30 . 30 900 (cm2 ) 
 Diện tích căn phòng đó là: 
 12 . 6 72 (m2 ) 
 72m22 720000 cm 
 Để lát kín nền căn phòng đó người ta cần dùng số viên gạch là: 
 720000:900 800 (viên gạch) 
 Đáp số: 800 viên gạch. 
Câu 19. Cho hình vẽ sau, biết các đỉnh của lục giác đều ABCDEF đều thuộc đường trònCD 5 cm . 
 Tính diện tích của hình tròn.