Chuyên đề Hệ thức trong tam giác và giải tam giác - Hình học 10

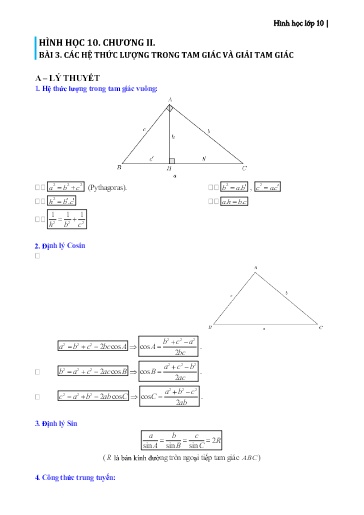
 Hình học lớp 10 | 
 HÌNH HỌC 10. CHƯƠNG II. 
 BÀI 3. CÁC HỆ THỨC LƯỢNG TRONG TAM GIÁC VÀ GIẢI TAM GIÁC 
A – LÝ THUYẾT 
1. Hệ thức lượng trong tam giác vuông: 
 a2 b 2 c 2 (Pythagoras). b2 a. b , c2 a. c 
 h2 b . c a.. h bc 
 1 1 1
 h2 b 2 c 2
2. Định lý Cosin 
 b2 c 2 a 2
 a2 b 2 c 2 2 bc cos A cos A . 
 2bc
 a2 c 2 b 2
 b2 a 2 c 2 2 ac cos B cos B . 
 2ac
 a2 b 2 c 2
 c2 a 2 b 2 2 ab cos C cos C . 
 2ab
3. Định lý Sin 
 a b c
 2R 
 sinABC sin sin
 ( R là bán kính đường tròn ngoại tiếp tam giác ABC ) 
4. Công thức trung tuyến: 
 Hình học lớp 10 | 
 1 1 1 2SSS 2 2
Ta có: S ahS.,.,.,,a bhS b ch c a b c . 
 2 2 2 ha h b h c
 222SSS
 abc h h h 1 1 1
Khi đó: pS a b c . 
 22 ha h b h c
S p p a p b p c 
 111 1112 SSS 1112 1112 
 SSSS 
 hhhabc hhhh abca hhhh abcb hhhh abcc 
 2 111 111111111 
 S 
 hhhabc hhhhhhhhh abcabcabc 
 2
 22122111 222111
 SS222 22 4 22222244 4 
 hhhcab hh ab h c hhhhhhhh acbcabab... h c
 2
 2 1 1 1 1 1 1 1
 SS 2 
 h2 h 2 h 2 h 4 h 4 h 4 2
 a b c a b c 1 1 1 1 1 1 
 2 2 2 2 4 4 4 
 h h h h h h
 a b c a b c 
Chứng minh công thức 4. 
 3
 2 2 2 2 2 2 2 2 2
 2 2 2 2 b c a ma m b m c a b c 
 2 b c a 4
 ma 
 2 4 4 4 4 4 2 2 2 2 2 2
 4 a 4 b 4 c 4 a b 4 a c 8 b c
 2 2 2 m 
 2 2 2 2 a c b a
 2 a c b 16
Ta có: mb 4 4 4 2 2 2 2 2 2 
 2 4 4 4 4a b 4 c 4 a b 8 a c 4 b c
 mb 
 2 2 2 2 a2 b 2 c 2 16
 2 a b c 
 mc 4 4 4 2 2 2 2 2 2
 2 4 4 4 4a 4 b c 8 a b 4 a c 4 b c
 m 
 c 16
 2222 9 444 22 22 22
 mmma b c abc 2 ab 2 bc 2 ac 
 16
 4 4 49 4 4 4
 ma m b m c a b c 
 16
 2222 4449 444222222
 mmma b c 2 mmm a b c abcabbcac 2 2 2 
 16
 44422222216 2222 444
 abcabbcac2 2 2 mmma b c 2 mmm a b c 
 9 
 abc abc abc abc 
Ta có: S p p a p b p c ... 
 2 2 2 2 
 11
 abc abcabcabc abcabccabcab 
 244 
 112 2 2 2 2 2
 abccab 2 2 abcababccab .. 2 4 2 
 44 
 Hình học lớp 10 | 
cos 90 sin cos 180 cos 
tan 90 cot tan 180 tan 
cot 90 tan cot 180 cot 
4. Các giá trị lượng giác của 1 số góc (cung) đặc biệt 
 0 30 45 60 90 180 
 sina 0 1 2 3 1 0 
 2 2 2
 cos a 1 3 2 1 0 1 
 2 2 2
 tan a 0 3 1 3 || 0 
 3
 cot a || 3 
5. Một số hệ thức cơ bản 
 sin x
a) sin22xx cos 1 b) tanxx .cot 1 c) tan x 
 cos x
 cos x 1 1
d) cot x e) 1 tan2 x f) 1 cot2 x 
 sin x cos2 x sin x
II/ TÍCH VÔ HƯỚNG CỦA 2 VECTƠ 
1. Góc giữa 2 vectơ 
* Định nghĩa: 
Cho 2 véc tơ a và b đều khác véc tơ 0 . Từ 1 điểm O bất kỳ ta vẽ OA a và OB b 
Ta có a, b AOB 
* Lưu ý các trường hợp đặc biệt 
a) a, b 90 a  b b) a, b 0 a , b cùng hướng 
 Hình học lớp 10 | 
 1 1 1
a.. h b c 
 h2 b 2 c 2
2/ Định lý côsin 
a2 b 2 c 2 2 bc .cos A b2 a 2 c 2 2 ac .cosB c2 a 2 b 2 2 ab .cosC 
Hệ quả: 
 b22 c a a22 c b a b c2
cos A cosB cosC 
 2bc 2ac 2ab
3/ Công thức tính độ dài đường trung tuyến 
 b2 c 2 a 2 a2 c 2 b 2 a2 b 2 c 2
m2 m2 m2 
 a 24 b 24 c 24
4/ Định lý sin 
Trong tam giác ABC, R là bán kính đường tròn ngoại tiếp tam giác; ta có 
 a b c
 2R 
sinA sinB sin C
5/ Các công thức tính diện tích tam giác 
 1 1 1
S a... h b h c h 
 2a 2 b 2 c
 1 1 1
S absin C bc sin A acs inB 
 2 2 2
 abc
S (R là bán kính đường tròn ngoại tiếp tam giác) 
 4R
S pr (r là bán kính đường tròn nội tiếp tam giác) 
S p p a p b p c (công thức Hê rông) 
IV. HỆ THỐNG BÀI TẬP TỰ LUẬN 
 DẠNG 1: MỘT SỐ BÀI TOÁN GIẢI TAM GIÁC, TÍNH CẠNH, GÓC, 
 CHIỀU CAO, DIỆN TÍCH 
 Ví dụ 1 
 Cho tam giác có , và độ dài đường trung tuyến . Tính độ dài 
 , chu vi và diện tích . 
 Lời giải 
 Hình học lớp 10 | 
 13a2
* Diện tích tam giác ABC là: S AB. AC .sin A . 
 22
 Ví dụ 4 
 Cho tam giác với ba cạnh . Tính đường cao . 
 Lời giải 
Diện tích: S p( p 13)( p 14)( p 15) 84 . 
 2.S 56
Đường cao cần tìm: h . 
 c 15 5
 Ví dụ 5 
 Cho tam giác có và góc . Tính độ dài đoạn . 
 Lời giải 
Áp dụng định lý Cô-Sin ta có AC AB22 BC 2 AB . BC .cos B 3 13 . 
 Ví dụ 6 
 Cho tam giác có , và diện tích . Tính cạnh 
 Lời giải 
 1 13 B 60
Ta có: S . AB . BC .sin B nên 3 3 .3.4.sinBB sin 
 2
 22 B 120
+) B 60 áp dụng định lí côsin ta có: 
 1
AC2 AB 2 BC 2 2 AB . BC .cos B 9 16 2.3.4. 13 AC 13 . 
 2
+) B 120 áp dụng định lí côsin ta có: 
 2 2 2 1
AC AB BC 2 AB . BC .cos B 9 16 2.3.4. 37 AC 37 . 
 2
 Ví dụ 7 
 Cho có . 
 a) Tính . 
 b) Tính diện tích của tam giác ABC. 
 Lời giải 
a) Tính a 
Áp dụng định lý cosin vào ABC ta có: 
a2 b 2 c 2 2 bc cos A 8 2 5 2 2.8.5.cos120 0 129 a 129. 
Tính B