Chuyên đề Hàm số và đồ thị ôn thi vào Lớp 10

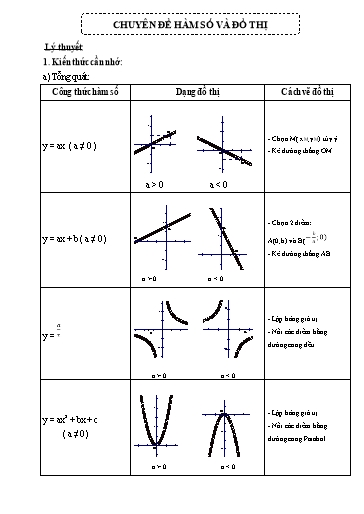
 CHUYÊN ĐỀ HÀM SỐ VÀ ĐỒ THỊ
 Lý thuyết:
 10
 1. Kiến thức cần nhớ: 10
 8
 a) Tổng quát: 8
 6
 Công thức hàm số Dạng đồ thị 6 Cách vẽ đồ thị
 4
 4
 2
 M 2
 - Chọn M( xM;yM) tùy ý.
-15 y = -ax10 ( a ≠ 0 ) -5 O 10 5 10 15
 -15 -10 -5 O -5 Kẻ đường thẳng10 OM 15
 10
 -2 M
 8
 -2
 8
 -4
 a > 0 6 a < 0
 -4
 6
 -6
 4
 -6
 4
 -8
 2
 -8 - Chọn 2 điểm:
 A A
 2
 y = ax + b ( a ≠ 0) B -10
 -15 -10 -5 5 -10 10 A(0;b) và B(15
 8
 B - Kẻ đường thẳng AB
 -15 -10 8 -5 5 10 15
 -2
 6
 -2
 6
 a > 0 - 4 a < 0
 4
 -4
 4
 -6
 2
 2 -6
 -8 - Lập bảng giá trị
 -8 10
 -10 -5 -10 A -5 5 A 10 - Nối5 các điểm bằng 10
 y = -10
 8 đường cong đều
 -2 -10
 -2
 10
 6
 -4
 8 -4
 a > 0 a < 0
 4
 -6
 6 -6
 2
 -8
 4
 O -8 - Lập bảng giá trị 
 y = ax2 + bx-15 + c -10 -5 5 10 15
 2 - Nối các điểm bằng 
 ( a ≠ 0) -2
 đường cong Parabol 
 -15 -10 -5 O 5 -4 10 15
 -2
 a > 0 -6a < 0
 -4 -8
 -6 -10
 -8
 -10  Dạng 3: Lập phương trình hàm số biết một số điều kiện:
 • Lập phương trình đường thẳng (d) biết d di qua 2 điểm A(xA; yA) và B(xB;yB)
Cách làm: Giả sử đường thẳng (d) có dạng: y = ax + b ( * )
Vì (d) đi qua A và B nên ta có hệ phương trình: 
Giải hệ phương trình này ta được a và b sau đó thay vào (*) ta được phương trình đường 
thẳng cần tìm.
 • Lập phương trình đường thẳng (d) đi qua A(xA; yA) và biết hệ số góc là k.
Cách làm: Giải phương trình : yA = kxA + b ta tìm được b.
 • Lập phương trình bậc hai biết 2 nghiệm là x1 và x2:
Cách làm: Có 2 cách làm
+ Cách 1: Phương trình có 2 nghiệm là x1 và x2 là: a( x- x1).(x – x2) = 0
 ( Nếu bài yêu cầu 1 phương trình thì chọn a = 1)
+ Cách 2: Áp dụng hệ thức Vi – ét: Ta tính 
 2
Khi đó x1 và x2 là nghiệm của phương trình: x - Sx + P = 0
 Dạng 4: Tổng hợp 
 Bài tập có chứa tham số m. Tìm m để bài tập thỏa mãn một số điều kiện nào đó
Cách làm : Vận dụng tất cả các kiến thức ở dạng 1, 2 và 3. 
C. Bài tập áp dụng:
Bài 1: 1. Hãy lập một phương trình có 2 nghiệm là ?
 2. Cho Parabol (P) có phương trình: y = x2 và đường thẳng (d) có phương trình : 
y = mx + m + 3. Tìm m để (P) và (d) cắt nhau tại hai điểm ở bên phải trục tung?
Bài 2: Cho Parabol ( P ) có phương trình: y = - x2 và đường thẳng (d) có phương trình : 
y = - mx + m - 1. Tìm m để (P) và (d) cắt nhau tại hai điểm phân biệt có hoành độ là x1
và x2 thỏa mãn: ?
Bài 3: Cho đường thẳng d1 : y = ( m+1)x +2 và đường thẳng d2 : y = 2x + 1.
 1. Xác định tọa độ giao điểm của 2 đường thẳng trên theo m?
 2. Tìm m sao cho d1 và d2 cắt nhau tại một điểm mà hoành độ và tung độ của điểm 
 đó trái dấu? 2
y = - x tại hai điểm phân biệt A ( x1;y1) và B(x2; y2)
 2) Tìm m sao cho: = - 4
Bài 15: Cho parabol (P): y = x2 và đường thẳng (d): y = x - m+1.Tìm m để (d) cắt (P) tại 
2 điểm phân biệt nằm ở hai phía của trục tung.
Bài 16: Cho hàm số có đồ thị là đường parabol P, đường thẳng có hệ số góc 
k đi qua điểm ( 0; -2) 
 a) Viết phương trình đường thẳng d
 b) Chứng minh rằng khi k thay đổi, (d) luôn cắt ( P) tại 2 điểm phân biệt.
Bài 17: Cho parabol (P): y = x2 và đường thẳng (d): y = - mx - m+1.Tìm m để (d) cắt 
(P) tại 2 điểm phân biệt mà tổng các tung độ của nó nhỏ nhất?
Bài 18: Cho 3 đường thẳng (d1) : y = x + 3; (d2) : y = - x + 1 và (d3) : y = x - m - 2.
Tìm m để 3 đường thẳng trên đồng quy.
Bài 19:Cho Parabol (P) : y = x2 và đường thẳng (d) : y = x + 2.
 1) Chứng minh rằng (d) luôn cắt (P) tại hai điểm phân biệt A và B.
 2) Tính diện tích tam giác OAB.
Bài 20:Cho Parabol (P) : y = x2 và đường thẳng (d) : y = ( 2m + 2)x – m2 – 2m.Tìm m 
để (d) cắt (P) tại hai điểm có hành độ x1 và x2 sao cho: 2x1 + x2 = 5.
Bài 21: Cho các hàm số y = 2x – 2 và y = (m+1)x – m2 – m.( m khác 1)
 1) Vẽ đồ thị các hàm số khi m = -2
 2) Tìm m để đồ thi hai hàm số trên là các đường thẳng song song.
Bài 22: Cho đường thẳng (d): 2(m – 1)x + ( m – 2)y = 2
 1) Vẽ đường thẳng (d) với m = ½
 2) Chứng minh rằng (d) luôn đi qua một điểm cố định với mọi m.
 3) Tìm m để (d) cách gốc tọa độ một khoảng lớn nhất?
Bài 23: Cho (P) : y = mx2 ( m khác 0 ) và (d) : y = 2(m – 2) x – m + 3. Tìm m để (d) cắt 
(P) tại hai điểm phân biệt có hoành độ trái dấu.
Bài 24: Cho (P) : y = x2 ( m khác 0 ) và (d) : y = 2x + m
 1) Vẽ đồ thị hai hàm số trên cùng hệ tọa độ khi m = 3 và tìm tọa độ giao điểm .
 2) Tìm m để (d) tiếp xúc (P), xác định tọa độ giao điểm
Bài 25: Cho (P) : y = - và (d) : y = x + 2 c) Khi m khác 0 , tìm m sao cho khoảng cách từ gốc tọa độ đến (d) bằng 1
Bài 35:Cho (P) : y = x2 và (d) : y = x + 2
 a) Vẽ đồ thị hai hàm số trên cùng hệ Oxy
 b) Gọi A = (d) cắt (P). Tính diện tích tam giác AOB
Bài 36: Cho (P): y = x2 và (d) : y = 2x – m + 1
 a) Tìm m để (d) cắt (P) tại hai điểm phân biệt A và B
 b) Gọi x1 và x2 là hoành độ của A và B. Tìm m sao cho: = 10
Bài 37: Cho (P): y = -x2 và (d) : y = mx – m – 1. Tìm m để (d) cắt (P) tại hai điểm phân 
biệt A và B nằm bên trái trục oy, bên phải trục oy; ở hai phía trục oy?
Bài 38: Cho (d) : y = (m - 2)x + 3 , m ≠ 2 và (d’) : y = -m2x + 1 , m ± 0
 a) Tìm m để (d) // (d’)
 b) Tìm m để (d) cắt Ox tại A, cắt Oy tại B mà 
Bài 39: Cho (d) : y = ( 2m + 1)x – 2 , ( m ≠ cắt Ox tại A, cắt Oy tại B. 
Tìm m sao cho:
 a) Khoảng cách từ O (gốc tọa độ) đến (d) bằng 
 b) S▲AOB = 
Bài 40: Cho (P) : y = - x2 và (d) : y = 2mx – 2m + 1. Tìm m để (d) cắt (P) tại hai điểm 
phân biệt có hoành độ x1 và x2 thỏa mãn: 
 a) x2 = 3x1 ?
 b)
 c) x2 , x1 trái dấu ( cùng dấu, cùng âm, cùng dương )
Bài 41: Cho (P) : y = và (d) : y = mx + 2. Tìm m sao cho (d) cắt (P) tại hai điểm 
phân biệt có hoành độ x1,x2 thỏa mãn : nhỏ nhất.
Bài 42: Cho (P) : y = và (d) đi qua I(0;2) có hệ số góc k.
 a) Chứng minh rằng (d) luôn cắt (P) tại hai điểm phân biệt A và B
 b) Gọi H và K lần lượt là hình chiếu vuông góc của A và B trên Ox. 
 Chứng minh tam giác IHK vuông tại I?