Chuyên đề Hàm số bậc hai - Toán Lớp 10 Sách Kết nối tri thức

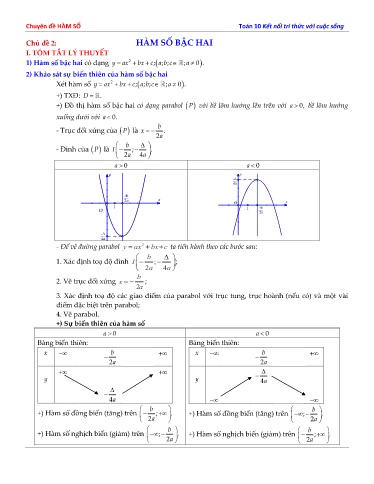
 Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống 
Chủ đề 2: HÀM SỐ BẬC HAI 
I. TÓM TẮT LÝ THUYẾT 
1) Hàm số bậc hai có dạng y ax2 bx c; a ; b ; c ; a 0 . 
2) Khảo sát sự biến thiên của hàm số bậc hai 
 Xét hàm số y ax2 bx c; a ; b ; c ; a 0 . 
 +) TXĐ: D . 
 +) Đồ thị hàm số bậc hai có dạng parabol P với bề lõm hướng lên trên với a 0, bề lõm hướng 
 xuống dưới với a 0. 
 b
 - Trục đối xứng của là x . 
 2a
 b 
 - Đỉnh của là I ;. 
 24aa
 a 0 a 0 
 y y
 __-Δ
 4a
 __-b
 2a x
 O x
 1 1 __-b
 O 2a
 -Δ
 __ 
 4a 
 - Để vẽ đường parabol y ax2 bx c ta tiến hành theo các bước sau: 
 b 
 1. Xác định toạ độ đỉnh I ; ; 
 24aa
 b
 2. Vẽ trục đối xứng x ; 
 2a
 3. Xác định toạ độ các giao điểm của parabol với trục tung, trục hoành (nếu có) và một vài 
 điểm đặc biệt trên parabol; 
 4. Vẽ parabol. 
 +) Sự biến thiên của hàm số 
 Bảng biến thiên: Bảng biến thiên: 
 x b 
 2a
 y 
 4a 
 b
 +) Hàm số đồng biến (tăng) trên ;. +) Hàm số đồng biến (tăng) trên 
 2a
 b
 +) Hàm số nghịch biến (giảm) trên ;. +) Hàm số nghịch biến (giảm) trên 
 2a
 Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống 
 a) Đi qua ba điểm ABC 0;1, 1;1, 1;1 ; 
 b) Đi qua điểm D 3;0 và có đỉnh là I 1;4 ; 
 c) Đi qua A 8;0 và có đỉnh I 6;12 ; 
 d) Đạt GTNN bằng 4 tại x 2 và đi qua A 0;6 ; 
Câu 10: Cho hàm số y x2 23 x có đồ thị P . 
 a) Lập bảng biến thiên và vẽ đồ thị 
 b) Dựa vào đồ thị P , biện luận số nghiệm của phương trình x2 2 x 2 m 0. 
 c) Tìm m để phương trình x2 2 x 3 m 1 có 4 nghiệm phân biệt. 
 d) Tìm để phương trình x2 2 x 2 m 0 có 4 nghiệm phân biệt. 
 2
 e) Tìm để phương trình f x m 10 f x m có 8 nghiệm phân biệt. 
 2
Câu 11: Tìm m để parabol y x2 x cắt đường thẳng ym tại 2 điểm phân biệt. 
Câu 12: Cho parabol P : y x2 2 x m 1. Tìm tất cả các giá trị thực của m để parabol cắt Ox tại 
 hai điểm phân biệt có hoành độ dương. 
Câu 13: Tìm tất cả các giá trị thực của tham số sao cho parabol P :4 y x2 x m cắt tại hai 
 điểm phân biệt AB, thỏa mãn OA 3. OB 
Câu 14: Tìm tất cả các giá trị thực của tham số để đường thẳng d: y mx cắt đồ thị hàm số 
 P : y x32 6 x 9 x tại ba điểm phân biệt. 
Câu 15: Cho parabol P : y x2 4 x 3 và đường thẳng d:3 y mx . Tìm giá trị thực của tham số 
 33
 để d cắt P tại hai điểm phân biệt AB, có hoành độ xx12, thỏa mãn xx12 8 . 
Câu 16: Tìm tất cả các giá trị thực của tham số để phương trình x2 5 x 7 2 m 0 có nghiệm 
 thuộc đoạn 1;5 . 
III. BÀI TẬP TRẮC NGHIỆM 
Câu 17: Trong các hàm số sau hàm số nào là hàm số bậc hai? 
 2xx3 3 5
 A. y 2 x2 3 x 5 B. y . C. y 2 x23 3 x 5 . D. yx 32. 
 x
Câu 18: Điểm nào sau đây không thuộc đồ thị hàm số yx 2 2 ? 
 A. P 2;2 . B. Q 3;3 . C. N 2;2 . D. M 1; 1 .
Câu 19: Đồ thị hàm số y x2 x đi qua điểm nào dưới đây? 
 A. N 2;6 . B. M 1;1 . C. P 2;3 . D. Q 1;1 . 
Câu 20: Cho hàm số y 3 x2 4 x 3 có đồ thị (P). Trục đối xứng của (P) là đường thẳng có phương 
 trình: 
 2 2 4 4
 A. x . B. x . C. x . D. x 
 3 3 3 3
Câu 21: Đỉnh của parabol y x2 45 x có toạ độ là 
 A. 0;2 . B. 1;2 . C. 2;0 . D. 2;1 . 
Câu 22: Tìm để parabol (P ) : y mx2 2 x 3 có trục đối xứng là đường thẳng x 2 . 
 Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống 
 Hàm số đã cho đồng biến trên khoảng nào dưới đây? 
 A. 2; . B. ;2 . C. 3 . D. 1; . 
Câu 33: Cho hàm số y 2 x2 4 x 1. Khẳng định nào sau đây đúng? 
 A. Hàm số đồng biến trên khoảng . B. Hàm số nghịch biến trên khoảng ; . 
 C. Hàm số đồng biến trên khoảng 2; . D. Hàm số nghịch biến trên khoảng . 
Câu 34: Cho hàm số y x2 35 x . Hàm số đã cho đồng biến trên khoảng nào? 
 3 3 3
 A. ;3 . B. ; . C. ; . D. ; . 
 2 2 2
Câu 35: Hàm số nào sau đây đồng biến trên ? 
 A. yx 2 1. B. y x2 x . C. yx 1. D. yx 1. 
Câu 36: Cho hàm số y x2 2 x . Mệnh đề nào sau đây đúng? 
 A. Hàm số đã cho đồng biến trên khoảng 1; . 
 B. Hàm số đã cho nghịch biến trên khoảng 1; . 
 C. Hàm số đã cho đồng biến trên khoảng 
 D. Hàm số đã cho nghịch biến trên khoảng 
Câu 37: Cho hàm số f x x2 2018 x 2020. Khẳng định nào sau đây đúng? 
 11 11 
 A. ff 2019 2018 . B. ff 2019 2018 . 
 22 22 
 1009 1008 1008 1007
 C. ff 22 . D. ff 22 . 
Câu 38: Tìm tất cả giá trị tham số m để hàm số y x2 m 12 x m đồng biến trên 1; . 
 A. m 3 . B. m 3 . C. m 3 . D. m 3 . 
Câu 39: Tìm tất cả các giá trị của tham số để hàm số y x2 2 m 1 x m 2 nghịch biến trên 
 khoảng 1;2 . 
 A. m 1. B. m 1. C. m 0 . D. m 0 . 
Câu 40: Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số 
 y f( x ) m 2 x2 2 mx m 2021 nghịch biến trên khoảng ;3 ? 
 A. 2. B. 1. C. 3. D. 4. 
Câu 41: Có bao nhiêu giá trị nguyên của tham số để hàm số y x2 2 m 1 x 3 nghịch biến trên 
 2 ; ? 
 A. . B. 6 . C. 5 . D. 4 . 
Câu 42: Cho hàm số bậc hai y ax2 bx c có đồ thị như hình vẽ bên dưới: 
 Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống 
Câu 47: Đồ thị hình bên dưới là đồ thị của hàm số bậc hai nào? 
 A. y x2 2. x . B. y x2 2. x C. y x2 2 x 1. D. y x2 2. x 
Câu 48: Đồ thị sau là đồ thị của hàm số nào? 
 A. y x2 23 x . B. y x2 21 x . C. y x2 22 x . D. y x2 21 x . 
Câu 49: Hình bên là đồ thị của hàm số nào sau đây? 
 A. y x2 23 x . B. y x2 23 x . C. . D. y x2 23 x . 
Câu 50: Hàm số y 4 x2 3 x 1 có đồ thị là một trong bốn hình vẽ dưới đây. Đồ thị đó là đồ thị nào? 
 A. . B. . C. . D. . 
Câu 51: Đồ thị hàm số y x2 2 x thể hiện bởi hình vẽ nào dưới đây? 
 A. B. C. D. 
 y y y y
 1
 -1 O 1
 1 2 x
 2 2
 O x -1 O 1 x -1
 O 1 2 x
 -1