Chuyên đề Góc giữa hai mặt phẳng - Hình học 11

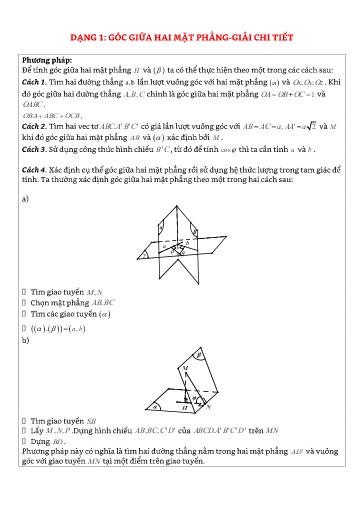
 DẠNG 1: GÓC GIỮA HAI MẶT PHẲNG-GIẢI CHI TIẾT 
Phương pháp: 
Để tính góc giữa hai mặt phẳng H và  ta có thể thực hiện theo một trong các cách sau: 
Cách 1. Tìm hai đường thẳng a,b lần lượt vuông góc với hai mặt phẳng α và Ox,, Oy Oz . Khi 
đó góc giữa hai đường thẳng ABC,, chính là góc giữa hai mặt phẳng OA OB OC 1 và 
OABC . 
OBA ABC OCB . 
Cách 2. Tìm hai vec tơ ABC.''' A B C có giá lần lượt vuông góc với AB AC a, AA ' a 2 và M 
khi đó góc giữa hai mặt phẳng AB và xác định bởi . 
Cách 3. Sử dụng công thức hình chiếu BC' , từ đó để tính cos thì ta cần tính a và b . 
Cách 4. Xác định cụ thể góc giữa hai mặt phẳng rồi sử dụng hệ thức lượng trong tam giác để 
tính. Ta thường xác định góc giữa hai mặt phẳng theo một trong hai cách sau: 
a) 
 α
 β
 a b
 p
 γ q
 Tìm giao tuyến MN, 
 Chọn mặt phẳng AB, BC 
 Tìm các giao tuyến 
  ,, ab 
b) 
 β
 M
 φ
 α H N
 Tìm giao tuyến SB 
 Lấy MNP,,.Dựng hình chiếu AB,,'' BC C D của ABCD.'''' A B C D trên MN 
 Dựng BD . 
Phương pháp này có nghĩa là tìm hai đường thẳng nằm trong hai mặt phẳng AD ' và vuông 
góc với giao tuyến tại một điểm trên giao tuyến. 
 2 2 2
 33a a2 a
 2 2 2 a
 IC ID CD 1
Tam giác CID có cos 4 4 2 . Chọn A. 
 2.IC . ID aa333a2 3
 2. .
 22 2
Câu 4: Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a . Tính cosin của góc giữa một 
mặt bên và một mặt đáy. 
 1 1 1 1
 A. . B. . C. . D. . 
 2 3 3 2
 Hướng dẫn giải:. 
Chọn C. 
Giả sử gọi hình chóp tứ giác đều có tất cả các cạnh đều 
bằng là S. ABCD có đường cao SH . 
Ta có: SCD  ABCD CD. Gọi M là trung điểm CD . 
Dễ chứng minh được SM CD và HM CD 
 SCD ,, ABCD SM HM SMH . 
Từ giả thiết suy ra SCD là tam giác đều cạnh có SM là 
 a 3
đường trung tuyến SM . 
 2
 a
 HM 1
 cos 2 . 
 SM a 33
 2
Câu 5: Cho hình chóp S. ABC có hai mặt bên SAB và SAC vuông góc với mặt phẳng 
 ABC , tam giác ABC vuông cân ở A và có đường cao AH H BC . Gọi O là hình chiếu 
vuông góc của lên SBC . Khẳng định nào sau đây sai ? 
 A. SC ABC . B. O SH . 
 C. SAH  SBC . D. SBC , ABC SBA. 
 Hướng dẫn giải: 
 SAB  ABC 
Ta có SAC  ABC  SA  ABC SA  BC . 
 SAB  SAC SA
BC AH 
  BC  SAH BC  SH . 
BC SA 
Mặt khác, AH BC nên SBC ,, ABC SH AH SHA. 
Chọn D. 
Câu 6: Cho hình chóp có đáy là hình thoi tâm cạnh và có góc BAD 600 . Đường 
 3a
thẳng SO vuông góc với mặt phẳng đáy ABCD và SO . Gọi E là trung điểm BC và F 
 4
là trung điểm BE . Góc giữa hai mặt phẳng SOF và là 
 C. BC tạo với P góc 450 . D. tạo với góc 600 . 
 Hướng dẫn giải: 
Gọi H là hình chiếu vuông góc của C lên mặt 
phẳng . 
Khi đó, AC, P AC , AH CAH 600 và 
 BC,, P BC AH CBH . 
Tam giác AHC vuông tại nên 
 CH a 6
sinCAH CH AC .sin CAH a 2.sin 600 
 AC 2
. 
 a 6
 CH a 2
Tam giác CHB vuông tại nên sin 2 450 . 
 BC 2 2
 aa2 2 
Chọn C. 
Câu 10: Cho hình chóp S. ABC có SA ABC và đáy ABC vuông ở A . Khẳng định nào sau 
đây sai ? 
 A. SAB  ABC . 
 B. SAB  SAC . 
 C. Vẽ AH BC, H BC góc AHS là góc giữa hai mặt phẳng SBC và ABC . 
 D. Góc giữa hai mặt phẳng và SAC là góc SCB . 
 Hướng dẫn giải: 
Chọn D. 
Ta có: SA ABC SAB ABC nên đáp án A đúng. 
AB AC, AB  SA AB  SAC  SAB SAC . Nên đáp án 
B đúng 
AH BC; BC  SA BC  SAH 
 SH  BC SBC , ABC SHA . 
Nên đáp án C đúng. 
Ta có: SBC  SAC SC nên đáp án D sai. 
Câu 11: Cho tứ diện ABCD có AC AD và BC BD . Gọi I là trung điểm của CD . Khẳng 
định nào sau đây sai ? 
 A. Góc giữa hai mặt phẳng ACD và BCD là góc AIB . 
 B. BCD  AIB . 
 C. Góc giữa hai mặt phẳng và ABD là góc 
 CBD . 
 D. ACD  AIB . 
 Hướng dẫn giải: 
Chọn C. 
 3 3 6
 A. . B. . C. . D. 6 . 
 2 2 6
 Hướng dẫn giải: 
Chọn D. 
Gọi M là trung điểm của CD . 
 CD OM
Khi đó 
 CD SO
 CD  SM SCD , ABCD SMO . 
Ta có: R OA a AC 22 a AB AD a . 
 a2 SO
 OM tan 6 . 
 2 OM
Câu 15: Cho hình chóp tam giác đều S.ABC với SA= 2AB. Góc giữa SAB và ABC bằng . 
Chọn khẳng định đúng trong các khẳng định sau? 
 1
 A. 600 . B. cos . 
 35
 1 1
 C. cos . D. cos . 
 45 25
 Hướng dẫn giải: C 
Gọi O là tâm của tam giác đều ABC 
Gọi CO AB H suy ra H là trung điểm AB( vì ABC
đều) 
 1 1AB 3 AB 3
 OH AB và OH CH . 
 3 3 2 6
Tìm góc giữa và 
 SAB  ABC AB
 OH AB 
 SO AB SO ( ABC ) 
 SH AB (1) 
Ta có 
 SAB  ABC AB
 OH AB, OH ( ABC ) 
 SH AB, SH ( SAB ) 
 (SAB );( ABC ) SH ; OH SHO 
 2
 22 2 AB 15
Từ (1) suy ra SH SA AH 2 AB AB 
 22
 HK a 23
tan . 
 SH a 3 3
 2
Vậy chọn đáp án B . 
Câu 18: Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật tâm O và khoảng cách từ A 
 2a
đến BD bằng . Biết SA ABCD và SA 2 a . Gọi là góc giữa hai mặt phẳng ABCD và 
 5
 SBD . Khẳng định nào sau đây sai? 
 A. SAB  SAD . B. SAC  ABCD . C. tan 5 . D. SOA . 
 Hướng dẫn giải: 
Chọn D. 
Gọi AK là khoảng cách từ đến 
 2a
Khi đó AK và BD AK , BD SA 
 5
 SA
 SBD , ABCD SK A tan 5. 
 AK
Vậy đáp án D sai. 
Câu 19: Cho hình lăng trụ ABCD. A B C D có đáy là hình thoi, AC 2 a . Các cạnh bên 
vuông góc với đáy và AA a . Khẳng định nào sau đây sai ? 
 A. Các mặt bên của hình lăng trụ là các hình chữ nhật. 
 B. Góc giữa hai mặt phẳng AA C C và BB D D có số đo bằng 60. 
 C. Hai mặt bên AA C và BB D vuông góc 
 với hai đáy. 
 D. Hai hai mặt bên AA B B và AA D D 
 bằng nhau. 
 Hướng dẫn giải: 
Chọn B. 
Ta có: các cạnh bên vuông góc với đáy, đáy là 
hình thoi nên 
Các mặt bên của hình lăng trụ là các hình chữ 
nhật. 
Hai mặt bên và vuông góc với hai đáy. 
Hai hai mặt bên và bằng nhau. 
suy ra đáp án A,C,D đúng. 
Mặt khác hai đáy và ABCD là các hình thoi nên AA C C  BB D D . Suy ra đáp án 
B sai.