Chuyên đề Giải bài toán cực trị liên quan tới mặt phẳng - Hình học 12

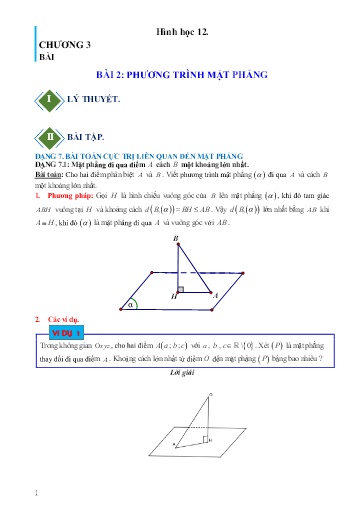
 Hình học 12. 
 CHƯƠNG 3 
 BÀI 
 BÀI 2: PHƯƠNG TRÌNH MẶT PHẲNG 
 I LÝ THUYẾT. 
 = 
 II BÀI TẬP. 
 = 
DẠNG 7. BÀI TOÁN CỰC TRỊ LIÊN QUAN ĐẾN MẶT PHẲNG 
DẠNG 7.1: Mặt phẳng đi qua điểm A cách B một khoảng lớn nhất. 
Bài toán: Cho hai điểm phân biệt và . Viết phương trình mặt phẳng đi qua và cách 
một khoảng lớn nhất. 
1. Phương pháp: Gọi H là hình chiếu vuông góc của lên mặt phẳng , khi đó tam giác 
ABH vuông tại và khoảng cách d B, BH AB . Vậy dB , lớn nhất bằng AB khi 
AH , khi đó là mặt phẳng đi qua và vuông góc với . 
 B
 H A
 α
2. Các ví dụ. 
 Ví DỤ 1 
 Trong không gian Oxyz , cho hai điểm A a;; b c với a , b , c \0  . Xét P là mặt phẳng 
 thay đổi đi qua điểm . Khoảng cách lớn nhất từ điểm O đến mặt phẳng bằng bao nhiêu ? 
 Lời giải 
1 
 Trong không gian Oxyz , cho hai điểm M 0 ; 1; 2 và N 1;1; 3 . Viết phương trình mặt 
 phẳng P đi qua hai điểm M , N sao cho khoảng cách từ điểm K 0 ; 0 ; 2 đến mặt phẳng 
 là lớn nhất. 
 Lời giải 
Mp có dạng AxBy 1 Cz 2 0 AxByCzB 2 C 0 . 
NPABCBCABC 1;1; 3 3 2 0 2 . 
 P : 2 B C x By Cz B 2 C 0. 
 B
Khi đó d K, P . 
 4B22 2 C 4 BC
+ Nếu B 0 thì d K,0 P (loại). 
 11
+ Nếu B 0 thì d K, P . 
 2
 C 2
 2 1 2
 B
Dấu "" xảy ra khi BC . 
Chọn BC 1, 1 ta có phương trình mặt phẳng P : x y z 3 0. 
DẠNG 7.2: Mặt phẳng đi qua điểm M, cắt tia Ox, Oy, Oz tại các điểm A, B, C và liên quan đến 
thể tích. 
1. Phương pháp: 
  Viết phương trình mặt phẳng đi qua M, cắt tia Ox, Oy, Oz tại các điểm A, B ,C. 
  Sử dụng BĐT AM-GM để tìm giá trị nhỏ nhất của thể tích tứ diện OABC. 
2. Các ví dụ: 
 Ví DỤ 5 
 Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm Aa ;0;0 , Bb 0; ;0 , Cc 0;0; , trong 
 đó a 0, b 0, c 0. Viết phương trình mặt phẳng ABC đi qua điểm I 1;2;3 sao cho thể 
 tích khối tứ diện OABC đạt giá trị nhỏ nhất. 
 Lời giải 
 x y z 1 2 3
 Ta có ABC :1 . Do I ABC 1. 
 a b c abc
 1 2 3 6 1
 Ta có 1 33 abc 162. Suy ra V abc 27 . 
 a b c abc OABC 6
 1 1 2 3
 Dấu bằng xảy ra khi a 3; b 6; c 9 . 
 3 abc
 x y z
 Vậy ABC :1 . 
 3 6 9
 Ví DỤ 6 
3 
 x y z 1 1 1
Khi đó mặt phẳng P có dạng 1. Vì đi qua M nên 1. 
 a b c abc
 31 2b
Mặt khác OA 2 OB nên ab 2 nên 1 36 c . 
 2bc 23b 
 11
Thể tích khối tứ diện OABC là V abc b2 c . 
 63
 3 1 3 3 1 9 9116bc2 bc2 81
Ta có 33 3 27 . 
 2b c 4 b 4 b c 16 b2 c 16bc2 3 9 3 16
 9
 a 
 2
 81 3 1 1 9
Vmin khi b . 
 16 43bc 4
 c 3
 Ví DỤ 9 
 Trong không gian với hệ tọa độ Oxyz , cho hình hộp chữ nhật ABCD. A B C D có A trùng với 
 gốc tọa độ O , các đỉnh Bm ;0;0 , Dm 0; ;0 , An 0;0; với m , n 0 và mn 4. Gọi là 
 trung điểm của cạnh CC . Khi đó thể tích tứ diện BDA M đạt giá trị lớn nhất bằng bao nhiêu? 
 Lời giải 
 An 0;0; D 
 B C 
 A
 O
 M Dm 0; ;0 
 Bm ;0;0 C
Cách 1: Ta chia khối hộp chữ nhật ABCD. A B C D thành các hình chóp có thể tích VVM.1 BCD , 
VVBBCA.2 , VVA .3 BC M , VVA .4 MDC , VVDADC.5 , VVA .6 ABD và VVBDA M 7 . Khi đó, ta có: 
 1n 1 1
VV mnVVVVVVV2. . Trong đó V .. m2 V ; 
 ABCD. A B C D 1 2 3 4 5 6 7 1 3 2 2 12
 1 1 1 1 1 1 1 1 1
V n. m2 V ; V m.. m n V ; VV ; VV ; VV . Suy ra 
 2 3 2 6 3 3 4 12 4 12 5 6 6 6
 3 1 1 2
V VVVVVVVVVV V mn ; do m n 44 n m 
 BDA M 7 1 2 3 4 5 6 444
 112 2 3
VBDA M V7 m 44 m m m . 
 44
5 
 Trong không gian với hệ tọa độ Oxyz , viết phương trình mặt phẳng P đi qua điểm M 1;2;3 và 
 cắt các trục Ox , Oy , Oz lần lượt tại ba điểm A , B , C khác với gốc tọa độ O sao cho biểu thức 
 1 1 1
 có giá trị nhỏ nhất. 
 OA2 OB 2 OC 2
 Lời giải 
Cách 1: 
Gọi H là hình chiếu vuông góc của trên mặt phẳng ABC OH ABC . 
 1 1 1 1 1
Ta có: . Dấu “=” xảy ra khi và chi khi HM . 
 OA2 OB 2 OC 2 OH 2 OM 2
 1 1 1 1
Do đó: 2 2 2 2 khi P đi qua điểm M 1; 2; 3 có VTPT OM 1;2;3 
 OA OB OCmin OM
Vậy có phương trình: P : x 2 y 3 z 14 0. 
Cách 2: 
Giả sử Aa ; 0; 0 , Bb 0; ; 0 , Cc 0; 0; với abc. . 0. 
 x y z
Phương trình mặt phẳng : 1. 
 a b c
 1 2 3
Vì đi qua điểm nên ta có phương trình 1 1 . 
 abc
 1 1 1 1 1 1
Ta có: . 
 OA2 OB 2 OC 2 a 2 b 2 c 2
 1 2 32 2 2 1 1 1
Theo bất đẳng thức Bunhiakopxki ta có: 1 1 2 3 2 2 2 . 
 a b c a b c
 1 1 1 14
suy ra , dấu "" xảy ra khi a 23 b c 2 . 
 abc2 2 2 14
 a 14
Từ và suy ra b 7 . 
 14
 c 
 3
Vậy phương trình mặt phẳng cần tìm là: x 2 y 3 z 14 0 . 
DẠNG 7.3: Mặt phẳng cắt mặt cầu S tạo thành đường tròn có bán kính lớn nhất hoặc 
nhỏ nhất. 
 1. Phương pháp 
 Mặt phẳng cắt mặt cầu tạo thành đường tròn có bán kính lớn nhất. 
 Xác định tâm I và bán kính R của mặt cầu . 
 Mặt phẳng cắt mặt cầu theo một đường tròn có bán kính lớn nhất thì mặt phẳng 
 đi qua tâm của mặt cầu. 
 Mặt phẳng cắt mặt cầu tạo thành đường tròn có bán kính nhỏ nhất. 
 Xác định tâm và bán kính của mặt cầu . 
7 
Khi đó: P đi qua A 1;2;3 , có VTPT là IA 1;0;2 nên có phương trình: 
1 x 1 0 y 2 2 z 3 0 xz 2 7 0. 
 Ví DỤ 15 
 Trong không gian với hệ tọa độ Oxyz , cho hai điểm AB 3; 2;6, 0;1;0 và mặt cầu 
 S : x 1 2 y 2 2 z 3 2 25 . Mặt phẳng P : ax by cz 2 0 đi qua AB, và cắt S 
 theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính T a b c . 
 Lời giải 
Mặt cầu có tâm I 1;2;3 và bán kính R 5. 
 AP 3abc 2 6 2 0 ac 22
Ta có 
 BP b 20 b 2
 22
 2
Bán kính của đường tròn giao tuyến là r R d I; P 25 d I ; P 
Bán kính của đường tròn giao tuyến nhỏ nhất khi và chỉ khi d I; P lớn nhất 
 a 2 b 3 c 2 2 2cc 4 3 2 c 4 2
Ta có d I, P 2 
 abc2 2 2 2 2cc 2 222 5cc 8 8
 2
 c 4 48cc2 144 192
Xét fc fc 
 5cc2 8 8 2
 2 2 c 4 
 5cc 8 8 2
 5cc 8 8
 c 1
 fc 0 
 c 4
Bảng biến thiên 
 x 4 1 
 y ' 0 0 
 1
 y 5 
 5
 0 1
 5
Vậy lớn nhất bằng 5 khi và chỉ khi c 1 a 0, b 2 a b c 3. 
 Ví DỤ 16 
9