Chuyên đề Giá trị lượng giác của một cung - Đại số 10

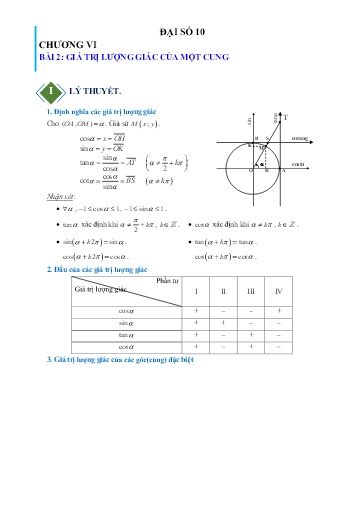
 ĐẠI SỐ 10 
CHƯƠNG VI 
BÀI 2: GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT CUNG 
 I LÝ THUYẾT. 
 = 
 1. Định nghĩa các giá trị lượng giác 
 = T 
 tang
 Cho (,)OA OM . Giả sử M x; y . sin
 = 
 I cos x OH B S cotang 
 K 
 M 
 sin y OK 
 sin 
 tan AT k  cosin 
 cos 2 O H A 
 cos 
 cot BS k 
 sin 
 Nhận xét: 
  , 1 cos 1, 1 sin 1. 
 tan xác định khi k , k . cot xác định khi k , k . 
 2
 sin k 2 sin . tan k tan . 
 cos k 2 cos . cot k cot . 
 2. Dấu của các giá trị lượng giác 
 Phần tư 
 Giá trị lượng giác I II III IV 
 cos + – – + 
 sin + + – – 
 tan + – + – 
 cot + – + – 
 3. Giá trị lượng giác của các góc(cung) đặc biệt 
 sin22 cos 1. tan  cot 1. 
 1 1
 1 tan2 . 1 cot2 . 
 cos2 sin2 
5. Giá trị lượng giác của các góc có liên quan đặc biệt 
a. Hai góc đối nhau: 
 cos cos 
 sin sin 
 tan tan 
 cot cot 
b. Hai góc bù nhau: 
 cos cos 
 sin sin 
 tan tan 
 cot cot 
c. Hai góc phụ nhau: 
 cos sin 
 2
 sin cos 
 2
 tan cot 
 2
 cot tan 
 2
d. Hai góc hơn kém : 
 cos cos 
 sin sin 
 tan tan 
 cot cot 
 2 DẠNG TOÁN XÉT DẤU GIÁ TRỊ LƯỢNG GIÁC 
 = 
 Ví dụ 1 
 Cho góc thỏa điềuVí ki ệ n 0 . Xét dấu của các giá trị lượng giác sau 
 2
 1). sin 
 2). cos 
 2
 3). tan 
 5 
 4). cot 
 2
 Lời giải 
1). Do 0 nên 0 . 
 2 2
Vậy góc nằm trong góc phần tư thứ 4, nên sin 0. 
2). Do 0 nên . 
 2 22
Vậy góc nằm trong góc phần tư thứ 2, nên cos 0 . 
 2 2
3). Do 0 nên . 
 2 2
Vậy góc nằm trong góc phần tư thứ 3, nên tan 0 . 
 55 
4). Do 0 nên 2 . 
 2 22
 5 5 
Vậy góc nằm trong góc phần tư thứ 1, nên cot 0 . 
 2 2
 Ví dụ 2 
 Cho 0 90 . Xét dấu của các biểu thức sau: 
 Ví 
 a) A sin 90  . 
 b) B cos 45  . 
 c) D cos 2 90  . 
 d) C cos 270  . 
 Lời giải 
 a) 0 90  90  90  180  sin 90  0 . Suy ra A 0 . 
 b) 0 90  45  45  45  cos 45  0 . Suy ra B 0 . 
 c) 0 90  90  2 90  270  cos 2 270  0 . Suy ra D 0 . 
 d) 0 90  180  270  270  cos 270  0. Suy ra C 0 . 
 Ví dụ 3 
 Ví 
 3 10 1
 sin tan .cos , cot 10 . 
 10 tan 
 9 16 4
c. Ta có sin22 1 cos 1 sin . 
 25 25 5
 4
Do 0 90  nên sin 0. Suy ra sin . 
 5
 sin 4 13
 Khi đó tan cot . 
 cos 3 tan 4
 1 1 1
d. Ta có 1 cot22 sin 
 sin22 1 cot 5
 5 5
 cos . Mặt khác 270 360  nên sin 0 sin . 
 5 5
 25 1
 cos cot .sin , tan 5 . 
 5 cot 
 Ví dụ 2 
 Ví 
 3 
 a) Cho tan 2 và . Tính giá trị của biểu thức A 3sin 2cos . 
 2
 3sin cos
 b) Cho cot 2. Tính giá trị của biểu thức B . 
 sin cos
 Lời giải 
 113 
a) Ta có: tan22 1 cos . Với cos 0 . 
 cos2 5 2
 1 1 2
Vậy cos sin cos .tan .2 . Do đó 
 5 5 5
 2 1 8
A 3sin 2cos 3. 2 
 5 5 5
 cos 
b) Ta có cot 2 2 cos 2sin thay vào biểu thức ta được:
 sin 
 3sin cos 3sin 2sin 5sin 
B 5.
 sin cos sin 2sin sin 
 Ví dụ 3 
 Ví 
 3
 a) Cho cosxx sin . Tính giá trị biểu thức A sinxx cos . 
 4
 6
 b) Cho cosxx 2sin . Tính sin x , cos x 
 5
 c) Cho tanaa cot 2; tan a , cot a mang dấu âm. Tính giá trị biểu thức C tanaa cot . 
 d) Cho 2tanaa 3cot 1. Tính giá trị biểu thức D tan a cot a . 
 Lời giải 
 2
 3 2 3 22 9
a) cosxx sin cosxx sin cosx sin x 2sin x .cos x . 
 4 4 16
 3
 b) B sin2 sin 2 c os 2 x 
 88
 5 
 c) C sin x c os x tan x tan x 
 2 2 2 
 Lời giải 
 22 
a) A sin x sin x cos x sin x 
 22 
 22 
 A sin x cos x cos x sin x 
 2 
 1 sinxx sin 1.
 3
b) B sin2 sin 2 cos 2 x 
 88
 33 
 Vì sin cos
 8 8 2 8 8 
 B sin2 cos 2 c os 2 x 1 c os 2 x sin 2 x.
 88 
c) 
 5 
C sin x cos x tan x tan x 
 2 2 2
C sin x c os x tan x tan x cos x cos x 0
 2 2 2
 Ví DỤ 2 
 Ví 
 Tính giá trị lượng giá của các biểu thức lượng giác sau: 
 a) A sin2 25 0 sin 2 87 0 sin 2 65 0 sin 2 3 0 . 
 7 5 7 
 b) B sin cos9 tan cot . 
 6 4 2
 Lời giải 
a) Ta có 
sin 250 cos65 0 sin 2 25 0 cos 2 65 0
sin870 cos3 0 sin 2 87 0 cos 2 3 0
 A sin20 25 sin 20 87 sin 20 65 sin 20 3 c os 20 65 c os 20 3 sin 20 65 sin 20 3
 A sin2 65 0 c os 2 65 0 sin 2 3 0 c os 2 3 0 1 1 2
b) Ta có 
A sin cos 4.2 tan cot 3 
 6 4 2 
 15
 A sin cos tan cot 1 1 0 
 6 4 2 2 2
 Ví DỤ 3 
 Ví 
 57 
 Tính giá trị của biểu thức S tan2 tan 2 tan 2 . 
 18 18 18