Chuyên đề Đồng dạng - Bồi dưỡng HSG Toán 8

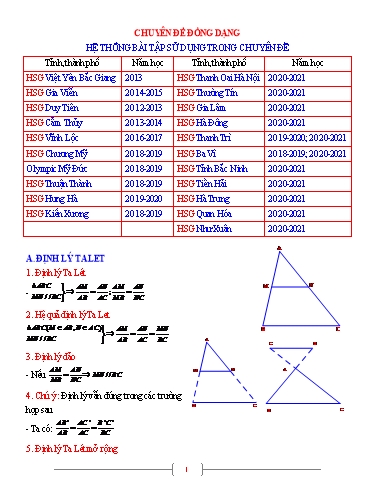
 CHUYÊN ĐỀ ĐỒNG DẠNG
 HỆ THỐNG BÀI TẬP SỬ DỤNG TRONG CHUYÊN ĐỀ
 Tỉnh, thành phố Năm học Tỉnh, thành phố Năm học
HSG Việt Yên Bắc Giang 2013 HSG Thanh Oai Hà Nội 2020-2021
HSG Gia Viễn 2014-2015 HSG Thường Tín 2020-2021
HSG Duy Tiên 2012-2013 HSG Gia Lâm 2020-2021
HSG Cẩm Thủy 2013-2014 HSG Hà Đông 2020-2021
HSG Vĩnh Lộc 2016-2017 HSG Thanh Trì 2019-2020; 2020-2021
HSG Chương Mỹ 2018-2019 HSG Ba Vì 2018-2019; 2020-2021
Olympic Mỹ Đức 2018-2019 HSG Tỉnh Bắc Ninh 2020-2021
HSG Thuận Thành 2018-2019 HSG Tiền Hải 2020-2021
HSG Hưng Hà 2019-2020 HSG Hà Trung 2020-2021
HSG Kiến Xương 2018-2019 HSG Quan Hóa 2020-2021
 HSG Như Xuân 2020-2021
 A
A. ĐỊNH LÝ TALET
1. Định lý Ta Lét
 ABC  AM AN AM AN M N
-  ; 
 MN / /BC AB AC MB NC
2. Hệ quả định lý Ta Let
 ABC(M AB, N AC) AM AN MN B C
  
 MN / /BC AB AC BC A
  C' B'
3. Định lý đảo
 AM AN M N A
- Nếu MN / /BC
 MB NC
4. Chú ý: Định lý vẫn đúng trong các trường 
 B C
hợp sau B C
 AB ' AC ' B 'C '
- Ta có: 
 AB AC BC
5. Định lý Ta Lét mở rộng
 1 Bài 1: 
Cho hình bình hành ABCD và điểm E thuộc 
 A D
đoạn BD . Gọi M , N lần lượt là giao điểm 
 E
của BC, BD với AE . Qua C kẻ đường thẳng 
 F
 N
song song với BD cắt MN tại F . Chứng 
minh rằng B C M
a. AE 2 EM.EN
 1 1 1
b. 
 AE AM AN
 AM FM
c. 
 AN FN
 Lời giải
 EA EN
a) AE 2 EM.EN 
 EM EA
 EA ED EN
Ta có (Các đường thẳng song song )
 EM EB EA
 1 1 1 AE AE AE
b)  
 AE AM AN AE AM AN
 AE DE AE BE AE AE DE EB
Ta có ; 1
 AM DB AN BD AM AN BD
 1 1 1
Chia cả hai vế cho AE, ta được: 
 AE AM AN
 FE BC 
 FC / /BE 
 FM CM FE BC AN FN CN CN MN
c. Ta có  (1);CF / /ED (2)
 BC AN FM CM NM FE CD AB MA
 AB / /CD 
 CM NM  
 FE FN AN MN FN AM
Từ (1)(2) . . (đpcm).
 FM FE MN MA FM AN
 3 DA ED
a. 
 DB FE
b. HC 2 HA.HE
 1 1 1
c. 
 IH AB CF
 Lời giải
 DA ED EA
a) Ta có 
 DB FE EC
 HC HF HE
b) Ta có 
 HA HB HC
 IH IH IC BI
c) Ta có 1 đpcm
 AB CF BC IC
 Bài 4: 
Cho hình thang ABCD AB / /CD . Gọi M là 
 A B
trung điểm của CD , gọi I là giao điểm của 
 AM với BD, K là giao điểm của BM với 
 K
 E F
 AC , đường thẳng IK cắt AD, BC lần lượt tại I
 E và F . Chứng minh rằng:
a. IK / / AB
 D M C
b. EI IK KF
 Lời giải
 AI AB AB AK
a. IK / /MC
 IM DM MC KC
 IK EI DI KM CF KF
b. Ta có EI IK KF .
 AB AB DB MB CB AB
 5 Bài 6: 
Cho hình thang ABCD AB / /CD, AB CD . 
 A B
 AC cắt BD tại M . Kẻ qua M đường thẳng M
 I K
song song với AB cắt AD, BC lần lượt tại I P E
và K
a. Chứng minh rằng MI MK
 D F Q C
b. Kẻ Bx / / AD , Bx cắt AC,CD tại E, F
Kẻ Ay / /BC , Ay cắt BD,CD tại P,Q . Chứng 
minh rằng DE / /IK
c. Biết AB a,CD b . Tính IK theo a và b
 Lời giải
 IM AI
a. Xét ADC, IM / /CD (Hệ quả TaLet) (1)
 CD AD
 MK BK
- Tương tự ta có (2) 
 CD DC
 AI BK
Lại có IK / / AB / /CD (TaLet mở rộng ) (3) 
 AD BC
Từ (1)(2)(3) IM MK 
 BE BP
b. Ta đi chứng minh PE / /DF
 FE PD
 BE AB BP AB
Thật vậy (AB / /CF) (4); (AB / /DQ) (5)
 FE FC PD DQ
 ABFD; ABCQ là các hình bình hành AB DF CQ DQ CF(6) 
 BE PB AB AB
Từ (4)(5)(6) ( ) PE / DF (Ta Lét đảo )
 FE PD FC DQ
c. Ta có IK 2MI 2MK
 MK BM
Xét BCD(MK / /CD) (He.qua.TaLet) (1) 
 CD BD
 MB AB a
Xét MCD(AB / /CD) (He.qua.TaLet) (1) 
 MD CD b
 7 DI DE AD
 DI.BK AB.AD (không đổi)
 AB EB BK
 Bài 8: 
Cho tứ giác ABCD , đường thẳng qua A A B
song song với BC cắt BD ở E . Đường 
 O
thẳng qua B song song với AD cắt AC ở G
a. Chứng minh rằng EG / /CD E G
b. Giả sử AB / /CD . Chứng minh rằng: 
 D C
 AB2 CD.EG
 Lời giải
 OE OG
a) Hướng dẫn EG / /CD  
 OD OC
 OE OA 
 AE / /BC 
 OB OC OE OG
  EG / /CD (TaLet đảo )
 OB OG OD OC
BG / / AB 
 OD OA  
 AB2 AB AB OA OB OG
b. Hướng dẫn AB2 CD.EG  1 . 1 . (BG / / AD)
 CD.EG GE CD OG OD OA
 AB OA OA OD CD OD
Giải: AB / /EG (1); AD / /BD (2); AB / /CD (3)
 EG OG OG OB AB OB
 AB OA OD CD
Từ (1)(2)(3) AB2 CD.EG
 EG OG OB AB
 Bài 9: HSG Thường Tín, năm học 2020 - 2021
Cho hình thang ABCD ( AB//CD và CD AB ). Gọi trung điểm các đường chéo AC và BD 
lần lượt là P và Q . Gọi trung điểm của AB, BC,CD và DA lần lượt là R, N, S và M .
a) Chứng minh rằng RQSP là hình bình hành. Các cạnh bên AD và BC của hình thang 
 ABCD phải có thêm điều kiện gì để RQSP là hình chữ nhật, hình thoi, hình vuông?
 CD AB
b) Chứng minh rằng PQ//AB và PQ .
 2
 9 b) MN là đường trung bình của hình thang ABCD MN // AB
MP là đường trung bình của BAD MP // AB 
 NQ là đường trung bình của BAC NQ // AB 
Theo tiên đề Ơ-clit thì 4 điểm R, N, S, M thẳng hàng ..
 PQ // AB.
 AB CD
Ta có MN ( MN là đường trung bình của hình thang ABCD )
 2
 AB
MP ( MP là đường trung bình của BAD )
 2
 AB
 NQ ( NQ là đường trung bình của BAC )
 2
 AB CD AB AB CD AB
 PQ MN MP NQ .
 2 2 2 2
c) Gọi giao điểm của đường thẳng d với BC và AC lần lượt là F và H 
Vì d // MN// AB EF //AB; HG // AB 
Áp dụng hệ quả định lý Talet vào các tam giác BAD và CAB ta có:
 DE EF CG HG
 (1); (2); AB.CG BC.HG (3)
 AD AB CB AB
 CG CH DE
Tương tự vì d // AB// CD. Áp dụng hệ quả định lý Talet (4)
 CB CA DA
 HG EF
Từ 1 , 2 , 4 suy ra HG EF
 AB AB
 BG FG
Lại có BG.CD BC.FG (5)
 BC CD
Từ 3 , 5 suy ra AB.CG CD.BG BC.HG BC.FG
 AB.CG CD.BG BC(HG FG)
 AB.CG CD.BG BC(HG FH HG)
 AB.CG CD.BG BC(EF FH HG)
 AB.CG CD.BG BC.EG.
d) Do EG// AB// CD. Áp dụng hệ quả định lý Talet vào CAD ta có: 
 11 D· AN M· AD 900 M· AN 900 (2)
Từ (1) và (2) AMN vuôngcân
 ED DN
 2) END có AB//CD (hệ quả talet) (3)
 EA AB
 FM BM
 BFM có BM // AD (hệ quả talet) (4)
 FA DA
Mà DN BM (gt) ; DN BM gt và AB AD (cạnh hình vuông ABCD)
 ED FM
Nên từ (3) và (4), ta có: 
 EA FA
 ED FM
Xét ADM có: E AD, F AM . Mà (cmt)
 EA FA
Nên : EF // DM (talet đảo)
3) Chứng minh được SJAB SJDC SJBC SJAD
SJAB SJDH SJHC SJEA SJED SJBC (1)
Mà Q là trung điểm của BE . Chứng minh được SJAB SJEA
P là trung điểm của BH . Chứng minh được SJHC SJBC (2)
Từ (1) và (2), ta có: SJDH SJED
Mà E và H nằm trên hai nửa mặt phẳng bờ JD .
Gọi EH giao với JD là I ' , h1,h2 là khoảng cách từ E và H đến JD
Vì SJDH SJED nên h1 h2
Từ đó chứng minh I ' là trung điểm của EH . Vậy I ' trùng I
Vậy D, I, J thẳng hàng.
 13