Chuyên đề Đại cương về đường thẳng và mặt phẳng (Phần 2) - Hình học Lớp 11

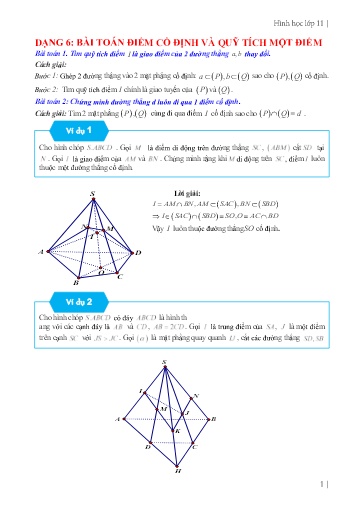
 Hình học lớp 11 | 
DẠNG 6: BÀI TOÁN ĐIỂM CỐ ĐỊNH VÀ QUỸ TÍCH MỘT ĐIỂM 
Bài toán 1. Tìm quỹ tích điểm I là giao điểm của 2 đường thẳng ab, thay đổi. 
Cách giải: 
Bước 1: Ghép 2 đường thẳng vào 2 mặt phẳng cố định: a P , b Q sao cho PQ , cố định. 
Bước 2: Tìm quỹ tích điểm chính là giao tuyến của P và Q . 
Bài toán 2: Chứng minh đường thẳng d luôn đi qua 1 điểm cố định. 
Cách giải: Tìm 2 mặt phẳng PQ , cùng đi qua điểm I cố định sao cho P  Q d . 
 Ví dụ 1 
 Cho hình chóp . Gọi là điểm di động trên đường thẳng , cắt tại 
 . Gọi là giao điểm của và . Chứng minh rằng khi di động trên , điểm luôn 
 thuộc một đường thẳng cố định. 
 S Lời giải: 
 I AM  BN,, AM  SAC BN  SBD 
 I SAC  SBD SO, O AC  BD
 N M Vậy I luôn thuộc đường thẳng SO cố định. 
 I 
 A D
 O
 C 
 B
 Ví dụ 2 
 Cho hình chóp có đáy là hình th 
 ang với các cạnh đáy là và , . Gọi là trung điểm của , là một điểm 
 trên cạnh với . Gọi là mặt phẳng quay quanh , cắt các đường thẳng 
 tại . Tìm tập hợp giao điểm của và . 
 S
 I
 N
 M
 J
 A B
 K
 D C
 H
 1 | Hình học lớp 11 | 
 A
 M
 N
 J
 H
 B F D
 E
 C
 I
a) Ta có EF  P BCD 
 AM AN
 P  MN, BCD BC mà nên MN BC K cố định. 
 AB AC
Vậy EF luôn đi qua điểm K cố định 
b) Ta có 
J ME  NF,,, ME  CMD NF  BDN J CMD  BDN DH H CM  BN 
Giới hạn: 
 ECFBJH  
Khi . Vậy quỹ tích điểm J là đoạn DH. 
 EDFDJD , 
 3 | Hình học lớp 11 | 
 S
 K
 M I E
 A B
 O
 N
 D C
 H
 Lời giải: 
a) Ta có: 
BM SBD 
 SBD  SAC SO, O AC  BD 
SO BM I I BM  SAC 
b) d  AMN SBC 
K AM  SBC , AM  AMN K AMN  SBC d Vì AM, SBC cố định nên K cố 
định. 
Xác định K : 
AM SAD 
 SAD  SBC SH, H AD  BC
SH AM K K AM  SBC .
 Ví dụ 7 
 Cho hai điểm cố định nằm ngoài mặt phẳng cố định sao cho không song song với 
 . là điểm lưu động trong không gian sao cho cắt tại ; cắt tại . 
 Chứng minh đường thẳng đi qua một điểm cố định. 
 Lời giải. 
 5 | Hình học lớp 11 | 
Như vậy: EFM,, cùng nằm trên hai mp P và SCD , do đó ba điểm EFM,, thẳng hàng. Vậy 
đường thẳng EF luôn đi qua một điểm cố định M . 
b). Tương tự, ta có GHM,, cùng nằm trên hai mp Q và SAB ,do đó GHM,, thẳng hàng. Vậy 
các đường thẳng GH luôn đi qua một điểm cố định M . 
 I  AE SAC 
c). Do I SAC  SBD . 
 I  BF SBD 
Tương tự ta cũng có J SAC  SBD ; O SAC  SBD 
Do đó ba điểm IJO,, thẳng hàng. Vậy IJ luôn đi qua điểm cố định O . 
 Ví dụ 9 
 Cho tứ diện . Gọi lần lượt là trung điểm của cạnh là điểm di động 
 trên đoạn . Mặt phẳng cắt tại 
 a). Tứ giác là hình gì ? 
 b). Tìm tập hợp giao điểm của và khi di động trên 
 Lời giải. 
 A
 M Q
 B D
 E P
 N
 C
a). Ta có : MN// AB 
P  MNP ABD 
 MN MNP 
 AB ABD MNP  ABD PQ PQ// MN 
 MN// AB
Vậy tứ giác MNPQ là hình thang. 
b). I  ACD BCD 
Gọi E là trung điểm CD . 
Khi P là điểm di động trên đoạn ED thì PQ MN 
 7 | Hình học lớp 11 | 
 RN// QS // AB
Chứng minh tương tự ta có : 1 
 RN QS AB
 2
Suy ra RNQS là hình bình hành, nên hai đường chéo RS, NQ cắt nhau tại trung điểm của mỗi 
đường. 
Vậy MP,, NQ RS cắt nhau tại trung điểm cuả mỗi đoạn. 
b).Nếu NSQR là hình thoi thì RN RQ 
Mà AB 2 RN . 
 CD 2 RQ
Do đó BA CD là hằng số. 
Vậy điểm A chạy trên đường tròn tâm B có bán kính CD trong mp . 
 Ví dụ 11 
 Câu 5. (VD) Cho hình chóp có điểm là điểm di động trên . 
 a). Xác định giao điểm của và mặt phẳng . 
 b). Tìm tập hợp giao điểm của đường thẳng và 
 Lời giải. 
 S
 M
 I F
 A B
 J
 C
 D
 K 
a). Gọi K AD  BC KM, SC  SBC 
 KM  SC N 
 N SC
 N  KM ADM N SC  ADM 
b). Ta có: I  AN DM 
 I  AN SAC 
 I SAC  SBD 
 I  DM SBD 
 J  AC SAC 
Gọi J AC  BD J SAC  SBD 
 J  BD SBD 
 9 | Hình học lớp 11 | 
 S
 I
 K M
 A C
 J
 B
Trong mặt phẳng IBJ , CM IB K 
K IB, IB  SAB K SAB , đồng thời K CM , suy ra K chính là giao điểm của CM và 
(SAB). 
Nhận thấy K IB , IB cố định. Suy ra điểm K luôn thuộc đường thẳng cố định. 
 Ví dụ 14 
 Cho tứ diện , gọi lần lượt là trung điểm của SA và BC. M là điểm di động trên 
 đoạn IJ, N là điểm di động trên SC sao cho IN cắt (ABC) tại E và MN cắt (ABC) tại điểm F. 
 Chứng minh rằng EF luôn đi qua một điểm cố định khi MN di động. 
 Lời giải: 
 S
 I
 M N
 F
 A C E
 J
 B
Trong mặt phẳng SAC , IN AC E 
E IN, E ABC E là giao điểm của IN và (ABC). 
Trong mặt phẳng IMN , MN JE F 
F MN, M ABC F là giao điểm của MN và (ABC). 
J là trung điểm BC nên J cố định. Vậy EF luôn đi qua điểm J cố định 
 11 | Hình học lớp 11 | 
 Ví dụ 16 
 Cho hình chóp đáy ABCD có AB và CD không song song với nhau. Trên lần 
 lượt lấy hai điểm di động sao cho không song song với . Gọi là giao điểm của 
 AD và BC, giao điểm của SD và A’E, giao điểm của và SC , F là giao điểm của 
 và . Gọi I là trung điểm EF. Hỏi khi di động thì I chạy trên đường cố định nào? 
 Lời giải: 
 S
 F A' B'
 D'
 H
 A C'
 B
 K I
 D
 C
 E
Trong mặt phẳng (ABCD), gọi K là giao điểm của AB và CD. 
Suy ra SK  SAB SCD 
Ta chứng minh F thuộc cả hai mặt phẳng (SAB) và (SCD) nên F thuộc đường thẳng SK cố định. 
 1
Mặt khác I là trung điểm EF nên EI EF , E cố định nên I chính là ảnh của điểm F qua phép vị 
 2
 1
tự tâm I, tỉ số là . 
 2
Gọi H là trung điểm cạnh SE, suy ra H là ảnh của S qua phép vị tự tâm I, tỉ số là . 
Vậy điểm I nằm trên đường thẳng qua H và song song với SK, ta gọi là đường thẳng d 
Kết luận: Khi AB di động thì I chạy trên đường thẳng d cố định với d là đường thẳng đi qua trung 
điểm của cạnh SE và song song với SK cố định. 
 BÀI 2: HAI ĐƯỜNG THẲNG SONG SONG 
 I LÝ THUYẾT. 
 = 
 1) Định nghĩa: Hai đường thẳng được gọi là đồng phẳng nếu chúng cùng nằm trong một 
 mặt phẳng. 
 Hai đường thẳng gọi là chéo nhau nếu chúng không đồng phẳng 
 13 |