Chuyên đề Đa thức - Bồi dưỡng HSG Toán 8

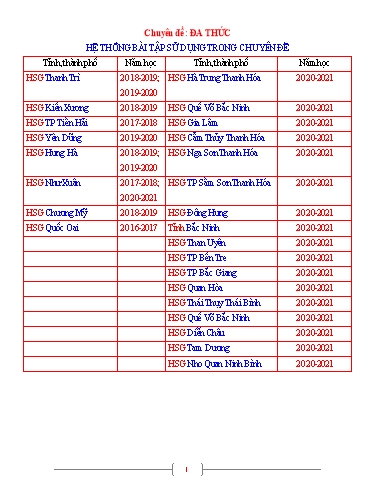
 Chuyên đề : ĐA THỨC
 HỆ THỐNG BÀI TẬP SỬ DỤNG TRONG CHUYÊN ĐỀ
 Tỉnh, thành phố Năm học Tỉnh, thành phố Năm học
HSG Thanh Trì 2018-2019; HSG Hà Trung Thanh Hóa 2020-2021
 2019-2020
HSG Kiến Xương 2018-2019 HSG Quế Võ Bắc Ninh 2020-2021
HSG TP Tiền Hải 2017-2018 HSG Gia Lâm 2020-2021
HSG Yên Dũng 2019-2020 HSG Cẩm Thủy Thanh Hóa 2020-2021
HSG Hưng Hà 2018-2019; HSG Nga Sơn Thanh Hóa 2020-2021
 2019-2020
HSG Như Xuân 2017-2018; HSG TP Sầm Sơn Thanh Hóa 2020-2021
 2020-2021
HSG Chương Mỹ 2018-2019 HSG Đông Hưng 2020-2021
HSG Quốc Oai 2016-2017 Tỉnh Bắc Ninh 2020-2021
 HSG Than Uyên 2020-2021
 HSG TP Bến Tre 2020-2021
 HSG TP Bắc Giang 2020-2021
 HSG Quan Hòa 2020-2021
 HSG Thái Thụy Thái Bình 2020-2021
 HSG Quế Võ Bắc Ninh 2020-2021
 HSG Diễn Châu 2020-2021
 HSG Tam Dương 2020-2021
 HSG Nho Quan Ninh Bình 2020-2021
 1 Dạng 1: Chứng minh một đa thức chia hết cho một đa thức (Xét các đa thức một biến)
Cách 1: Phân tích đa thức bị chia thành nhân tử có một thừa số là đa thức chia
 f (x)g(x)
Nếu f (x) g(x).h(x) 
 f (x)h(x)
 Bài 1: Chứng minh rằng
a. f (x) 8x9 9x8 1g(x) (x 1)2 
b. f (x) x99 x98 ... x 1; g(x) x4 x3 x2 x 1
c. f (x) x8n x4n 1; g(x) x2n xn 1 
d. f (x) x100 x20 1; g(x) x40 x20 1
e. f (x) x10 10x 9; g(x) (x 1)2
 Lời giải
a. Ta có f (x) 8x9 9x8 1 8x9 8 9x8 9 8(x9 1) 9(x8 1) 8(x 1)(x8 x7 ... 1)
 9(x 1)(x7 x6 x5 ... 1) (x 1)(8x8 x7 ..... x 1)
Cách 1: Ta có 8x8 x7 ..... x 1 có tổng các hệ số = 0 (x 1) f (x)(x 1)2 
Cách 2: (x 1)(8x8 x7 ..... x 1) (x 1)(8x8 8x7 7x7 7x6 ..... x 1)
 (x 1)2 (8x7 7x6 ... 2x 1)(x 1)2
b. f (x) x99 x98 ... x 1 (x99 ... x95 ) ...(x4 x3 ... x 1)
 (x4 ... 1)(x95 x90 ... x5 1)g(x)
Cách 2: Ta có (x 1). f (x) x100 1 [(x5 )20 1](x5 1) (x 1).g(x) f (x)g(x)
c. Ta có 
 f (x) x8n x4n 1 (x4n )2 2.x4n 1 x4n (x4n 1)2 (x2n )2 (x4n x2n 1)(x4n x2n 1)
Lại có: x4n x2n 1 (x2n xn 1)(x2n xn 1) f (x)g(x)
d. Đặt t x20 f (t) t5 t 1; g(t) t 2 t 1
Ta có: f (t) t5 t 2 t 2 t 1 t 2 (t3 1) (t 2 t 1) (t 2 t 1)(t3 t 2 1) f (x)g(x)
e. f (x) (x10 1) (10x 10) (x 1)(x9 x8 ... x 1 10) (x 1)[ x9 1 ... (x 1)]
= x 1 2 (x8 2x7 ... 8x 9) f (x)g(x)
 3 f (x) x99 x88 .. x11 1 (x99 x9 ) (x88 8) ...(x11 x) x9 x8 ... x 1
 x9 (x90 1) x8 (x80 1) ... x(x10 1) g(x) x9[(x10 )9 1] x8[(x10 )8 1] ... x(x10 1) g(x)
   
 x10 1 x10 1 x10 1
 f (x)g(x)
d. Ta có f (x) x3m 1 x3m 2 1 (x3m 1 x) (x3m 2 x2 ) (x2 x 1)
x3m 1 x x(x3m 1) x[(x3 )m 1]x3 1 (x 1)(x2 x 1)
x3m 2 x2 x2 (x3m 1) x2[(x3 )m 1]x3 1 (x 1)(x2 x 1)
 f (x)g(x)
e. f (x) x6m 4 x6n 2 1 x6m 4 x4 x6n 2 x2 x4 x2 1
 x4 [(x6 )m 1] x2 [(x6 )n 1] (x4 x2 1)
  
 x6 1 x6 1
x6 1 (x3 )2 1 (x3 1)(x3 1); x4 x2 1 (x2 x 1)(x2 x 1) f (x)g(x)
  
 x2 x 1 x2 x 1
Cách 3: Sử dụng các phép biến đổi tương đương
Muốn chứng minh f (x) chia hết cho g(x) ta đi chứng minh 
 f (x) g(x)g(x)
 f (x)g(x)
 f (x) g(x)g(x)
 Bài 4: 
Chứng minh rằng f (x) x99 x88 ... x11 1g(x) x9 x8 ... x 1
 Lời giải:
 f (x) g(x) x99 (x90 1) x8 (x80 1) ... x(x10 1)
Ta có:   
 x10 1 x10 1 x10 1
Mà x10 1 (x 1)(x9 x8 x7 ... x 1) f (x) g(x)g(x)
Lại có: g(x)g(x) f (x)g(x)
Cách 4: Chứng tỏ rằng mọi nghiệm của đa thức chia đều là nghiệm của đa thức bị chia
- Cách này áp dụng với những bài toán mà đa thức chia dễ tìm được nghiệm
 Bài 5: Chứng minh rằng
a. [f (x) (x2 x 1)10 (x2 x 1)10 2]g(x) x2 x
b. f (x) (x 1)2n x2n 2x 1; g(x) x(x 1)(2x 1)n N
 5 Bài 7: HSG Gia Lâm, năm học 2020 - 2021
 2020 2020
Chứng minh rằng đa thức A x x2 x 1 x2 x 1 2 chia hết cho đa thức 
 B x x 1
 Lời giải
 2020 2020
Chứng minh rằng đa thức A x x2 x 1 x2 x 1 2 chia hết cho đa thức 
 B x x 1
Ta thấy đa thức B x x 1 có nghiệm là x 1
 2020 2019
Mà A 1 12 1 1 12 1 1 2 0 nên đa thức A x phải có 1 nhân tử là x 1. Vậy nên 
đa thức A x chia hết cho đa thức B x 
 7 Bài 3: Tìm dư trong phép chia
a. f (x) x100 x99 ... x 1; g(x) (x 1)(x2 1) 
b. f (x) x10 x9 ... x 1; g(x) x2 x 1
 Lời giải
a) Ta có g x có 101 số hạng, nhóm 4 số hạng, dư là 1 
b) Ta có: f (x) x10 x9 ... x 1 (x10 x) (x9 1) (x8 x2 ) (x7 x) (x6 1) (x5 x2 ) (x4 x)
 3
 (x 1) x 1
 du
Vậy đa thức dư là x 1
 Bài 4: Tìm dư trong phép chia
 2
 f x x 2 x 4 x 6 x 8 2008; g x x 10x 21 
 Lời giải
 2 2
Ta có f x x 2 x 4 x 6 x 8 2008 x 10x 16 x 10x 24 2008 
Đặt t x2 10x 21(t 3;t 7) P(t) t 2 2t 1993
 du
 Bài 5: HSG Yên Dũng, năm học 2019 - 2020
Tìm số dư trong phép chia x 3 x 5 x 7 x 9 2035 cho x2 12x 30
 Lời giải
Ta có x 3 x 5 x 7 x 9 2035
 x2 12x 27 x2 12x 35 2035
Đặt x2 12x 30 t , ta có x 3 x 5 x 7 x 9 2035
 t 3 t 5 2035 t 2 2t 15 2035 t(t 2) 2020
Do đó x 3 x 5 x 7 x 9 2035= x2 12x 30 x2 12x 32 2020
Vậy số dư trong phép chia x 3 x 5 x 7 x 9 2035 cho x2 12x 30 là 2020
 Bài 6: HSG Quế Võ, năm học 2020 - 2021
Cho đa thức P(x) x 5 x 10 x 15 x 20 2016. Tìm số dư trong phép chia P x cho đa 
thức x2 25x 120
 9 2. Cách 2: Xét giá trị riêng (phép chia ảo)
 Bài 1: Tìm số dư của f x cho g x , biết rằng
a. f (x) x7 x5 x3 1; g(x) x2 1 
b. f (x) x10 x 8 ...x 1; g(x) x2 x 2
c. f (x) (x 1)(x 3)(x 5)(x 7) 1999; g(x) x2 8x 12
 Lời giải
a) Gọi thương phép chia là q x và dư là ax b , ta có x7 x5 x3 1 (x2 1).q(x) ax b, x 
Vì đẳng thức đúng với mọi x nên ta chọn x 1 và x 1, được:
 x 1 4 a b a 3
 du :3x 1
 x 1 2 a b b 1
b. Ta có g(x) x2 x 2 (x 1)(x 2)
Thực hiện phép chia f x cho g x ta được: f (x) (x 1)(x 2).q(x) ax+b
 x 1 1 a b a 682
Cho du : 682x 683
 x 2 2047 2a b b 683
c. Cách 1: 
 f (x) (x 1)(x 7)(x 3)(x 5) 1999 x4 16x3 86x2 176x 2014 (x 2)(x 6).q(x) ax+b
 x 2 1984 b 2a a 0
Cho du :1984
 x 6 1984 b 6a b 1984
 2 2
Cách 2: Đặt t x 8x 7 f (t) t(t 8) 1999 (t 8t 15) 1984 (t 3)(t 5) 1 984
 du
 Bài 2: Tìm đa thức f x biết rằng:
a. f x chia cho x 3 thì dư 7, chia cho x 2 thì dư 5, chia cho x 2 x 3 thì được thương 
là 3x và còn dư.
b. f x chia cho x 2 thì dư 5, chia cho x 3 thì dư 7, chia cho x 2 x 3 thì được thương 
là x2 1 và còn dư.
c. f x chia cho x 3 thì dư -5, chia cho x 2 thì dư 5, chia cho x2 x 6 thì được thương là 
 x2 2 và còn dư.
 Lời giải:
 11 2 2 b 2(2)
+) f (x) (x 2)(x 1) a(x 1) bx c a (a,b,c) (1,2,4)
 du c a 3(3)
 du : x2 2x 4
 Bài 5: HSG Hà Trung Thanh Hóa, năm học 2020 - 2021
Xác định đa thức f (x) biết f (x) chia cho x 1 dư 4 và chia cho x2 x 2 được thương là 5x2
 Lời giải
Gọi A x , B x là các đa thức sao cho
 f (x) x 1 A x 4
 f (x) x 2 B x 1
 x 2 f x x 2 x 1 .A x 4 x 2 
Khi đó, 
 x 1 f x x 1 (x 2)B x 1 x 1 
 x 2 f x x 2 (x 1) A x B x 3x 9
 A x B x 
 3 f x x 2 x 1 A x B x 3x 9 f x x 1 x 2 x 3 * 
 3
Theo bài ra khi chia f x cho x2 x 2 x 1 x 2 ta được thương là 5x2 nên 
 A x B x 
 5x
 3
Khi đó * trở thành: f x x 1 x 2 .5x2 x 3
Vậy f x 5x2 x 1 x 2 x 3
 Bài 6: HSG Cẩm Thủy, năm học 2020 - 2021
Đa thức f x khi chia cho x 1 dư 4, khi chia cho x2 1 dư 2x 3. Tìm phần dư khi chia f x 
cho x 1 x2 1 .
 Lời giải
Giả sử f x x 1 x2 1 .g x + ax2 bx c
+ Vì f x chia cho x 1 dư 4 nên f 1 4 a b c 4 (1)
 2 2 2
Mà f x x 1 x 1 .g x + a x 1 bx c a x 1 x 1 .g x a bx c a
 13