Chuyên đề Bồi dưỡng học sinh giỏi Toán 8 - Chủ đề 8: Các bài toán về định lí Ta-lét

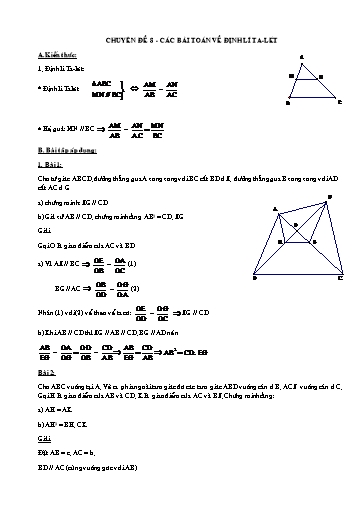
 CHUYEÂN ÑEÀ 8 - CAÙC BAØI TOAÙN VEÀ ÑÒNH LÍ TA-LEÙT
A.Kieán thöùc: A
1. Ñònh lí Ta-leùt:
 M N
 ABC  AM AN
* Ñònh lí Taleùt  = 
 MN // BC AB AC
 B C
 AM AN MN
* Heä quaû: MN // BC = 
 AB AC BC
B. Baøi taäp aùp duïng:
1. Baøi 1:
Cho töù giaùc ABCD, ñöôøng thaúng qua A song song vôùi BC caét BD ôû E, ñöôøng thaúng qua B song song vôùi AD 
caét AC ôû G
 B
a) chöùng minh: EG // CD
 A
b) Giaû söû AB // CD, chöùng minh raèng AB2 = CD. EG
 O
Giaûi
 E G
Goïi O laø giao ñieåm cuûa AC vaø BD
 OE OA
a) Vì AE // BC = (1)
 OB OC
 D C
 OB OG
 BG // AC = (2)
 OD OA
 OE OG
Nhaân (1) vôùi (2) veá theo veá ta coù: = EG // CD
 OD OC
b) Khi AB // CD thì EG // AB // CD, BG // AD neân
 AB OA OD CD AB CD
 = = AB2 CD. EG
 EG OG OB AB EG AB
Baøi 2: 
Cho ABC vuoâng taïi A, Veõ ra phía ngoaøi tam giaùc ñoù caùc tam giaùc ABD vuoâng caân ôû B, ACF vuoâng caân ôû C. 
Goïi H laø giao ñieåm cuûa AB vaø CD, K laø giao ñieåm cuûa AC vaø BF. Chöùng minh raèng:
a) AH = AK
b) AH2 = BH. CK
Giaûi 
Ñaët AB = c, AC = b. 
BD // AC (cuøng vuoâng goùc vôùi AB) Cho töù giaùc ABCD, caùc ñieåm E, F, G, H theo thöù töï chia trong caùc caïnh AB, BC, 
 B
CD, DA theo tæ soá 1:2. Chöùng minh raèng: E
 A
a) EG = FH
 P
b) EG vuoâng goùc vôùi FH H F
 O
Giaûi D Q
Goïi M, N theo thöù töï laø trung ñieåm cuûa CF, DG N M
 1 1 BM 1 BE BM 1
Ta coù CM = CF = BC = = = G
 2 3 BC 3 BA BC 3
 C
 EM BM 2 2
 EM // AC = EM = AC (1)
 AC BE 3 3
 NF CF 2 2
T­¬ng tù, ta cã: NF // BD = NF = BD (2)
 BD CB 3 3
mµ AC = BD (3)
Tõ (1), (2), (3) suy ra : EM = NF (a)
 1
T­¬ng tù nh­ trªn ta cã: MG // BD, NH // AC vµ MG = NH = AC (b)
 3
MÆt kh¸c EM // AC; MG // BD Vµ AC  BD EM  MG E· MG = 900 (4)
T­¬ng tù, ta cã: F· NH = 900 (5)
Tõ (4) vµ (5) suy ra E· MG = F· NH = 900 (c)
Tõ (a), (b), (c) suy ra EMG = FNH (c.g.c) EG = FH
b) Gäi giao ®iÓm cña EG vµ FH lµ O; cña EM vµ FH lµ P; cña EM vµ FN lµ Q th× 
P· QF = 900 Q· PF + Q· FP = 900 mµ Q· PF = O· PE (®èi ®Ønh), O· EP = Q· FP ( EMG = FNH)
Suy ra E· OP = P· QF = 900 EO  OP EG  FH
5. Bµi 5: 
Cho h×nh thang ABCD cã ®¸y nhá CD. Tõ D vÏ ®­êng th¼ng song song víi BC, c¾t AC t¹i M vµ AB t¹i K, Tõ C 
vÏ ®­êng th¼ng song song víi AD, c¾t AB t¹i F, qua F ta l¹i vÏ ®­êng th¼ng song song víi AC, c¾t BC t¹i P. 
Chøng minh r»ng
a) MP // AB
 D C
b) Ba ®­êng th¼ng MP, CF, DB ®ång quy
Gi¶i
 CP AF P
a) EP // AC = (1) M I
 PB FB
 CM DC
 AK // CD = (2)
 AM AK A K F B Cho tø gi¸c ABCD, AC vµ BD c¾t nhau t¹i O. §­êng th¼ng qua O vµ song song víi BC c¾t AB ë E; ®­êng th¼ng 
song song víi CD qua O c¾t AD t¹i F
a) Chøng minh FE // BD
b) Tõ O kÎ c¸c ®­êng th¼ng song song víi AB, AD c¾t BD, CD t¹i G vµ H. 
Chøng minh: CG. DH = BG. CH
Bµi 2: 
Cho h×nh b×nh hµnh ABCD, ®iÓm M thuéc c¹nh BC, ®iÓm N thuéc tia ®èi cña tia BC sao cho BN = CM; c¸c ®­êng 
th¼ng DN, DM c¾t AB theo thø tù t¹i E, F. 
Chøng minh: 
a) AE2 = EB. FE
 2
 AN 
b) EB = . EF
 DF