Chuyên đề Biểu diễn hình học của số phức - Đại số 12

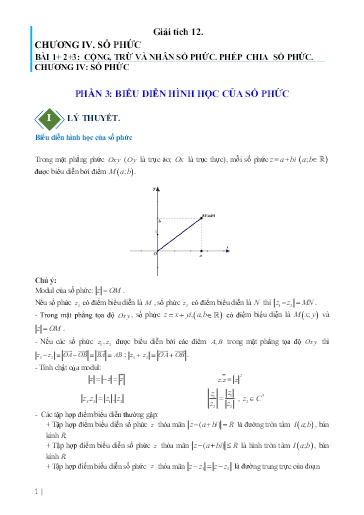
 Giải tích 12. 
CHƯƠNG IV. SỐ PHỨC 
BÀI 1+ 2+3: CỘNG, TRỪ VÀ NHÂN SỐ PHỨC. PHÉP CHIA SỐ PHỨC. 
CHƯƠNG IV: SỐ PHỨC 
 PHẦN 3: BIỂU DIỄN HÌNH HỌC CỦA SỐ PHỨC 
 I LÝ THUYẾT. 
 = 
Biểu diễn hình học của số phức 
Trong mặt phẳng phức Oxy (Oy là trục ảo; Ox là trục thực), mỗi số phức z a bi a; b 
được biểu diễn bởi điểm M a; b . 
Chú ý: 
Modul của số phức: z OM . 
Nếu số phức z1 có điểm biểu diễn là M , số phức z2 có điểm biểu diễn là N thì z12 z MN . 
- Trong mặt phẳng tọa độ Oxy , số phức z x yi,, a b có điểm biểu diễn là M x; y và 
 z OM . 
- Nếu các số phức zz12, được biểu diễn bởi các điểm AB, trong mặt phẳng tọa độ Oxy thì 
 z12 z OA OB BA AB ; z12 z OA OB . 
- Tính chất của modul: 
 2
 z z z z. z z 
 z1 z1 *
 z1.. z 2 z 1 z 2 , zC2 
 zz22
- Các tập hợp điểm biểu diễn thường gặp: 
 + Tập hợp điểm biểu diễn số phức z thỏa mãn z () a bi R là đường tròn tâm I a; b , bán 
 kính R. 
 + Tập hợp điểm biểu diễn số phức thỏa mãn z () a bi R là hình tròn tâm , bán 
 kính R. 
 + Tập hợp điểm biểu diễn số phức thỏa mãn z z12 z z là đường trung trực của đoạn 
1 | 
 71
 suy ra M ; là điểm biểu diễn của số phức z . 
 22
 Ví DỤ 4 
 i2017
 [2D4-1.2-1] Trong mặt phẳng phức, tìm điểm M biểu diễn số phức z . 
 34 i
 Lời giải 
 2 1008 1008
 i2017 ii. i. 1 i 3 4 i 43
 Ta có zi . 
 34 i 34 i 34 i 25 2525
 43
 Suy ra M ; là điểm biểu diễn cho số phức z.. 
 25 25
 Ví DỤ 5 
 17 i
 [2D4-1.2-2] Cho số phức z thỏa mãn iz 12 i . Xác định điểm A biểu diễn số phức z . 
 13 i
 Lời giải 
 Ta có: 
 1 7ii 3
 iz 12 i iz 12(2) i i iz 3 i z 13 i z 13 i . 
 13 ii
 Suy ra A 1;3 là điểm biểu diễn của số phức z . 
 Ví DỤ 6 
[2D4-1.2-3] Tìm tọa độ điểm biểu diễn số phức z thỏa mãn z 3 z 5 i z 4 . 
 Lời giải 
 Giả sử z x yi,, x y z x yi . 
 Khi đó 
 zz 3 5 iz 4 xyi 3 xyi 5 ixyi 4 4 xyi 2 5 yx 4 i 
 6
 x 
 4x 5 y 4 x y 5 7
 . 
 2y x 4 x 2 y 4 11
 y 
 7
 6 11
 số phức cần tìm là zi . 
 77
 6 11
 Vậy điểm biểu diễn cho số phức z là M ; . 
 77
 Ví DỤ 7 
 5
[2D4-1.2-3] Cho số phức z thỏa mãn điều kiện z 2 3 i z 1 9 i . Số phức w có điểm biểu 
 iz
diễn là điểm nào trong các điểm ABCD, , , ở hình bên dưới? 
3 | 
 Với z a bi a, b ta có z 2 16 i z 1 i 0 trở thành 
 a 2 b 16 i z i z 
 22
 az 2 a 21 a b 
 bz 16 22
 16 b a b 2 
 Lấy 1 trừ 2 theo vế ta được a b 14 0 b 14 a . Thay vào 1 ta được 
 2 0 az 2 20 do 20 
 a 2 a2 14 a a 8 suy ra b 6. 
 2
 aa 32 192 0
 Do đó zi 86 có z 10 20 (thỏa mãn điều kiện z 20 ). 
 Vậy điểm biểu diễn cho số phức z là M 8;6 . 
 Ví DỤ 10 
[2D4-1.2-3] Cho số phức z a bi a, b , a 0 thỏa mãn z. z 6 z 3 z z 91 72 i . Tìm 
tọa độ điểm biểu diễn số phức z . 
 Lời giải 
 Với z a bi a, b , a 0 ta có z.z 6 z 3 z z 91 72 i trở thành: 
 2 2 2 2
 2 2 2 2 a b 6 a b 91
 a b 6 a b 6 bi 91 72 i 
 6b 72
 aa2 144 13 5
 aa22 144 6 144 91 0 
 a2 144 7 a 5 . 
 b 12 
 b 12
 b 12 
 a 5
 Do a 0 nên ta được . 
 b 12
 Vậy điểm biểu diễn cho số phức z là M 5;12 . 
 Ví DỤ 11 
Trong mặt phẳng phức, cho tam giác ABC với ABC,, lần lượt là ba điểm biểu diễn của ba số 
phức zi1 1 , zi2 2 , zi3 42. Tìm tập hợp các điểm M x; y trên mặt phẳng phức sao cho 
 AM là đường trung tuyến ABC . 
 Lời giải 
 Gọi M x; y là điểm biểu diễn số phức z x yi trên mặt phẳng phức. 
 Gọi I là trung điểm BC . 
 zz 
 Khi đó I là điểm biểu diễn của số phức z 232 I 2;0 . 
 4 2
 Ta có: z41 z 1 i AI 1; 1 . 
 Phương trình đường trung tuyến AI qua A 1;1 và nhận AI 1; 1 là véc-tơ chỉ 
 phương là: 
5 | 
 4i
[2D4-1.2-2] Xét các điểm ABC,, trong mặt phẳng phức theo thứ tự biểu diễn các số , 
 i 1
 26 i
 1 ii 1 2 , . Chứng minh ABC là tam giác vuông cân. 
 3 i
 Lời giải 
 4i 41ii 
 Ta có: 2 2iA 2; 2 
 ii 112
 1 i 1 2 i 3 i B 3;1 
 26 i 2 6ii 3 
 2iC 0;2 . 
 33 ii22
 BA BC
 Dễ thấy: nên ABC là tam giác vuông cân tại B . 
 BA.0 BC 
 Ví DỤ 14 
[2D4-1.2-2] Trên mặt phẳng tọa độ, các điểm A , B , C theo thứ tự biểu diễn các số phức 23 i , 
 3 i , 12 i . Trọng tâm G của tam giác ABC biểu diễn số phức z . Tìm z . 
 Lời giải 
 Ta có: A 2;3 , B 3;1 , C 1;2 . 
 2 3 1
 x 2
 G 3
 Vì G là trọng tâm tam giác ABC nên 
 3 1 2
 y 2
 G 3
 G 2;2 z 2 2 i . 
 Ví DỤ 15 
[2D4-1.2-2L] Cho ba số phức zi1 23, zi2 4 , zi3 2 . Gọi A , B , C lần lượt là các điểm 
biểu diễn số phức z1 , z2 , z3 trong mặt phẳng phức. Số phức z4 x yi biểu thị điểm D sao cho tứ 
giác ABCD là hình bình hành. Tìm tọa độ điểm D . 
 Lời giải 
 Ta có: 
 zi1 23 A 2; 3 
 zi2 4 B 0;4 
 zi3 2 C 2;1 
 Và D x; y suy ra AB 2;7 , DC 2 x ;1 y 
 22 x x 4
 ABCD là hình bình hành AB DC D 4; 6 . 
 17 y y 6
 Vậy D 4; 6 . 
 Ví DỤ 16 
[2D4-1.2-3] Cho hai điểm A , B là hai điểm biểu diễn hình học số phức theo thứ tự z0 , z1 khác 0 
 22
và thỏa mãn đẳng thức z0 z 1 z 0 z 1.Chứng minh tam giác OAB đều. 
7 | 
 Lời giải 
 Gọi M x, y là điểm biểu diễn của số phức z . 
 22 x 0
 1 x yi x yi 2 xy 2 xy 
 y 0
 Vậy điểm biểu diễn số phức z trên mặt phẳng phức là tất cả các điểm M x, y nằm trên 
 hai trục tọa độ. 
 Ví DỤ 3 
Tìm các điểm biểu diễn số phức z trên mặt phẳng phức sao cho z 2 là số thuần ảo. 
 Lời giải 
 Gọi là điểm biểu diễn số phức trên mặt phẳng phức. 
 Ta có: z2 x yi 2 x 2 y 2 2 xyi 
 22 yx 
 Theo đề: là số thuần ảo xy 0 
 yx 
 Vậy tập hợp các điểm biểu diễn số phức thỏa đề là 2 đường phân giác của 
 các góc phần tư trong mặt phẳng phức: yx và yx . 
 Ví DỤ 4 
 zi 
 Tìm các điểm biểu diễn số phức trên mặt phẳng phức sao cho là số thực. 
 zi 
 Lời giải 
 Gọi là điểm biểu diễn số phức trên mặt phẳng phức. 
 2 2
 zi x x y i x x y i x 1 y i x 12 y xyi
 Ta có: . 
 z i x 1 y i x22 11 y 22 x y 
 x 0
 zi 20xy 
 Theo đề: y 0 . 
 2 2 
 zi xy 10 
 xy; 0;1 
 M x; y z x yi
 Vậy tập hợp các điểm trên mặt phẳng phức biểu diễn số phức thỏa đề là 2 
 trục tọa độ x 0 , y 0 và khác điểm 0;1 . 
 Ví DỤ 5 
[2D4-3.2-1] Trong mặt phẳng toạ độ Oxy , cho số phức z thỏa mãn: zz 1 . Gọi d là đường 
 thẳng biểu diễn số phức z .Tính khoảng cách từ O đến d . 
 Lời giải 
9 |