Chuyên đề Bài tập bảng biến thiên và các dạng toán liên quan - Đại số 12

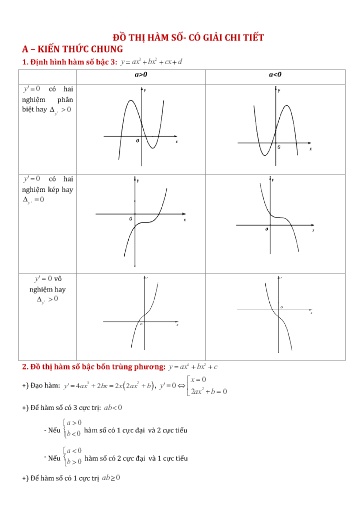
 ĐỒ THỊ HÀM SỐ- CÓ GIẢI CHI TIẾT 
A – KIẾN THỨC CHUNG 
1. Định hình hàm số bậc 3: y ax32 bx cx d 
 a>0 a<0 
y'0 có hai 
nghiệm phân 
biệt hay 0 
 y/
y'0 có hai 
nghiệm kép hay 
 0 
 y/
 y'0 vô 
 nghiệm hay 
 0 
 y/
2. Đồ thị hàm số bậc bốn trùng phương: y ax42 bx c 
 x 0
 32y'0 
+) Đạo hàm: y' 4 ax 2 bx 2 x 2 ax b , 2 
 20ax b
+) Để hàm số có 3 cực trị: ab 0 
 a 0
 - Nếu hàm số có 1 cực đại và 2 cực tiểu 
 b 0
 a 0
 - Nếu hàm số có 2 cực đại và 1 cực tiểu 
 b 0
+) Để hàm số có 1 cực trị ab 0 
4. Đồ thị hàm số chứa dấu giá trị tuyệt đối 
Dạng 1: Từ đồ thị (C) của hàm số y f x , suy ra cách vẽ đồ thị (G) của hàm số y f x 
 f x khi f x 0
 y f x 
 f x khi f x 0 
Suy ra GCC  12 
+ C là phần đồ thị (C) nằm phía trên trục hoành y 0 . 
 1 C 
+ C là phần đối xứng qua trục hoành của phần đồ thị (C) nằm phía dưới trục hoành y 0 
 2 C 
Dạng 2: Từ đồ thị (C) của hàm số , suy ra cách vẽ đồ thị (H) của hàm số y f x 
Vì xx nên là hàm số chẵn, suy ra đồ thị (H) nhận trục tung làm trục đối xứng. Vì Suy 
ra ()HCC  34 
+ C3 là phần đồ thị của (C) nằm bên phải trục tung x 0 . 
+ C4 là phần đối xứng của qua trục tung. 
B – BÀI TẬP 
DẠNG 1: BẢNG BIẾN THIÊN VÀ CÁC BÀI TOÁN LIÊN QUAN 
Câu 1. Bảng biến thiên sau là bảng biến thiên của hàm số nào sau đây? 
 2 
 0 0 
 A. y x32 31 x . B. y x32 3 x 2. C. y x32 31 x . D. y x3 32 x . 
Câu 2. Bảng biến thiên sau đây là của hàm số nào ? Câu 6. Bảng biến thiên sau đây là của hàm số nào ? 
 x -∞ 1 +∞
 y' + 0 +
 +∞
 y 1
 -∞
 x3 2
 A. y x42 31 x B. yx 3 1. C. y x42 31 x . D. y x2 x 
 33
Câu 7.Bảng biến thiên sau là của hàm số nào? 
 x 
 y – – 
 2 
 y 
 2 
 21x 21x 2x 23x 
 A. y . B. y . C. y . D. y . 
 x 1 x 1 x 1 x 1
Câu 8. Hàm số nào sau đây có bảng biến thiên như hình bên 
 x 2 
 y 
 2 
 y 
 2 
 21x 23x x 3 27x 
 A. y . B. y . C. y . D. y . 
 x 2 x 2 x 2 x 2
Câu 9. Bảng biến thiên sau đây là của hàm số nào? 
 x 1 
 y + + 
 y . . 
 2 
 23x 23x 21x 22x 
 A. y . B. y . C. y . D. y . 
 x 1 x 1 1 x 1 x
Câu 10. Bảng biến thiên ở hình dưới là của một trong bốn hàm số được liệt kê dưới đây. Hãy tìm hàm 
số đó. D. Hàm số đồng biến trên các khoảng 1;0 và 1; . 
Câu 14. Cho hàm số có bảng biến thiên ở hình bên. Khẳng định 
nào sau đây là khẳng định sai ? x -∞ 0 2 +∞
 y' -- 0 + 0 --
A. Hàm số có 2 cực trị. 
 +∞ 3
B. Hàm số có giá trị cực đại bằng 3 . y
 -1
 -∞
C. Hàm số có giá trị lớn nhất bằng , giá trị nhỏ nhất bằng 1. 
D. Hàm số đạt cực tiểu tại x 0 . 
Câu 15. Cho hàm số y f x xác định, liên tục trên và có bảng biến thiên: 
 –∞ +∞ 
 0 
 . 
Mệnh đề nào dưới đây đúng ? 
 A. Hàm số đồng biến trên khoảng ;1 . B. Đồ thị hàm số không có tiệm cận ngang. 
 C. Hàm số đạt cực trị tại x 2. D. Hàm số có giá trị lớn nhất bằng 1. 
Câu 17. Cho hàm số y f() x xác định và liên tục trên và có bảng biến thiên 
Khẳng định sai? 
 A. Hàm số có giá trị lớn nhất bằng 4 . 
 B. Hàm số đồng biến trên khoảng (0;2) . 
 C. Hàm số đạt cực tiểu tại điểm x 0 .. 
 D. Hàm số đạt cực đại tại điểm x 2 . 
Câu 19. Cho hàm số y f x xác định, liên tục trên 
 ;1 , 1; và có bảng biến thiên :. 1. Phương trình f x m có nghiệm khi và chỉ khi 
m 2 . 
2. Cực đại của hàm số là -3. 
3. Cực tiểu của hàm số là 2. 
4. Đường thẳng x 2 là tiệm cận đứng của đồ thị. 
5. Đồ thị hàm số có đường tiệm cận ngang. 
Số mệnh đề đúng là: 
 A. 2 . B. 1. C. 4 . D. 3 . 
Câu 24. Cho hàm số y f x có bảng biến thiên như hình bên. Khi đó tất cả các giá trị của m để 
phương trình f x m 1 có ba nghiệm thực là 
 A. m 3;5 . B. m 4;6 . C. m ;3  5; . D. m 4;6 . 
 PHẦN HƯỚNG DẪN GIẢI 
 DẠNG 1: BẢNG BIẾN THIÊN VÀ CÁC BÀI TOÁN LIÊN QUAN 
Câu 1. Bảng biến thiên sau là bảng biến thiên của hàm số nào sau đây? 
 2 
 0 0 
 A. . B. C. . D. . 
Hướng dẫn giải: 
 Chọn đáp án B. 
 Ta có lim y nên loại đáp án A. 
 x 
 32 32 32 3
 Vì yy 02 x 31 x nên loại đáp án yC . x 3 x 2. y x 31 x y x 32 x –∞ 0 +∞ 
 – 0 + 0 – 0 + 
 +∞ +∞ 
 A. y x422 x 1.. B. y x422 x 1.. 
 C. y x42 x 1. . D. y x422 x 1.. 
Hướng dẫn giải: 
 Chọn đáp án B. 
 y x422 x 1.
 x 1
 3 
 y' 4 x 4 x ; y ' 0 x 1
 x 0
 Cực trị của hàm số: 
 * Hàm số đạt cực tiểu tại hai điểm x 1vàx 1;yyCT 1 2. 
 * Hàm số đạt cực đại tại điểm x0; yCD y 0 1. 
 2 x 2
 y 0 6 x 6 x 12 0 . 
 x 1
Câu 5. Bảng biến thiên trong h nh v dưới đây là bảng biến thiên của hàm số nào? 
 x 1 0 1 
 y - 0 + 0 - 0 + 
 -3 
 y 
 4 4 
 A. y x42 23 x . B. y x42 23 x . C. y x42 x 3. D. y x42 23 x . 
Hướng dẫn giải: 
 Chọn đáp án B. 
 Thay x 1 vào hàm số y x42 23 x ta có y 1 1 42 2 1 3 4. Vậy hàm số này 
 thỏa mãn bảng biến thiên bên trên. 
Câu 6. Bảng biến thiên sau đây là của hàm số nào ?