Chuyên đề 8 - Chương VIII, Bài 3: Nhị thức Newton - Toán 10 Chân trời sáng tạo

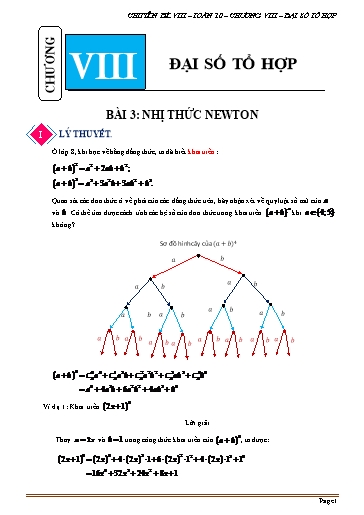
 CHUYÊN ĐỀ VIII – TOÁN 10 – CHƯƠNG VIII – ĐẠI SỐ TỔ HỢP
 VIII ĐẠI SỐ TỔ HỢP
 CHƯƠNG
 BÀI 3: NHỊ THỨC NEWTON
I LÝ THUYẾT.
= Ở lớp 8, khi học về hằng đẳng thức, ta đã biết khai triển:
=
 2 2 2
= a b a 2ab b ;
I a b 3 a3 3a2b 3ab2 b3.
 Quan sát các đơn thức ở vế phải của các đẳng thức trên, hãy nhận xét về quy luật số mũ của a 
 n
 và b . Có thể tìm được cách tính các hệ số của đơn thức trong khai triển a b khi n 4;5 
 không?
 Sơ đồ hình cây của ( + )4
 4 0 4 1 3 2 2 2 3 3 4 4
 a b C4 a C4a b C4 a b C4 ab C4 b
 a4 4a3b 6a2b2 4ab3 b4
 4
 Ví dụ 1: Khai triển 2x 1 .
 Lời giải
 4
 Thay a 2x và b 1 trong công thức khai triển của a b , ta được:
 2x 1 4 2x 4 4 2x 3 1 6 2x 2 12 4 2x 13 14
 16x4 32x3 24x2 8x 1
 Page 1 CHUYÊN ĐỀ VIII – TOÁN 10 – CHƯƠNG VIII – ĐẠI SỐ TỔ HỢP
 BÀI TẬP.
Câu 1. Khai triển các đa thức:
 a) x 3 4 ; b) 3x 2y 4 ;
 c) x 5 4 x 5 4 ; d) x 2y 5
 Lời giải
 4 0 4 1 3 2 2 2 1 3 0 4
 a) x 3 C4 x C4 x 3 C4 x 3 C4 x 3 C4 3 
 x4 12x3 54x2 108x 81 
 4 0 4 1 3 1 2 2 2 1 3 0 4
 b) 3x 2y C4 3x C4 3x 2y C4 3x 2y C4 3x 2y C4 2y 
 81x4 216x3 y 216x2 y2 96xy3 16y4
 4 4 0 4 1 3 2 2 2 3 3 4 4 0 4
 c) x 5 x 5 C4 x C4 x 5 C4 x 5 C4 x5 C4 5 C4 x
 1 3 2 2 2 3 3 4 4
 C4 x 5 C4 x 5 C4 x5 C4 5
 0 4 2 2 2 4 4 4 2 4 2
 2 C4 x C4 x 5 C4 5 2. x 150x 625 2x 300x 1250
 5 0 5 1 4 2 3 2 3 2 3 4 4 5 5
 d) x 2y C5 x C5 x ( 2y) C5 x 2y C5 x 2y C5 x 2y C5 2y 
 x5 10x4 y 40x3 y2 80x2 y3 80xy4 32y5
Câu 2. Tìm hệ số của x4 trong khai triển của 3x 1 5
 Lời giải
 3 2 3 2 4
 Số hạng thứ 4 của khai triển là C5 3x 1 90x . Vậy hệ số của x trong khai triển là 
 90 .
 5 5
Câu 3. Biểu diễn 3 2 3 2 dưới dạng a b 2 với a,b là các số nguyên.
 Lời giải
 Nhận xét: 
 5 5 0 5 1 4 2 3 2 3 2 3 4 4 5 5
 a b a b C5 a C5a b C5 a b C5 a b C5 ab C5 b
 0 5 1 4 2 3 2 3 2 3 4 4 5 5
 C5 a C5a b C5 a b C5 a b C5 ab C5 b 
 1 4 3 2 3 5 5
 2 C5a b C5 a b C5 b 
 3 5
 Do đó a b 5 a b 5 2 C134 2 C3 32 2 C5 2 
 5 5 5 
 2 405 2 180 2 4 2 1178 2
 Page 3 CHUYÊN ĐỀ VIII – TOÁN 10 – CHƯƠNG VIII – ĐẠI SỐ TỔ HỢP
TỔNG QUÁT VỀ CÔNG THỨC NHỊ THỨC NIU-TƠN
1. CÔNG THỨC NHỊ THỨC NEWTON
 n
 Khai triển a b được cho bởi công thức sau:
 Với a,b là các số thực và n là sô nguyên dương, ta có
 n
 n k n k k 0 n 1 n 1 k n k k n n
 a b Cn a b Cn a Cna b ... Cn a b ... Cn b . 1 
 k 0
 Quy ước a0 b0 1 
 Công thức trên được gọi là công thức nhị thức Newton (viết tắt là Nhị thức Newton).
 Trong biểu thức ở VP của công thức (1)
 a) Số các hạng tử là n 1.
 b) Số các hạng tử có số mũ của a giảm dần từ n đến 0, số mũ của b tăng dần từ 0 đến n, nhưng 
 tổng các số mũ của a và b trong mỗi hạng tử luôn bằng n.
 c) Các hệ số của mỗi hạng tử cách đều hai hạng tử đầu và cuối thì bằng nhau.
 k n k k
 d) Số hạng thứ k (số hạng tổng quát) của khai triển là: Tk 1 Cn a b .
2.HỆ QUẢ
 n 0 1 n
 Với a b 1, thì ta có 2 Cn Cn ... Cn .
 0 1 k k n n
 Với a 1; b 1, ta có 0 Cn Cn ... 1 Cn ... 1 Cn 
3. CÁC DẠNG KHAI TRIỂN CƠ BẢN NHỊ THỨC NEWTON
 n 0 n 1 n 1 2 n 2 k n k n 1 n
 ✓ x 1 Cn x Cn x Cn x ... Cn x ... Cn x Cn
 n 0 1 2 2 k k n 1 n 1 n n
 ✓ 1 x Cn Cn x Cn x ... Cn x ... Cn x Cn x
 n 0 1 2 2 k k k n 1 n 1 n 1 n n n
 ✓ x 1 Cn Cn x Cn x ... 1 Cn x ... 1 Cn x 1 Cn x
 k n k
 ✓ Cn Cn
 ✓ Ck Ck 1 Ck 1, n 1
 n n n 1 
 k.n! n n 1 !
 ✓ k.C k nC k 1
 n n k !k! n k ! k 1 ! n 1
 1 k.n! n n 1 ! 1
 ✓ C k C k 1
 k 1 n k 1 n k !k! n 1 n k ! k 1 ! n 1 n 1
 Page 5 CHUYÊN ĐỀ VIII – TOÁN 10 – CHƯƠNG VIII – ĐẠI SỐ TỔ HỢP
 0 8 1 6 1 2 4 1 3 2 1 4 1 8 5 2 4 1
 C4 x C4 x . C4 x . 2 C4 x . 3 C4 4 x 4x 6x 4 .
 x x x x x x
 4
 1 
Câu 8. (TH) Khai triển nhị thức Newton x 2 .
 x 
 Lời giải
 4 2 3 4
 1 0 4 1 3 1 2 2 1 3 1 4 1 
 Ta có x 2 C4 x C4 x . 2 C4 x . 2 C4 x. 2 C4 2 
 x x x x x 
 0 4 1 3 1 2 2 1 3 1 4 1 4 6 4 1
 C4 x C4 x . 2 C4 x . 4 C4 x. 6 C4 8 x 4x 2 5 8 .
 x x x x x x x
 3 BÀI TẬP TRẮC NGHIỆM.
Câu 9. Trong khai triển nhị thức Niu-tơn của a b 4 có bao nhiêu số hạng?
 A. 6 . B. 3 . C. 5 . D. 4 .
 Lời giải
 Chọn C
 Trong khai triển nhị thức Niu-tơn của a b 4 có 4 1 5 số hạng.
Câu 10. Trong khai triển nhị thức Niu-tơn của 2x 3 4 có bao nhiêu số hạng?
 A. 6 . B. 3 . C. 5 . D. 4 .
 Lời giải
 Chọn C
 Trong khai triển nhị thức Niu-tơn của 2x 3 4 có 4 1 5 số hạng.
Câu 11. Trong khai triển nhị thức Niu-tơn của a b 4 , số hạng tổng quát của khai triển là
 k 1 k 5 k k 4 k k k 1 5 k k 1 k 4 k 4 k
 A. C4 a b . B. C4 a b . C. C4 a b . D. C4 a b .
 Lời giải
 Chọn B
 4 k n k k k 4 k k
 Số hạng tổng quát của khai triển a b là Cn a b C4 a b .
Câu 12. Trong khai triển nhị thức Niu-tơn của 2x 3 4 , số hạng tổng quát của khai triển là
 k k 4 k 4 k k 4 k k 4 k k 4 k k 4 k k k 4 k 4 k
 A. C4 2 3 .x . B. C4 2 3 .x .C. C4 2 3 .x .D. C4 2 3 .x .
 Lời giải
 Chọn B
 4 k 4 k k k 4 k k 4 k
 Số hạng tổng quát của khai triển 2x 3 là C4 2x 3 C4 2 3 .x .
Câu 13. Tính tổng các hệ số trong khai triển nhị thức Niu-tơn của 1 2x 4 .
 A. 1. B. 1. C. 81. D. 81.
 Lời giải
 Chọn A
 Tổng các hệ số trong khai triển nhị thức Niu-tơn của 2x 3 4 chính là giá trị của biểu thức 
 2x 3 4 tại x 1.
 Page 7 CHUYÊN ĐỀ VIII – TOÁN 10 – CHƯƠNG VIII – ĐẠI SỐ TỔ HỢP
 Hệ số của x3 trong khai triển trên ứng với k 3.
 3 4 3 3
 Vậy hệ số của x trong khai triển 1 3x là C4 . 3 108 .
 4
 1 3 
Câu 18. Tìm số hạng không chứa x trong khai triển nhị thức Niu-tơn của x .
 x 
 A. 1. B. 4 . C. 6 .D. 12.
 Lời giải
 Chọn B. 
 4 4 4 k 4
 1 3 k 1 3 k k 4k 4
 Ta có x C4 x C4 x .
 x k 0 x k 0
 Số hạng không chứa x trong khai triển trên ứng với 4k 4 0 k 1.
 4
 1 3 1
 Vậy số hạng không chứa x trong khai triển x là C4 4 .
 x 
Dạng 2. Khai triển biểu thức dạng a b 5 .
 1 PHƯƠNG PHÁP.
 =
Sử dụng công thức: a b 5 C 0 a5 C1a4b1 C 2 a3b2 C3a2b3 C 4 a1b4 C5b5
 = 5 5 5 5 5 5
 5 4 1 3 2 2 3 1 4 5
 a=I 5a b 10a b 10a b 5a b b
 2 BÀI TẬP TỰ LUẬN.
 =
 5
Câu= 1: Khai triển biểu thức a b .
 =I Lời giải
 Ta có: a b 5 a5 5a4b1 10a3b2 10a2b3 5a1b4 b5 .
Câu 2: Khai triển biểu thức (x 1)5 .
 Lời giải
 Ta có: x 1 5 x5 5x4 10x3 10x2 5x 1.
 5
Câu 3: Khai triển biểu thức x 1 .
 Lời giải
 Ta có: x 1 5 x5 5x4 10x3 10x2 5x 1.
 5
Câu 4: Khai triển biểu thức x 2 .
 Lời giải
 Page 9